《随机过程》和《随机信号分析》的研究对象和基本概念（随机过程定义）虽然完全相同，但它们从同一基本概念（随机过程定义）出发建立的布朗运动理论却完全不同，甚至相互矛盾，不能他洽（图1）。

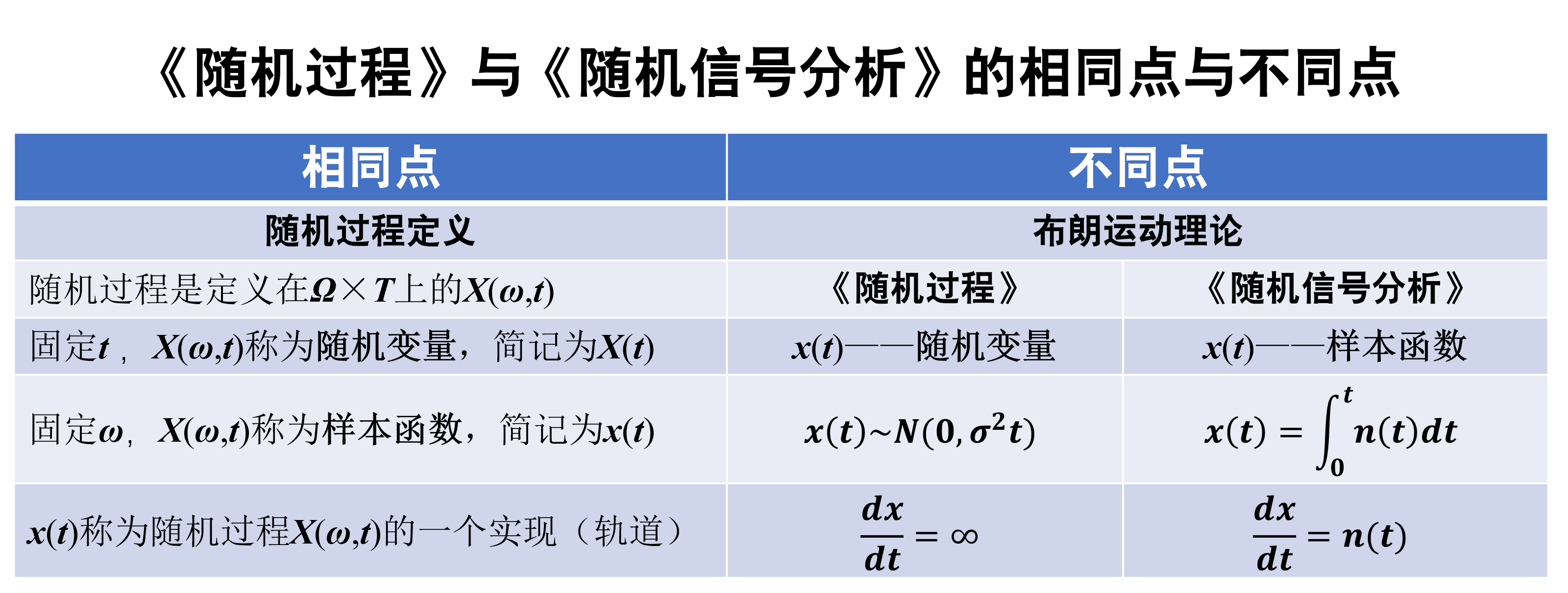
图1 《随机过程》与《随机信号分析》对比

从图1可以看出，《随机过程》布朗运动理论没有保持与“随机过程定义”中“样本函数”的概念同一，不加说明地将一个布朗粒子在t时刻的位移x(t)（一个实现）从“样本函数”替换为“随机变量”，因而产生了违反同一律的“偷换概念”逻辑错误，不仅导致《随机过程》布朗运动理论与《随机信号分析》布朗运动理论相互矛盾，而且与自然科学、工程技术和社会科学大量的布朗运动观察实验结果不符，无法正确描述实际布朗运动现象及规律。

数学史上最著名的“偷换概念”逻辑错误出现在牛顿创立的《微积分》中。牛顿在导数推导过程中违反同一律，随意用∆x=0替换∆x≠0，产生了“偷换概念”逻辑错误。

英国大主教贝克莱（Berkeley）首先发现了牛顿《微积分》中的逻辑错误（贝克莱悖论）。贝克莱严厉批评牛顿是有意识地“偷换概念”，《微积分》理论是“分明的诡辩”，并强调“逻辑错误不会产生科学”，从而引发了一场持续150多年的“第二次数学危机”，牛顿《微积分》险被推翻。

整个18世纪，数学家们的首要任务就是消除牛顿《微积分》中违反同一律的“偷换概念”逻辑错误，几乎每一位数学家都为此做出了巨大的努力。

后来柯西（Cauchy）将极限概念作为《微积分》的理论基础，才消除了牛顿违反同一律的“偷换概念”逻辑错误（贝克莱悖论），彻底解除了数学史上的第二次危机。