引用本文

段海滨, 尤灵辰, 范彦铭, 李明. 仿鸟群自推进机制的无人机集群相变控制. 自动化学报, 2025, 51(5): 960−971 doi: 10.16383/j.aas.c240598

Duan Hai-Bin, You Ling-Chen, Fan Yan-Ming, Li Ming. Phase transition control of UAV swarm based on bird-inspired self-propelled mechanism. Acta Automatica Sinica, 2025, 51(5): 960−971 doi: 10.16383/j.aas.c240598

http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c240598

关键词

无人机集群，相变控制，自组织，自推进粒子 

摘要

针对无人机集群的运动相态转换问题, 提出一种仿鸟群自推进粒子模型的无人机集群相变控制方法. 首先, 从鸟群运动行为中获得启发, 通过设计速度保持项和势能梯度项构建仿鸟群运动模型, 并设计相变控制项模拟巢穴对鸟群的吸引, 以实现集群在不同相态之间的转换. 然后, 讨论集群在设计的相变控制律作用下的运动相态, 证明无人机集群能够实现两种稳定的运动相态并进行相互转换. 最后, 仿真验证了集群存在的两种稳定运动构型, 所提出相变控制律能够实现两种集群运动相态的互相转换.

文章导读

近年来, 无人机(Unmanned aerial vehicle,UAV)集群在各个领域都受到极大的关注, 获得较大的发展[1−3]. 其中, 无人机的相变控制在无人机集群控制中已经引起一定关注[4]. 目前, 在多智能体研究领域, 相变还没有一个准确定义, 一般而言, 是指在一个集群系统中, 由于内因、外因、系统内外因相互作用等的改变, 在集群内部的相互作用调节下, 导致群体行为从一种运动模态转变为另一种运动模态的过程. 在无人机集群中引入相变控制, 能够使无人机集群适应日益复杂的任务环境, 提升集群对复杂环境的适应能力[5]. 

目前, 集群的相变控制已经成为研究的前沿领域, 学者们对不同的模型中蕴含的相变现象进行深入的讨论. Vicsek模型是一个经典的能够产生相变的模型. Xue等[6]基于Vicsek模型开展研究, 引入层级之间的控制衰减因子, 讨论衰减因子和噪声的指数临界值, 并据此研究等级机制对集群聚集带相态的影响. 相关文献则基于自推进粒子模型而非Vicsek模型, 研究三维空间中自推进粒子集群的运动过程, 并运用数值求解的方法计算集群从聚集到分散的临界参数[7]. 相比于Vicsek模型而言, 自推进粒子以自然界的鸟群运动模型为基础, 能够容纳更多类型的集群交互形式, 蕴含着更丰富的集群运动相态可能性, 因此被广泛作为多智能体相变的研究对象. Cheng等[8]研究自推进粒子在不同形式的势能项和邻居交互距离条件下集群的运动相态, 讨论不同势能作用参数下集群产生的运动相态, 并引入两种序参量来衡量集群的旋转运动和直线运动相态; 文献[9]研究集群存在通信时延的情况下集群的运动相态, 通过对集群的中心和个体相对集群中心的向量差分别进行研究, 并借助混沌学科中的分岔理论得到集群时延状态下的稳定运动相态, 探讨存在通信延迟情况下自推进粒子集群的运动规律并给出一些重要参数的解析解. 除描述不同参数下集群从初始随机状态开始所形成的运动相态, 相关文献进一步讨论某些运动相态是如何瓦解并转为另外一个相态的过程. Duan等[10]通过大量的仿真模拟, 讨论存在一个外界捕食者的情况下, 集群因为躲避而产生的涡旋到晶格运动状态的单向转变, 分析速度对齐比例系数和吸引排斥力比例系数对临界危险半径的影响. Hindes等[11]研究两个具有同样控制规律的群体从集群平移相态到集群涡旋相态的转变过程, 并研究两个群体中心距离不同对最终稳定集群状态的影响. 

自推进粒子的相变理论已经初步应用于无人机集群中. 在考虑通信延迟的集群相变的研究[9]基础上, Edwards等[12]使用虚实混合方法, 在实际的小车上测试相关理论, 验证自推进小车集群在通信延迟和集群交互强度变化时产生的不同的运动相态. Lei等[13]用小车对相变理论进行实际验证, 研究小车集群在不同的交互作用强度下不同的集群特性, 在不同的参数下测试集群一致性的收敛性和面对外界威胁时集群的反应速度. Xie等[14]研究环境中的磁场强度对微型机器人集群运动形态的影响, 并实现群体在多种形态之间的快速可逆切换. Hao等[15]则研究局部交互规则对微型机器人集群的影响, 通过改变振幅和频率, 实现对集群的聚集和分散行为的控制. 

鸟类行为是生物界中最为普遍的群体运动之一, 吸引着大量学者的研究[16−17]. 鸟群相比于其他集群运动有一个比较明显的特征, 即鸟群倾向于和邻居的速度保持一致, 这也是最经典的鸟群运动模型——Vicsek模型[18]的基本原理. 由于鸟群中存在大量个体, 对鸟群的观察和数据记录一直是相关研究的一个难点. 直到近期, 随着全球定位系统技术的进步, 人们可以通过数据比较精确地记录鸟类的位置和速度信息, 并基于相关数据为鸟群建立一系列模型, 研究集群中信息的传递[19]、信息交互机制[20]或者飞行时的轨迹形成机制[21−22]. 

总之, 目前集群相变问题已经得到广泛研究, 然而相关研究主要聚焦于集群的参数变化而导致的集群稳态解的不同, 为得到不同的集群运动相态需要调整所有个体的控制参数, 而较少考虑同一控制方程不同稳定运动相态之间的转换[8, 23]. 考虑同一方程不同相态变化的一些文献中所讨论的运动相态转变也仅局限于从涡旋态到晶格平移相态的单向转变[10], 或是某种运动相态的崩溃[24], 针对两种乃至多种稳定相态之间相互转换的研究仍然处于起步阶段. 此外, 目前相变控制理论主要针对空间中的自由粒子, 实际物理系统中应用相变理论进行控制的实例仍然较少, 目前引入相变理论的实际系统主要基于无人小车[12−13]和各种微型机器人[14, 25], 这些实际物理系统受到的硬件限制较少. 而由于无人机较为复杂的动力学特性, 基于无人机集群进行的相变仿真分析尚存在技术空白. 

基于上述情况, 本文对全连通交互拓扑下的无人机集群相变控制方法进行研究. 首先, 从鸟群飞行规律中得到启发, 基于自推进粒子模型, 考虑集群系统中的无人机满足无人机的实际飞行条件限制, 设计无人机仿鸟群相变控制律, 使无人机集群形成稳定的集群运动相态. 设计简单的相变控制项, 使无人机能够在两种不同的稳定集群运动相态中进行互相转换. 此外, 基于无人机集群仿鸟群相变控制律, 进一步分析集群的稳定运动相态, 讨论部分重要的集群运动参数, 并通过仿真验证了所设计的集群相变控制律能够实现稳定的集群平移以及涡旋运动相态. 通过调节简单的相变控制项, 集群能够在两个运动相态之间进行转换, 完成无人机集群的相变控制. 最后, 在其他社会力模型中引入相变控制项, 进行仿真对比测试, 证明了本文提出的相变控制方法更加灵活, 更适合实际无人集群的控制. 

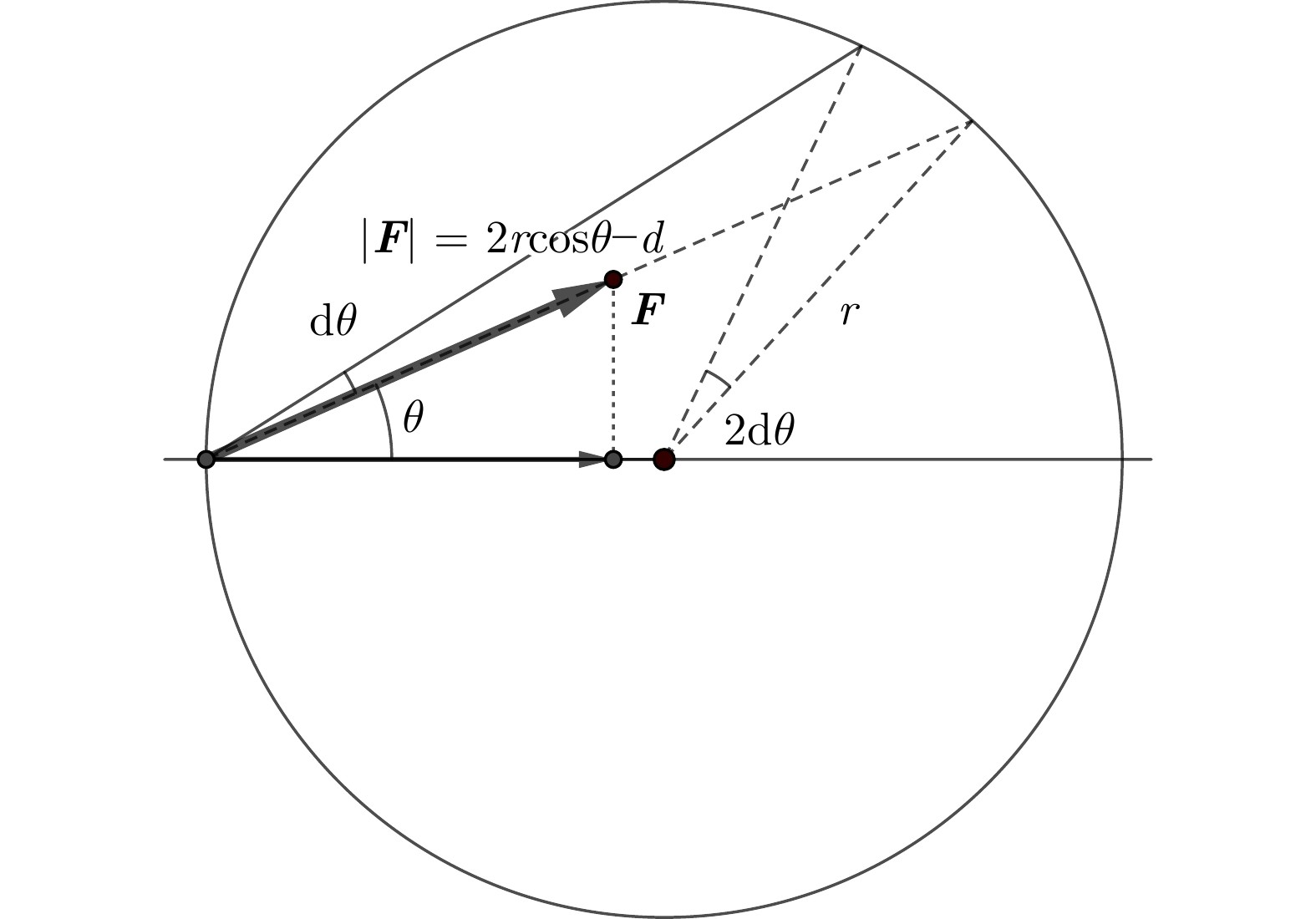
图 1  涡旋半径计算示意图

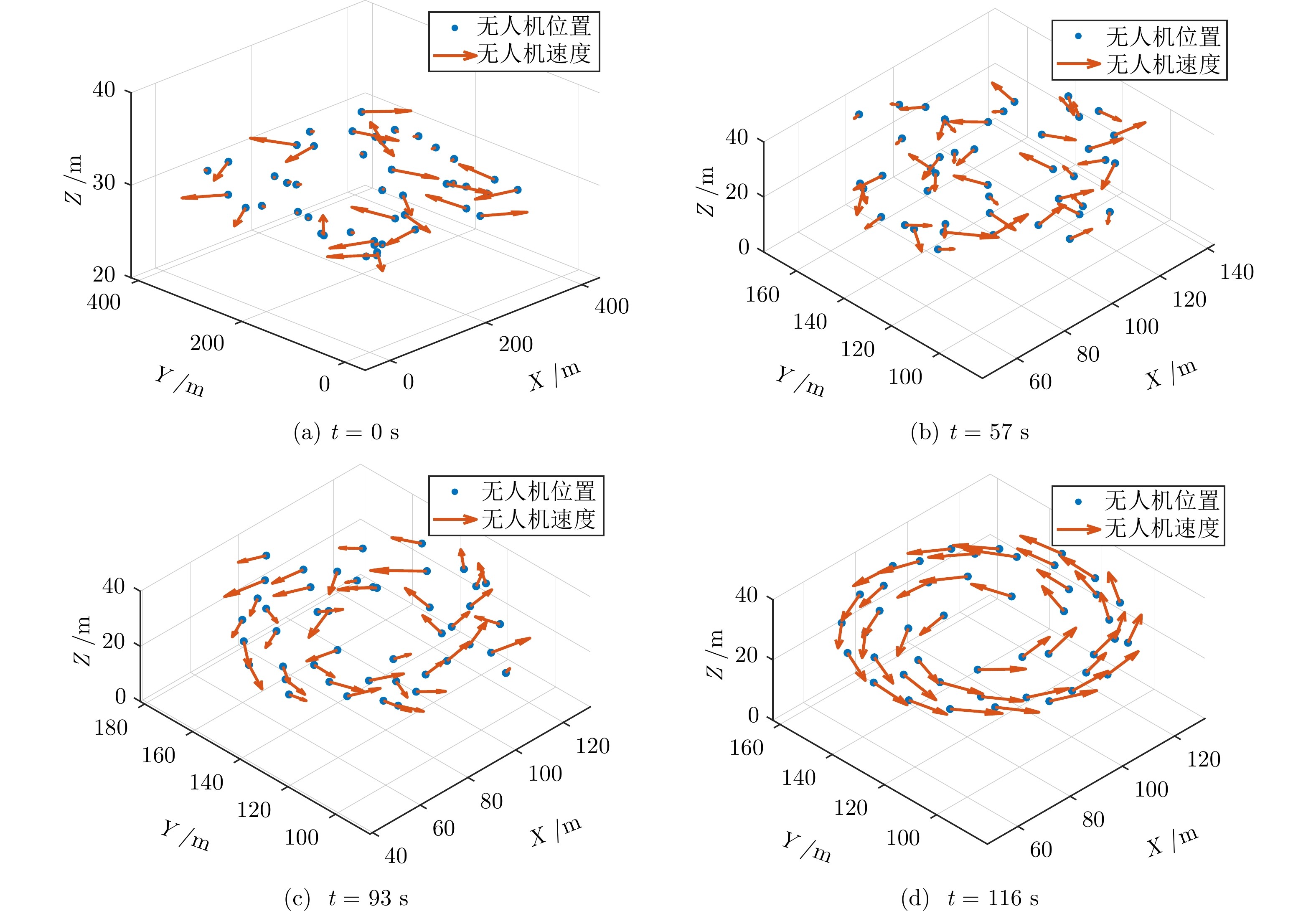
图 2  集群涡旋相态转变

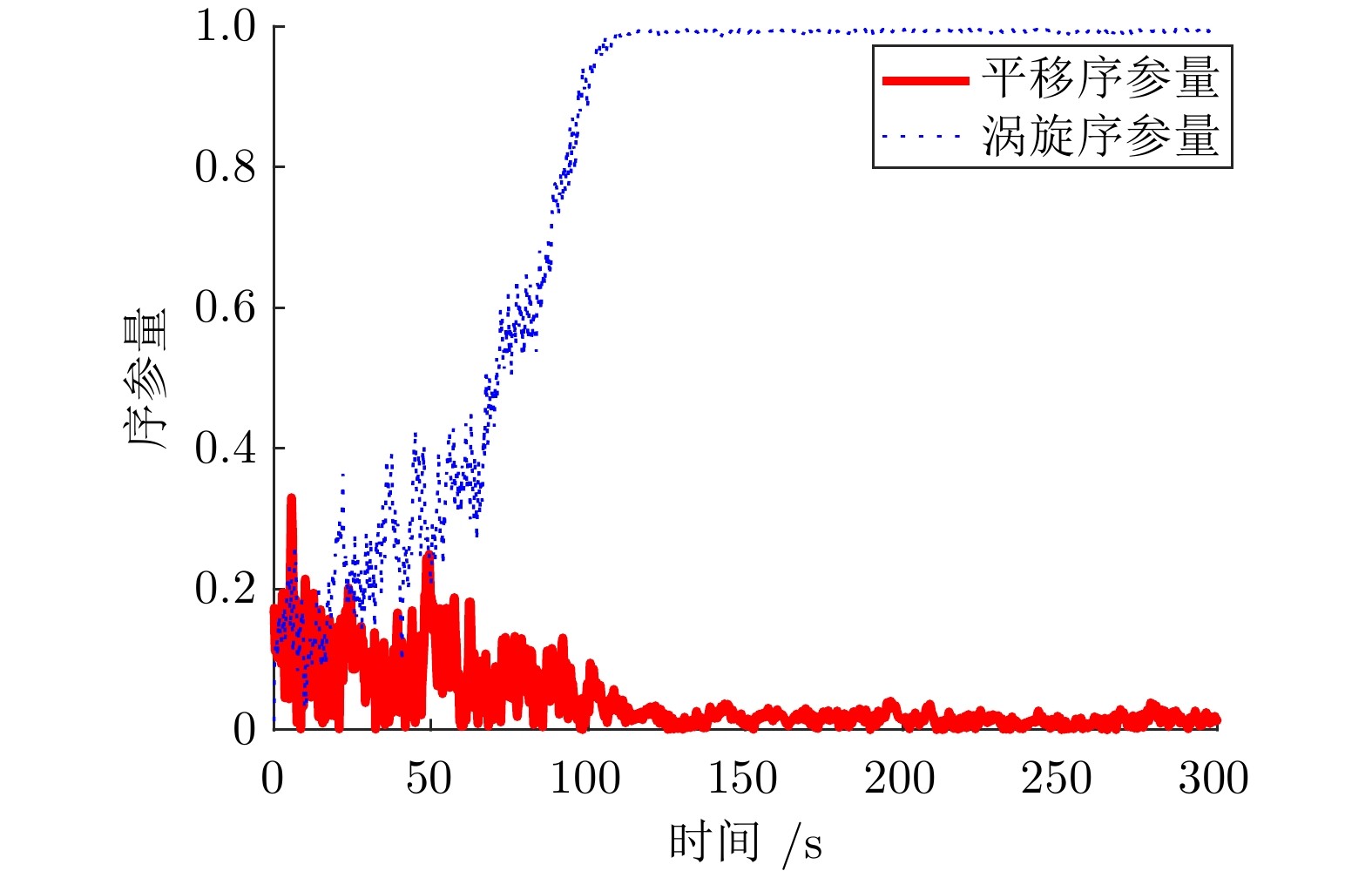
图 3  涡旋相形成过程中的序参量变化情况

本文针对自由环境中无人机集群的相变控制问题, 设计基于仿鸟群自推进粒子模型的无人机集群相变控制方法, 通过序参量指标度量无人机集群的运动一致性程度进而确定集群所处的运动相态, 实现集群在两种运动相态之间的相互转换. 根据理论证明和仿真结果得出以下结论: 

1) 受现实中鸟群运动规律的启发, 设计仿鸟群无人机集群相变控制律. 在相变控制律的作用下, 无人机集群在自组织原则的基础上能够形成两种稳定的集群运动相态, 包括平移相态和涡旋相态, 形成无人机集群稳定的一致性运动, 并分析相关相态的一些重要参数. 

2) 通过调节具有简单形式的相变控制项, 能够仅对集群中部分个体进行控制, 实现集群中两种相态的自由切换, 通过仿真验证了无人机仿鸟群相变控制律的可行性与有效性. 

作者简介

段海滨

北京航空航天大学自动化科学与电气工程学院教授. 主要研究方向为无人机集群仿生自主飞行控制. 本文通信作者. E-mail: hbduan@buaa.edu.cn

尤灵辰

北京航空航天大学自动化科学与电气工程学院博士研究生. 主要研究方向为仿生集群自主飞行控制. E-mail: lcyou@buaa.edu.cn

范彦铭

中国航空工业集团公司沈阳飞机设计研究所专业领域首席专家. 主要研究方向为先进飞行控制技术研究与系统研制. E-mail: michaelfan@yeah.net

李明

中国工程院院士, 中国航空工业集团公司沈阳飞机设计研究所首席专家. 主要研究方向为飞机自动化, 无人机自主飞行控制. E-mail: mingli@mail.sy.ln.cn