[敬请读者注意] 本人保留本文的全部著作权利。如果哪位读者使用本文所描述内容，请务必如实引用并明白注明本文出处。如果本人发现任何人擅自使用本文任何部分内容而不明白注明出处，恕本人在网上广泛公布侵权者姓名。敬请各位读者注意，谢谢！

强相关逻辑及其应用（中）

程京德 

[注：本文为笔者2016年发表在科技导报第34卷第7号上的文章“相关推论与强相关逻辑”（迄今为止唯一的一篇关于强相关逻辑的中文文献）之修改增补版，更换标题为“强相关逻辑及其应用”，发表在此。]    

    概要：推理的能力，尤其是抽象推理的能力，无疑是人类智能最本质的特征之一，因而应该是任何以实现人工通用智能为目标的人工智能系统都应该提供的必不可少的最基本功能。本文介绍构建强相关逻辑的动机，展示强相关逻辑的各种应用，并且指出，为相关推理提供逻辑有效性保证的强相关逻辑，对于以推理、发现、预测为最基本功能的各种人工智能系统来说，具有无可替代的关键作用。强相关逻辑是实现人工通用智能不可或缺的逻辑基础。

演绎论证及演绎推理的逻辑有效性标准

如前所述，“逻辑学是一门研究论证与推理之正确性的基础性学问，其目的为建立和建全用于判断各种论证与推理之正确性的一般标准。”[1] 

科学哲学中的一个观点是，科学发现中的推理过程都可以归纳为下述三种方式之一：假说-演绎、归纳-验证、以及假说生成（溯因）推理（The hypothetico-deductive account [Popper, Hempel], The inductive-probability account [Reichenbach, Salmon], and The abductive inference account [Peirce, Hanson]）[13,14]。这三种方式，恰恰对应着三种典型的论证形式：演绎、归纳、假说生成（溯因）。

在演绎、归纳、假说生成（溯因）这三种论证形式中，一个正确的演绎论证的前提中包含有一般性条件句旨在为结论提供绝对的证据支持，其结论必然来自于其前提，因此是“绝对”合理的（请注意，这里“合理”并非意味着“正确”或“真实”）。而归纳论证和假说生成（溯因）论证的前提中仅包含有特殊性陈述旨在为结论提供某种程度的证据支持，其结论并非必然来自于其前提，因此并非是“绝对”合理的而仅仅是“相对”合理的。

在逻辑学中，演绎论证及演绎推理的逻辑有效性(validity)标准，就是要为判定一个演绎论证或演绎推理是否在逻辑上正确合理提供一种评价判定准则，用于区分正确合理的演绎论证/推理和不正确合理的演绎论证/推理。接下来，让我们来看看逻辑有效性在经典数理逻辑和相关逻辑中是怎样被定义的。

在经典数理逻辑中，演绎论证的经典有效性，或者，有效性的经典解释(The Classical Account of Validity, CAV)被定义为：一个论证是（经典）有效的，当且仅当其所有前提都为真时其结论却为假是不可能的(A deductive argument is (classically) valid IF AND ONLY IF it is impossible for all the premises to be true while the conclusion is false)；或者，一个论证是（经典）有效的，当且仅当若其所有前提都为真则其结论也为真是必然的(A deductive argument is (classically) valid IF AND ONLY IF it is necessary that IF all its premises are true THEN its conclusion is true)。

经典数理逻辑是基于莱布尼兹的“普遍语言”思想为了给数学家们的工作提供形式化语言及推理规则来描述和验证数学证明而建立起来的；其主要目的是对数学证明给予严格的形式化符号化描述后进行验证（请注意，“经典数理逻辑是形式逻辑的现代化”这种说法是片面的、不完全的）。经典数理逻辑建立于四个基本假设/原理（经典抽象、弗雷格假设/可拓性原则、两值原理、经典有效性）之上，其中最基本的假设就是采用经典有效性作为论证和推理的逻辑有效性标准，从而被称为“经典”数理逻辑。

在上述演绎论证的经典有效性(CAV)之定义中有几个关键点，也是其本质上的缺陷： (1) 把前提为真结论也必为真定义为经典有效性的充分必要条件，(2) 只要结论为真就可以满足经典有效性，(3) 仅仅言及前提和结论的真假而没有对前提和结论之间是否存在有相关证据关系给予任何考虑。其中(2)及(3)都是(1)的直接后果。

让我们来看一个例子。

新西兰逻辑学家Mares曾经给出过如下的例子[15]。在1993年Wiles证明了费尔马大定理（谷山-志村猜想）之后，众多数学家都想努力对其复杂的证明加以简化。假设某位数学家到某个数论学术会议上去发表下面这样一个对费尔马大定理的简化证明：

The sky is blue 

----------------------------------------------------------------------

Therefore: There is no integer n greater than or equal to 3 such that 
   for any non-zero integers x, y, z, xⁿ = yⁿ + zⁿ. 

那么，这个简化证明当然不会被其他数学家们所认可而肯定会被嘲笑。然而，如果依据经典有效性标准，这个简化证明并没有什么问题。因为：（1）按照经典有效性标准，这个证明是有效的，其前提为真时结论不会为假（因为已知费尔马大定理成立，这里只是寻求一个简化证明）；（2）这个证明是健全的(sound)，其前提的确为真（天空是蓝的是个一般性真理）。

这样一个在数学上不可能被认可的简化证明，却可以被经典有效性标准所认可，那么显然，问题当然是在于该经典有效性标准并未提供一个合理的评价标准可以用来准确地区分正确合理的演绎论证/推理和不正确合理的演绎论证/推理，没有起到其本应起到的评价标准之作用。

相关逻辑针对数理逻辑中经典有效性标准的缺陷，增添了相关有效性(The Relevant Account of Validity, RAV)作为一个附加的有效性标准: 一个论证是（相关）有效的，其前提和结论之间必须有某种意义的联系，即某种相关性(For an argument to be (relevantly) valid, there must be some connection of meaning, i.e., some relevance, between its premises and its conclusion.)。请注意这里相关有效性(RAV)仅仅陈述了一个必要条件而非充分条件。

如果对上面的简化证明用相关有效性标准来评价判定，那么由于其前提和结论之间没有任何的意义上联系，所以就不能被认可了。

笔者修改了Mares给出的上述例子如下：

Taniyama-Shimura conjecture & The sky is blue & ……

----------------------------------------------------------------------

Therefore: There is no integer n greater than or equal to 3 such that 
   for any non-zero integers x, y, z, xⁿ = yⁿ + zⁿ. 

Taniyama-Shimura conjecture 

----------------------------------------------------------------------

Therefore: There is no integer n greater than or equal to 3 such that 
   for any non-zero integers x, y,z, xⁿ = yⁿ + zⁿ. or The sky is blue or ……

因为从Wiles证明的谷山-志村猜想可以得到费尔马大定理，所以，上面的两个证明如果用经典有效性标准及相关有效性标准来评价判定，都是应该被认可的。但是，在上面第一个证明中，前提中包含有与结论毫不相关的合取项（甚至可以有多少个！）；在上面第二个证明中，结论中包含有与前提毫不相关的析取项（甚至可以有多少个！）。这样的两个证明显然不会是数学家们可以认可的。

这样两个在数学上不可能被认可的证明，却可以被经典有效性标准及相关有效性标准所认可，那么显然，问题当然是在于经典有效性标准再加上相关有效性标准也还仍然没有提供一个合理的评价标准，它可以用来准确地区分正确合理的演绎论证/推理和不正确合理的演绎论证/推理，仍然没有起到其本应起到的评价标准之作用，仍然需要改进。

作为一个必要条件，相关有效性(RAV)仅要求“前提和结论之间必须存在有某种意义的联系”，但是并没有要求在前提中不能存在有与结论毫不相关的冗余合取项，也没有要求在结论中不能存在有与前提毫不相关的冗余析取项。所以，我们可以把相关有效性(RAV)视为/称为一种“弱”相关有效性。

相对于弱相关有效性，我们可以定义强相关有效性为：一个论证是（强相关）有效的，其前提和结论之间必须有某种意义的联系，即某种相关性，并且在前提中不存在有与结论毫不相关的冗余合取项，在结论中也不存在有与前提毫不相关的冗余析取项(For an argument to be (strongly relevantly) valid, there must be some connection of meaning, i.e., some relevance, between its premises and its conclusion; moreover, its premises include no conjuncts which are irrelevant to its conclusion and its conclusion include no disjuncts which are irrelevant to its premises.)。

基于强相关逻辑的相关推理 

让我们先来看几个简单的例子。

（1）“如果雪是白的，那么1+1=2”，
（2）“如果雪是黑的，那么1+1=2”，
（3）“如果雪是白的，那么1+1=3”，
（4）“如果雪是黑的，那么1+1=3”。

这四个以自然语言形式表达的经验条件句陈述了四个简单的论证/推理。按照我们的常识和经验，谁也不会认为这四个论证是合理的，因为在这四个论证/推理当中，无论前提与结论正确与否，从我们的常识和经验来看它们之间没有任何关联，亦即，没有任何相关关系。这样的例子当然还可以举出很多很多，它们至少向我们揭示了这样一个事实：一个论证/推理的前提和结论之间，可能不存在相关性，这样的论证/推理，不应该被视为是正确合理的。

基于这个事实，我们可以暂且把前提和结论之间具有相关性的论证/推理称为“相关的论证/推理”，而把前提和结论之间完全不具有相关性的论证/推理称为“不相关的论证/推理”。

笔者在1998年首次提出了“相关推理(relevant reasoning)”的概念并且在之后提示了相关推理在人工智能领域里的各种关键应用 [16-21]。

规范地说，一个相关推理是由若干个满足经典有效性及强相关有效性的论证所构成的序列。如果忽略中间步骤仅言及该推理的前提和结论，那么一个正确合理的相关推理的所有初始前提均为真的时候其最终结论不会为假，并且该推理的每个前提都与结论相关，在前提中不存在有与结论毫不相关的冗余合取项，在结论中也不存在有与前提毫不相关的冗余析取项。

那么，什么样的形式逻辑系统可以作为基础逻辑来支撑相关推理？或者说，什么样的形式逻辑系统所定义的逻辑有效性标准是可以用来准确地区分正确合理的相关推理和不正确合理的相关推理的？

因为经典有效性不要求论证/推理的前提和结论之间必须存在有相关关系，所以一个经典有效的论证/推理之结论未必一定是与其前提相关的，甚至可以是毫不相关的。例如，如果把上面我们举出的四个论证/推理实例放到经典数理逻辑的范围内来考察，那么除了(3)因为前提真且结论假而被视为非有效之外，其余(1),(2),(4)三个都必须被视为经典有效的！这至少向我们揭示了这样一个事实：在我们的常识和经验看来并非正确合理的论证/推理在经典数理逻辑的范围内却有可能是经典有效的，换言之，经典有效性这个逻辑有效性标准并非与我们的常识和经验中对论证/推论的正确性判断标准完全一致。经典数理逻辑显然不能支撑相关推理。

尽管基于相关性(变量共享)原理的传统的（弱）相关逻辑引入了弱相关有效性作为经典有效性的补充，但是，如同我们在上面指出的，作为一个必要条件，弱相关有效性仅要求“前提和结论之间必须存在有某种意义的联系”，但是并没有要求在前提中不能存在有与结论毫不相关的冗余合取项，也没有要求在结论中不能存在有与前提毫不相关的冗余析取项，所以就不能保证前提与结论之间的强相关性。传统的（弱）相关逻辑也不能完美地支撑相关推理。

迄今为止，可以完美地支撑相关推理的形式逻辑系统只有引入了强相关有效性概念的强相关逻辑。

相关逻辑是经典数理逻辑的保存扩张

接下来，我们陈述经典数理逻辑、相关逻辑、强相关逻辑三者之间的关系。

众所周知，经典数理逻辑是外延真值函数的逻辑，其每一个逻辑连接词都是一个外延真值函数，每一个逻辑定理都是一个恒真的外延真值函数。

从形式逻辑系统的对象语言来说，相关逻辑的对象语言引入了一个内涵原始逻辑联结词来表达必然归结(entailment)或相关蕴涵(relevant implication)，并且保留了经典数理逻辑的外延真值函数逻辑连接词。因此，相关逻辑的对象语言是经典数理逻辑的对象语言之保存扩张。

那么，经典数理逻辑的逻辑定理集合与相关逻辑的逻辑定理集合之间的关系为何呢？

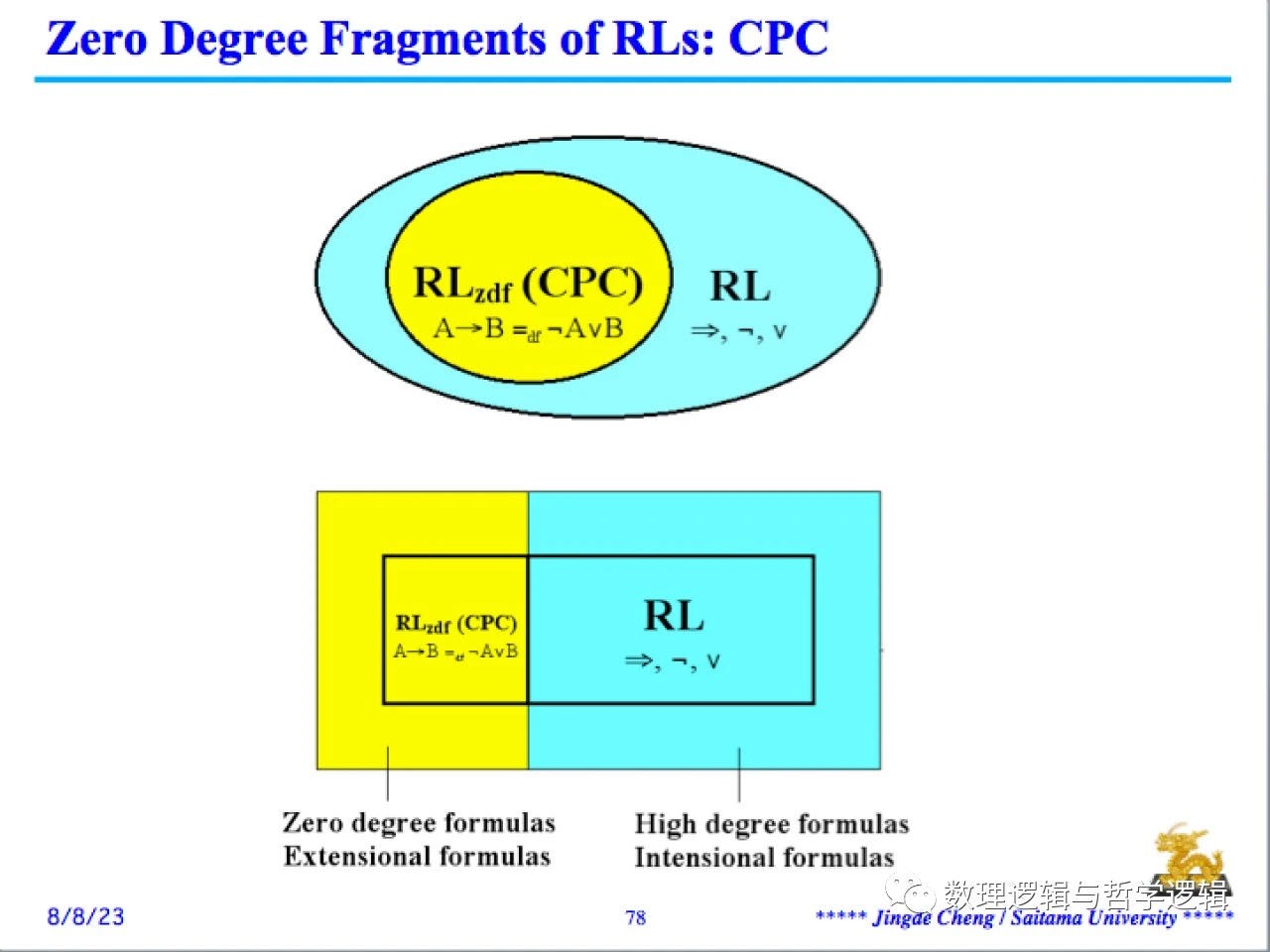
在相关逻辑中有一个元定理，Zero Degree Fragment 定理(ZDF theorem)：“在相关逻辑系统 E (R, T) 中可以证明的零度逻辑式（亦即，不含有内涵原始逻辑连接词的逻辑式）严格地都是经典数理逻辑的逻辑定理(The zero degree (i.e., includes no entailment or relevant implication) formulas provable in E (R, T) are precisely the logical theorems of CML)”[2]。因此，相关逻辑的逻辑定理是经典数理逻辑的逻辑定理之保存扩张，经典数理逻辑的逻辑定理集合是相关逻辑的逻辑定理集合的真子集。

另一方面，强相关逻辑与相关逻辑仅取内涵原始逻辑连接词及否定逻辑连接词的断片是相同的，两者之不同仅在于引入什么样的逻辑公理来刻画联言逻辑联结词与其它逻辑联结词之间的关系。因此，相关逻辑的逻辑定理是强相关逻辑的逻辑定理之保存扩张，强相关逻辑的逻辑定理集合是相关逻辑的逻辑定理集合的真子集（排除掉了相关蕴涵悖论）。

（未完待续，本文的最后部分将介绍强相关逻辑的各种应用）

参考文献

[1] 程京德, “逻辑学是什么？” 微信公众号“数理逻辑与哲学逻辑”，2023年1月25日。

[2] R. Anderson, and N. D. Belnap Jr., Entailment, “The Logic of Relevance and Necessity,” Vol. I, Princeton University Press, Princeton, 1975. 

[3] W. Kneale and M. Kneale, “The Development of Logic,” Oxford Clarendon Press, 1962, 1984 (Paperback Edition with Corrections); 中译：张家龙，洪汉鼎 译 “逻辑学的发展”，商务印书馆, 1985.  

[4] 王宪钧, “数理逻辑引论”，北京大学出版社，1982, 1998. 

[5] S. Read, “Relevant Logic: A Philosophical Examination of Inference,” Basil Blackwell, Oxford, 1988, 2012. 

[6] L. Haaparanta (Ed.), “The Development of Modern Logic,” Oxford University Press, 2009. 

[7] W. Ackermann, “Begrundung Einer Strengen Implikation,” The Journal of Symbolic Logic, Vol. 21, pp. 113-128, 1956 (in German). 

[8] J. Cheng, “Rc - A Relevant Logic for Conditional Relation Representation and Reasoning,” Proceedings of the 1st Singapore International Conference on Intelligent Systems, pp. 171-176, Singapore, September 1992. 

[9] J. Cheng, “A Relevant Logic Approach to Automated Theorem Finding,” Proceedings of the Workshop on Automated Theorem Proving attached to International Symposium on Fifth Generation Computer Systems 1994, pp. 8-15, Tokyo, Japan, December 1994. 

[10] J. Cheng, “Entailment Calculus as the Logical Basis of Automated Theorem Finding in Scientific Discovery,” in “Systematic Methods of Scientific Discovery: Papers from the 1995 Spring Symposium,” AAAI Technical Report SS-95-03, pp. 105-110, AAAI Press, March 1995.

[11] J. Cheng, “A Strong Relevant Logic Model of Epistemic Processes in Scientific Discovery,” in “Information Modeling and Knowledge Bases XI,” Frontiers in Artificial Intelligence and Applications, Vol. 61, pp. 136-159, IOS Press, February 2000. 

[12] M. R. Diaz, “Topics in the Logic of Relevance,” Philosophia Verlag, München, 1981. 

[13] M. V. Curd, “The Logic of Discovery: An Analysis of Three Approaches,” in T. Nickles (ed.), “Scientific Discovery, Logic, and Rationality,” pp. 201-219, D. Reidel, 1980. 

[14] T. Nickles, “Introductory Essay: Scientific Discovery and the Future of Philosophy of Science,” in T. Nickles (ed.), “Scientific Discovery, Logic, and Rationality,” pp. 1-59, D. Reidel, 1980. 

[15] E. D. Mares, “Relevant Logic: A Philosophical Interpretation,” Cambridge University Press, Cambridge, 2004. 

[16] J. Cheng, “Relevant Reasoning as the Logical Basis of Knowledge Engineering,” in F. J. Cantu, R. Soto, J. Liebowitz, and E. Sucar (Eds.), “Application of Advanced Information Technologies: 4th World Congress on Expert Systems, Mexico City, Mexico, March 1998,” Vol. 1, pp. 449-457, March 1998.

[17] J. Cheng, “Fuzziness and Relevance: Can We Establish a Unified Logical Basis for Approximate and Relevant Reasoning?” Proceedings of the 4th Asian Fuzzy Systems Symposium, pp. 875-880, Tsukuba, Japan, June 2000.

[18] J. Cheng, “Automated Knowledge Acquisition by Relevant Reasoning Based on Strong Relevant Logic,” in V. Palade, R. J. Howlett, and L. C. Jain (Eds.), “Knowledge-Based Intelligent Information and Engineering Systems, 7th International Conference, KES 2003, Oxford, UK, September 3-5, 2003, Proceedings, Part I,” Lecture Notes in Artificial Intelligence (Subseries of Lecture Notes in Computer Science), Vol. 2773, pp. 68-80, Springer, September 2003.

[19] J. Cheng, “Relevant Reasoning: Its Key Role in Discovery and Prediction,” in Yaoxue ZHANG, Jingde CHENG, Jianhua MA, and Zhiliang ZHU (Eds.), “Forum of Future Computing: Discussion and Prospect, International Top-level Forum on Engineering Science and Technology Development Strategy, Chinese Academy of Engineering,” pp. 197-204, Northeastern University Press, August 2013.

[20] J. Cheng, “Computing Intentions Dynamically in a Changing World by Anticipatory Relevant Reasoning,” in N. T. Nguyen, B. Attachoo, B. Trawinski, and K. Somboonviwat (Eds.), “Intelligent Information and Database Systems, 6th Asian Conference, ACIIDS 2014, Bangkok, Thailand, April 7-9, 2014, Proceedings, Part II,” Lecture Notes in Artificial Intelligence (Subseries of Lecture Notes in Computer Science), Vol. 8398, pp. 361-371, Springer, April 2014.

[21] J. Cheng, “Automated Knowledge Appreciation: A Relevant Reasoning Approach to Expand Our Knowledge and Increase Its Value Automatically,” Proceedings of the 14th IEEE International Conference on Cognitive Informatics & Cognitive Computing, pp. 175-183, Beijing, China, IEEE Computer Society Press, July 2015.

微信公众号“数理逻辑与哲学逻辑”