 精选
精选
折纸图样揭开重要物理谜团
处于粒子物理核心的一种形状——所谓振幅多面体——看起来跟折纸的数学有着深刻的联系。
Kevin Hartnett 著
左 芬 译
【译注:原文2025年10月6日刊载于QuantaMagazine,链接见文末。】
振幅多面体(Amlituhedron)是拥有近乎神秘的一个量的一种几何形状。计算它的体积,你会得到物理学中关于粒子相互作用方式的一个核心计算的答案。
如今,康乃尔大学一个名叫Pavel (Pasha) Galashin的年轻数学家发现,振幅多面体还神奇地联系到了另一个完全无关的主题:おりがみ,也就是折纸艺术。在2024年10月公布的一份证明中,他证实在折纸中出现的图样可以转变成一组点,它们共同组成了振幅多面体。不知何故,折纸的方式与粒子碰撞的方式产生了相同的几何形状。
“Pasha之前就在振幅多面体上做过一些出色的工作,”普林斯顿高等研究院物理学家,曾在2013年与自己当时的研究生Jaroslav Trnka引入振幅多面体的Nima Arkani-Hamed说道,“不过这次的工作在我看来是更高层面的。”
利用与折纸的这一全新联系,Galashin还得以解决了关于振幅多面体的一个未解猜想:这一形状可以切成更简单的构建模块,而这些模块会对应于物理学家想要执行的计算。物理学家很久以来就认定这个猜想是对的,但一直没能给出严格证明。这一猜想也可以换一种说法,那就是振幅多面体的各个片段确实按照指定的方式组装在一起。
这一成果还不仅仅在两个看起来相距遥远的研究领域之间搭建起了桥梁。Galashin与其他数学家已经在探索这座桥梁还能带给他们什么别的。他们在用它更好地理解振幅多面体——并在广泛得多的条件下解答其它问题。
爆炸式计算
物理学家想要对基本粒子相互作用时发生的情况做出预言。考虑两个叫做胶子的亚原子粒子相撞。它们可能完全不变地彼此反弹开,或是变成四个胶子,或是有其它完全不同的行为。每种结果会以一定几率发生,而这由一个叫做散射振幅的数学表达式来表征。
Feynman图被用于计算粒子碰撞产生特定结果的可能性。
数十年里,物理学家都在两种方法中选用一种来计算散射振幅。第一种使用Feynman图,也就是带有弯弯曲曲的线的一种手绘图,用来刻画粒子如何移动和相互作用。每个图代表着一个数学计算;把对应于不同Feynman图的计算加和到一起,你就能计算出一个给定的散射振幅。可是当碰撞中的粒子数增加时,你需要的Feynman图数目会爆炸式地增长。情况很快就失控了:计算相对简单的事件的散射振幅需要加和数千甚至数百万项。
第二种方法,在2000年代早期引入,被称为Britto-Cachazo-Feng-Witten(简称BCFW)递归法。它把复杂的粒子相互作用分解成更小、更简单的相互作用,从而更易于研究。你可以针对这些更简单的相互作用计算振幅,并使用顶点和边的集体也就是所谓图来追踪它们。这些图告诉你如何将简单些的相互作用缝合回去,从而计算出原始碰撞的散射振幅。
这些图追踪着复杂的BCFW递归公式。
BCFW递归法比Feynman图花的工夫要少。它不再需要加和数百万项,可能只需要加和数百项。不过两种方法都有同样的问题:最终的答案往往比繁复的计算过程简单得多,因为许多项最后都抵消掉了。
紧接着,2013年,Arkani-Hamed 和Trnka做出了一个惊人的发现:粒子碰撞的复杂数学实际上是伪装起来的几何。
几何营救
2000年代早期的时候,麻省理工学院数学家Alexander Postnikov正研究被称为正Grassman空间的一种几何对象。
正Grassman空间自1930年代起就是数学家很感兴趣的一个主题,它需要以一种高度抽象的方式来构建。首先,取一个-维空间并考虑处在其中的具有某个给定的较小维度的所有平面。例如,在我们生活的三维空间里,你可以找到在每个方向上延伸着的无穷多个二维平面。
每个平面——本质上是更大的-维空间的一个切片——可以用一个数字的阵列亦即矩阵来定义。你可以从这个矩阵计算出某些数值来,也就是所谓余子式,它们会告诉你关于该平面的一些性质。
Pavel Galashin开发出了折纸与粒子物理之间的联系。
现在只考虑你的空间里余子式全都为正的那些平面。所有这种特殊的“正”平面的集体组成了一个复杂的几何空间——正Grassman空间。
为了理解正Grassman空间丰富的内在结构,数学家把它拆分成不同的区域,使得每个区域由一批共享特定模式的平面组成。Postnikov希望把这一任务简单化,就想出了一种办法来追踪不同的区域以及它们的组合方式。他发明了所谓的平双(“平面双色”的简称)图——也就是由黑点和白点组成的网络,黑白点之间有边连接,并且这些边画出来时不会交叉。每个平双图刻画正Grassman空间的一个区域,从而给予了数学家一种视觉语言来描述本来是用繁复的数学公式定义的对象。
在Postnikov引入他的平双图近十年后,Arkani-Hamed与Trnka开始试着计算各种粒子碰撞的散射振幅。他们在应对BCFW递归公式的时候,注意到了一个离奇的事情。他们用来追踪计算的图看起来就像Postnikov的平双图。他们很好奇,于是开车前往MIT与他会面。
“午餐时我们得出结论,‘太神奇了,我们看到的完全是同一种事物,’”Arkani-Hamed回忆道。
他们是对的。为了计算个粒子碰撞的散射振幅,物理学家得加和许多BCFW项——而这些项中的每一个都对应于
维里的正Grassman空间的一个区域。
Arkani-Hamed和Trnka意识到这一几何关联可能会让散射振幅的计算更容易一些。使用粒子的碰撞数据——例如粒子的动量——他们定义了正Grassman空间的一个低维阴影。这一阴影的总体积就等于散射振幅。
于是振幅多面体就这样诞生了。
涉及八个胶子的粒子碰撞对应的振幅多面体的图示。
这还仅仅只是故事的开头。比如,物理学家和数学家想要确认,定义正Grassman空间各个区域的平双图同样也定义了振幅多面体的片段——并且这些片段不会有间隙或是重叠,从而完美地组合出其精确体积。这一期望逐渐被称为三角剖分猜想:振幅多面体是否能明白无误地三角剖分或者说细分成更简单的构建模块?
证明这一点将确立Arkani-Hamed与Trnka的远见:得出粒子碰撞散射振幅的复杂BCFW公式可以理解为振幅多面体的各个构建模块的体积之和。
这可不容易。首先,一开始就很清楚其实有两种振幅多面体。第一种定义使用的是动量-扭量坐标——一种巧妙的数学重标记,使得该形状更易于处理,因为它跟正Grassman空间以及Postnikov的平双图自然地关联着。数学家在2021年设法证明出了针对这一版本的振幅多面体的三角剖分猜想。
另一个版本,也就是所谓动量振幅多面体,则是直接用对撞粒子的动量来定义的。物理学家更关心这第二个版本,因为它跟实际粒子碰撞以及散射振幅使用的是相同的语言。结果,这一三角剖分猜想还完全未解。
如果三角剖分对动量振幅多面体会失效,那么它将意味振幅多面体并不能作为合适的方式来理解BCFW公式对散射振幅的计算。
十多年过去了,这一不确定性依然延续——直到对折纸的研究开始指出一条前行之路。
寻找大脚怪
Pavel Galashin最开始想要研究的既不是折纸,也不是振幅多面体。2018年,作为Postnikov的研究生之一,他和一个同行刚刚开始证明正Grassman空间与Ising模型之间的一种迷人的关联。Ising模型是用来研究铁磁体这类体系的行为的。Galashin试图用正Grassman空间来理解关于Ising模型的一个著名证明,尤其是它所展现的特殊对称性。
在处理证明的过程中——在之后数年里他间歇性地回到这一主题上——Galashin发现了几篇有趣的文章,研究者在其中使用了其它种类的图来使得几何更易于处理,也就是折纸的折痕图样。这些就是一些线条图,告诉你在哪里把纸折起来,来得到比如说一只仙鹤或者青蛙。
这一折痕图样生成了一只天鹅。
可能有些奇怪,折纸怎么会在这里突然冒出来了。不过在这些年里,折纸的数学已经变得惊人地深奥。关于折纸的问题——例如,一个给定的折痕图样是否会生成一个无需撕破就可展平的形状——在计算上是难以解决的。并且如今人们已经知晓折纸可以用来执行所有种类的计算。
2023年,在探究折纸在Ising模型相关的文章中起到的作用时,Galashin遇到了一个问题,并给予了关注。假定你只知道折痕图样的外边界——纸的边界,在那里折痕分为多条线段——的信息。更具体一点,假定你只知道折前和折后这些线段在空间中排布方式的信息。你是否总能找到一个完整的折痕图样,它既满足这些约束,又能生成一个可适当展平的折纸形状?数学家猜想答案是肯定的,但是没人能证明它。
Galashin觉得这一猜想很惊人,因为在他的常规研究领域也就是正Grassman空间里,检查一个对象的边界是从其获取信息的常用方法。
Jaroslav Trnka(左)与Nima Arkani-Hamed引入了振幅多面体,从而使粒子物理中的重要计算更易于执行。
可是在几个月里,他没能在这上面取得进展。接着他突然顿悟了:这个问题并不刚好跟他自己的研究路线气味相投。它可以重写成振幅多面体。并且是动量振幅多面体。
“这花费了我很长时间,我都不好意思说了,”他说道,“你不曾预期这种联系,所以你怎么也认识不到它。你不会想到在曼哈顿会发现大脚怪。”
可是他能证明它吗?
忘记平性
Galashin考虑涉及一定数目粒子的碰撞,并从分为同样数目线段的折痕图样边界出发。
他用两个数字组成的一个矢量来描述每条线段。接下来,他写出在折叠后描述这些相同线段的新位置的矢量。这些是基于他感兴趣的碰撞中关于粒子动量的信息而确定下来的。
对于每条线段,他接着把“前”与“后”矢量结合成单个四维矢量。把所有这些矢量中的数字列为一组坐标,Galashin得以在一个高维空间中定义一个点。而这个点并不会只是处在高维空间中的任意位置——它会位于动量振幅多面体内。
Galashin证明,平叠折痕图样的折纸问题确实具有肯定的答案——并且对于给定边界,一旦这样一种折痕图样被找到,其边界蕴涵的点一定处在振幅多面体内。
这是思考这一形状的一种全新方式。“与折纸的这一联系给了你动量振幅多面体的一种超级美妙的单行定义。这是Pasha的工作里让我感到最神奇的地方。”Arkani-Hamed称。
Galashin基于折纸的新诠释给他提供了一种思路去最终解决动量振幅多面体的核心谜团。如果他可以证明每个折纸导出的点不仅位于振幅多面体内部,还在一个非常特殊的区域内部——刚好使得这些区域会严丝合缝地榫接在一起——那么他就可以解决三角剖分猜想。
为此,他开发了一个算法,以边界图样为输入,并为其指派一种独一无二的折痕图样。这一折痕图样始终会遵从将其关联到振幅多面体几何的规则:也就是说,当折叠后,纸仍然可以展平。
Galashin接着用平双图来表示折痕图样:首先,他在折痕图样每个区域的中间画一个点,如果该区域在纸张折叠后朝上则将其着为白色,而如果它朝下则着为黑色。接着他在共享折痕的区域的点之间画一条边。
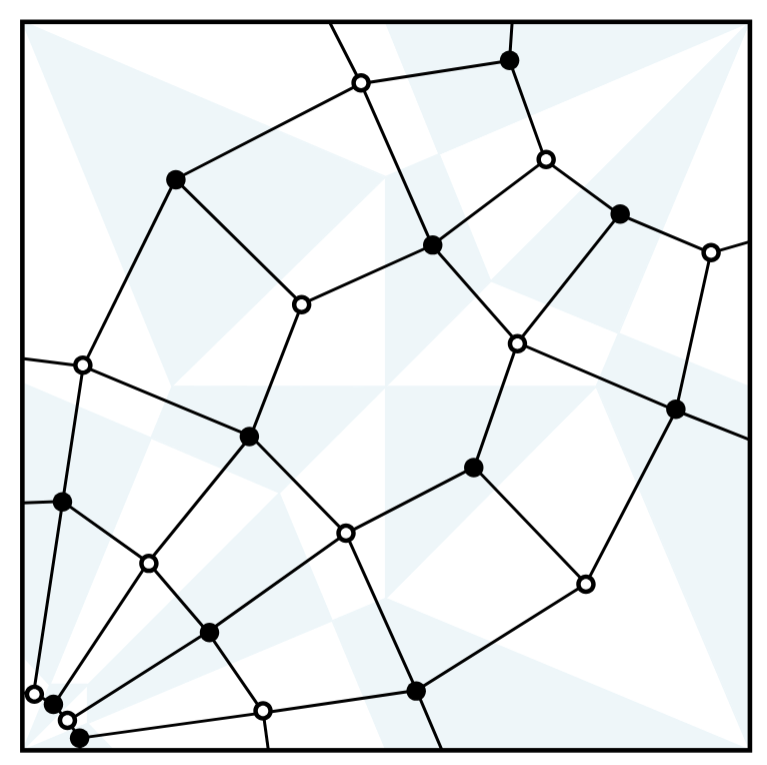
这个平双图中的边连接共享折痕的区域。
最后,他证明这个图在振幅多面体中开辟出一个区域来。而折痕图样的边界所蕴涵的点处在这个区域内部。
这就足以解决三角剖分问题了。如果振幅多面体的两个区域重叠——也就是说,振幅多面体中的一个点处在两个不同区域中——这就等价于可以将一个边界图样匹配到两个不同的折痕图样。可是Galashin的算法已经设计成只产生唯一的匹配,因此这是不可能的。类似地,该算法也意味着不存在间隙:振幅多面体中的每个点都可以重写为一个边界,而每个边界,当输入到算法中时,都会整齐地落入到一个区域内。
振幅多面体完美地拼合起来了。
全新梦想
在数学家看来,这一论证的优雅令人震撼。
“能将两种看起来毫无关联的想法联系起来往往会相当优美,”哈佛大学数学家Lauren Williams说道,“我之前没有想过折纸的折痕图样,所以看到它们跟振幅多面体相关联非常惊讶。”
Galashin也跟她一样惊讶。“折纸边界为什么会是振幅多面体中的点,对此我也没有很好的解释,”他说,“没什么先天的理由一者为何跟另一者有关。”不过他希望未来的探索会揭晓这一关联的深层理由。
他也希望他的结果能帮助他实现最初的目标:通过正Grassman空间的棱镜来理解铁磁模型以及相关体系。或许折纸也能有所帮助。
更一般地,物理学家和数学家想要看看他们能否借助折纸的视角来进一步学习振幅多面体——并将其运用在更多种关于粒子碰撞的理论计算中。例如,一个目标是通过振幅多面体的体积直接计算散射振幅,而无需将其分解成片段。或许继续探索折痕图样与粒子碰撞的关联会有助于实现这一梦想。
“作为一个物理学家,我一百万年也想不出这种方法,”Arkani-Hamed说,“不过我觉得它是一个辉煌的成果,我想进一步弄懂它,看看它会告诉我们什么。”
原文链接:
https://www.quantamagazine.org/origami-patterns-solve-a-major-physics-riddle-20251006/
转载本文请联系原作者获取授权,同时请注明本文来自左芬科学网博客。
链接地址:https://wap.sciencenet.cn/blog-863936-1506410.html?mobile=1
收藏

