 精选
精选
一种度量扭结的简单办法土崩瓦解
两位数学家证明,一个直截了当的问题——解开一个扭结有多难?——拥有相当复杂的答案。
Leila Sloman 撰文
左 芬 翻译
【译注:原文2025年9月22日刊载于QuantaMagazine,链接见文末。】
1876年,Peter Guthrie Tait 打算度量扭结的一个量,他称之为扭结度(“beknottedness”)。
这位苏格兰数学家的研究后来为现代扭结理论奠定了基础。当时他试图找到一种办法来区分扭结——一个众所周知的艰巨任务。在数学里,扭结指的是一根缠绕起来的弦,并且两个端点粘在一起。如果你能通过扭曲和拉伸但不切断弦来把一个扭结变成另一个,这两个扭结就被视为相同。但光是基于扭结的形状,很难判断这是不是可行的。例如,一个扭结看起来缠绕得相当复杂,但实际上可能等同于一个简单的圈。
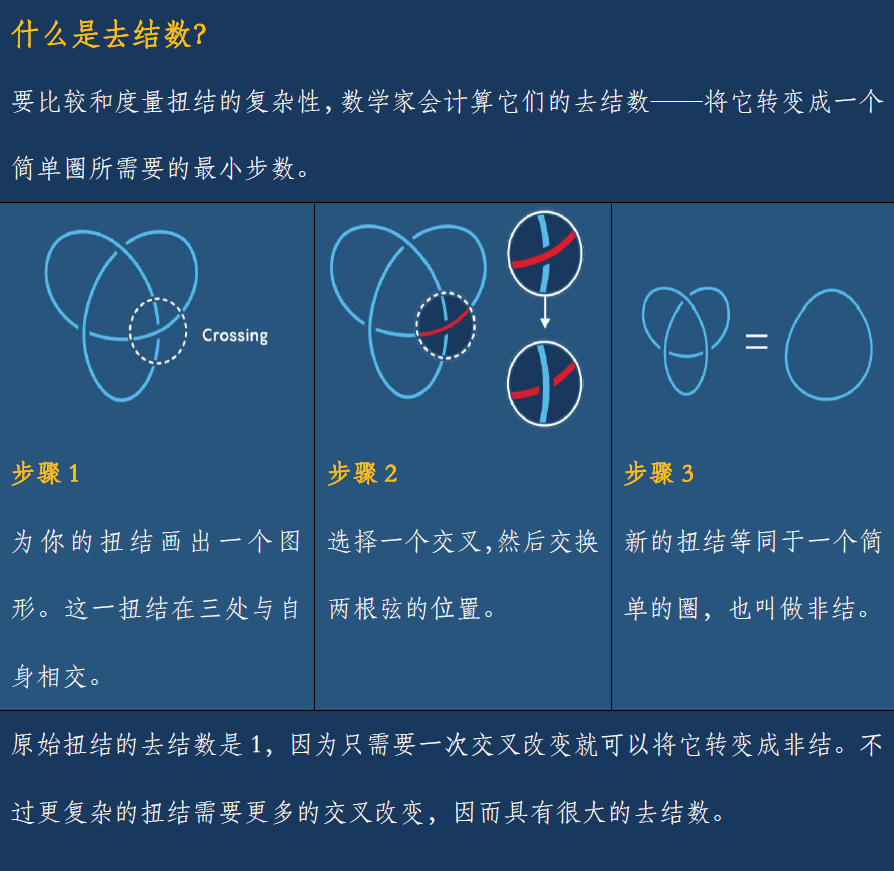
Tait想到了一个方法来判断两个扭结是否不同。首先,把一个扭结展平在桌子上,并且找出弦与自身相交的点。剪断弦,交换两根弦的位置,然后重新粘接起来。这被称为交叉改变。如果你这么做了足够多次,你会得到一个没打结的圈。Tait的扭结度就是这一过程所需要的交叉改变的最小数目。如今,它被称为扭结的“去结数”(unknotting number)。
如果两个扭结拥有不同的去结数,那么它们必然不同。不过Tait发现他的去结数带来的问题比解答的更多。
“我完全沉浸在一种兴奋状态中,”在给朋友,科学家James Clerk Maxwell,的一封信中他写道,“以致我都担心我可能遗漏了或是在过度吹捧其他人看起来极其简单的一些东西。”
如果说Tait遗漏了什么东西,那么追随他的每个数学家也都一样。在过去的150年里,许多扭结理论家都被去结数难倒了。他们清楚它可以为扭结提供一种强有力的刻画。“可以说,它是所有度量中最基础的,”内布拉斯加大学的Susan Hermiller说道。不过计算一个扭结的去结数往往出奇地难,并且它跟扭结的复杂性如何对应并不总是很清楚。
苏格兰物理学家及数学家Peter Guthrie Tait 开创了对扭结分类的系统性研究。扭结分类后来成为扭结理论中最重大的问题之一。
为了解开这一谜团,数学家们在20世纪早期构想出了一个直截了当的猜想,来说明扭结在拼接起来时去结数是怎么变化的。如果能证明这一猜想,他们就有办法对任何扭结计算出去结数——从而给予数学家一种简单而具体的方法度量扭结的复杂性。
研究者们搜索了接近一个世纪,也没找到什么证据来支持或反驳这一猜想。
接着,在今年六月份公布的一篇文章中,Hermiller和她的长期合作者Mark Brittenham发现了一对扭结,它们拼接起来形成的新扭结比猜想的预言更容易解开。基于此,他们证否了这一猜想——并且使用他们的反例发现了无穷多对可以证否它的其它扭结。
“当文章公布出来时,我都喘不过气来了,”弗吉尼亚联邦大学的Allison Moore说道。
这一结果表明“去结数是混沌且不可预测的,研究起来更加激动人心,”她补充道。这篇文章“就像是在挥舞着一面旗子,上面写着‘我们并没有真正理解这个’。”
去结与最大的未知
这一猜想至少可以追溯到1937年,当时德国数学家Hilmar Wendt打算弄清当你把扭结拼接起来时会发生什么——也就是说,在粘接扭结的端点之前,直接把它们连成一根弦。(数学家把这一拼接起来的扭结称为“连通和”。)Wendt认为最终扭结的去结数应该总会是两个初始扭结的去结数之和。
他的预测,如果被称为可加性猜想,是有道理的。比方说你把上面的两个扭结拼起来,它们各自的去结数已知分别是2和3。这意味着,对连通和左边的扭结依次做2次交叉改变就可以去结,对右边依次做3次交叉改变就可以去结。如果你使用这些操作序列,就可以把整体在2+3也就是5次交叉改变下解开。
可是这只会告诉你连通和的去结数不会大于5。你或许能找到一个交叉改变的序列,比两侧单独解结要更高效。也就是说,可能存在一个扭结,它的去结数比其局部之和更小。
“我们几乎放下了其它任何事情。所有生活都不复存在。吃饭、睡觉也变得烦人。” —— Susan Hermiller
为了解决可加性猜想,数学家们要么就得找到一个去结序列更短的连通和,要么就得证明这样的实例不存在。不管是哪种情况,他们都有些无从下手。
问题的部分原因在于,你展示扭结的方式——也就是数学家所谓的“图形”——决定了扭结在何处以及如何与自身交叉。有大量的图形会代表同一个扭结。要找出交叉改变的最短序列,你可能必须选择一个恰当的图形。往往,它并不是你通常联系到该扭结的那个图形。
“在你决定引入交叉改变之前,可以想出多到难以想象的方式去尝试改变你的图形,”Brittenham说道,“至少在刚开始,我们对这一局面到底有多复杂完全没有任何控制。”
1985年,数学家Martin Scharlemann终于取得了一些进展,证明对于去结数为1的任何两个扭结,其连通和总是具有去结数2。“这使得【整个猜想】似乎变得大有可能了,”印第安纳大学的Charles Livingston说道。
Susan Hermiller(左)与Mark Brittenham证否了关于扭结的一个数十年之久的猜想,从而让数学家们对这些看似简单的对象的理解陷入困境。
这一结果为扭结世界有可能整齐而有序提供了诱人的证据。这是因为,所有扭结都可以用更小一类的“素”扭结构造出来。可加性猜想意味着一旦你知晓这些素扭结的去结数,你就知道了所有扭结的。对给定扭结你想要知道的任何信息都会自然地归结到这一简单得多的集合。
数学家希望这一猜想成立,墨尔本大学的Arunima Ray说道,“因为这就好比是,在这个世界里存在着秩序。”
Scharlemann的结果后来被推广到其它种类的扭结。不过尚不清楚它是否能应用到所有扭结。
接着Brittenham和Hermiller收集了一批电脑来帮忙。
步行网络
两人十年前就开启了他们的项目,并定下了一个宏大的目标:用计算机来获取任何关于去结数的可能结果。
他们求助于一个名为SnapPy的软件,它使用精良的几何技术来检测两个图形是否刻画同一个扭结。就在几年前,SnapPy大幅扩展了它的数据库,使得它可以识别接近60000个独特的扭结。
这个软件完美地适配Brittenham和Hermiller的意图。他们从单个复杂的扭结出发,对它应用每种想象得到的交叉改变,来产生大量的新扭结。接着他们用SnapPy来识别这些扭结——并重复这一过程。
他们对对应于数十万个扭结的数百万个图形执行了这样的操作。最终,他们汇总了一个关于去结序列的超级库,并计算出了数千个扭结的去结数的上界。这一任务需要大量的算力:两人在内布拉斯加大学申请了超算机时,同时也用他们在拍卖市场买到的旧电脑来跑程序。总之,他们弄到了数十台计算机。“我们有了一个小的步行网络,”Brittenham说道,“靠人从一台计算机步行到另一台计算机来传输信息。”

Tait罗列出了大量扭结,并记录下了它们的性质。这一页摘自1885年的一篇论文。
二人组在后台运行了他们的程序超过十年。在这段时间里,他们的杂牌军里有两台电脑倒下了,因为过热甚至产生了火花。“有一台确实冒出了火花,”Brittenham说道,“这有点滑稽。”(这些机器全都“荣休”了,他补充道。)
接下来,2024年秋天,一篇使用机器学习来证否可加性猜想但失败了的文章引起了Brittenham和Hermiller的注意。他们觉得,机器学习或许并非解决这一特定问题的最佳方法:如果确实有一个可加性猜想的反例在那,它会是“干草堆里的一根针”,Hermiller说道,“这不像是机器学习能做到的事。它们都是试图在事物中找到模式。”
不过这加强了两人一直拥有的信念——或许他们精心训练的步行网络能找到那根针。
骨肉相连
Brittenham和Hermiller意识到,他们可以使用之前发现的去结序列来搜索可加性猜想的潜在反例。
再次设想一下,你有两个扭结,它们的去结数分别是2和3,然后你试图解开它们的连通和。经过一次交叉改变,你得到了一个新扭结。如果可加性猜想成立的话,那么原始扭结的去结数应该是5,而这个新扭结的则应该是4 。
可是如果这一新扭结的去结数已经知道是3了呢?这意味着原始扭结可以在仅仅4步内解开,从而推翻了猜想。
“我们得到了这些中间扭结,”Brittenham说道,“我们从它们能得出什么呢?”
对于这一情况他和Hermiller已经拥有了完美的工具,正忙活在他们那一组电脑上呢:他们在过去十年里发展起来的数据库,里面有着数千个扭结的去结数上界。
“当文章公布出来时,我都喘不过气来了。”
—— Allison Moore
两位数学家开始拼接扭结对,并操作它们连通和的去结序列。他们聚焦于这类连通和,它们的去结数还只近似到最宽泛的程度,因而在最大与最小可能值之间有着很大的空隙。不过这仍然留下了一长串的扭结要处理——“肯定有几千万个,甚至可能有上亿个,”Brittenham说。
在几个月里,他们的电脑程序都在对这些扭结执行交叉改变,并将得到的扭结与数据库里的那些进行比较。晚春的一天早晨,Brittenham像往常很多天一样去检查程序的输出文件,看有没有什么有趣的结果出现。让他大吃一惊的是,屏幕上出现了一行文本:“连通和破坏”。这是他和Hermiller编在程序里的一条消息——但从未期待能真正看到它。
刚开始,他们对这一结果有些怀疑。“在我们脑海里首先想到的是,我们的程序有什么地方出错了,”Brittenham说。
“我们几乎放下了其它任何事情,”Hermiller回想道,“所有生活都不复存在。吃饭、睡觉也变得烦人。”
然而他们的程序通过了核验。他们甚至把它识别的扭结用绳子编出来了,并手动执行了去结过程,以便确认。
他们的反例真实存在。
盘根错节
Brittenham和Hermiller发现的反例是由所谓(2,7)环面扭结的两个副本拼起来的。这一扭结将两根弦相互缠绕三圈半,然后把相反的端粘合起来。它的镜像则是朝另一个方向缠绕三圈半得到的。
(2,7)环面扭结和它的镜像的去结数都是3。可是Brittenham和Hermiller的程序发现,如果你拼接起这俩扭结,只需要五步就可以解开其整体——并非可加性猜想所预言的六步。
“这是个出奇简单的反例,”Moore说道,“它起源于交叉改变的不可预言性。”
这一结果引导Brittenham和Hermiller得出了一个无穷序列的其它反例,其中包括几乎所有通过缠绕两根弦并粘接得到的扭结。
这样一来,可加性猜想就被决定性地推翻了,也让扭结理论界有了更广阔的探索空间。
对于某些数学家而言,这一全新结果带来的是失望。它揭示出,在扭结世界里存在的结构比他们希望得到的要少。去结数“表现得不尽如人意,”Ray说道,“这有点可惜。”
可是从另一个视角来看,这只会让去结数更加引人入胜。“比起我们几个月前的认知来说,扭结理论里其实存在着更大的复杂性和更多的未知。”Livingston称。
这一额外复杂性的本质仍不清楚。在他们对反例的粗暴检查中,Brittenham和Hermiller没能发展出一种直觉,来解释为何这些反例会违背可加性猜想,而其它扭结则不会。理解这一点能帮助数学家更好地掌握让一些扭结复杂而另一些简单的原因。
“我依然被去结数这一最基本的问题困扰着,”Moore说道,“新结果不过是在鲜花着锦、烈火烹油罢了。”
原文链接:
https://www.quantamagazine.org/a-simple-way-to-measure-knots-has-come-unraveled-20250922/
转载本文请联系原作者获取授权,同时请注明本文来自左芬科学网博客。
链接地址:https://wap.sciencenet.cn/blog-863936-1503736.html?mobile=1
收藏

