数学家证明126维包含奇特扭曲形状

关于特定维度中反常形状的长达65年的故事在全新证明中迎来高潮。

Erica Klarreich 著

左   芬      译

【译注：原文2025年5月5日刊载于QuantaMagazine，链接见文末。】

将三维空间中的直觉照搬到高维王国里看上去很诱人。毕竟，添加又一个维度只是长出了一个新的方向，可以在其中盘桓。这并不改变空间的定义性质：无边性与均匀性。

但不同的维度有着截然不同的个性。在8维和24维里，可以将球异常紧密地堆积在一起。在其它维度里，存在“奇异”的球，它们看上去皱得不可救药。而维度3是唯一能容纳扭结的——在任何更高的维度，哪怕你把结的末端牢牢地固定住，也可以把它解开。

如今，在一个诞生至今已经65年之久的维度怪异性故事上，数学家们终于迎来了结局。数十年来，研究者们一直想知晓哪些维度可以容纳某种特定的奇怪形状——它们极度扭曲以致无法通过一个被称为“手术”的简单过程转变成球面。数学家们已经证明，这些形状的存在与拓扑学中不同维度球面之间的关系这种基本问题紧密纠缠在一起。

经过这些年，数学家发现这种扭曲形状在2,6,14,30和62维中存在。他们还证明这类形状不可能在任何其它维度中存在——但有一个例外。没人能确定126维的状况。

三位数学家如今解决了这一遗留问题。在去年12月在线公布的一篇文章中，复旦大学的林伟南、王国祯与加州大学洛杉矶分校的徐宙利证明126其实也是能容纳这些奇特扭曲形状的几个罕见维度之一。

这是“一个漫长的工程，最终完工了，”牛津大学数学家、Isaac Newton数学科学研究所所长Ulrike Tillmann称。

将计算机计算与理论洞见结合起来的这一证明，“称得上一项丰碑式的工程项目，”哈佛大学的Michael Hopkins说道，“他们的做法简直让人惊掉了下巴。”

末日猜想

1950年代，数学家John Milnor证明维度7可以容纳“奇异”的球面，一举震惊了数学界。一个奇异球面从拓扑的视角来看跟普通球面毫无二致，因为拓扑学只考虑一种形状在拉伸和变形时不改变的那些性质。可是这两种球面有不相容的光滑性定义——在常规球面上光滑的一条曲线放到奇异球面上可能就不被看作光滑的了。Milnor渴望探索并分类这些奇异的球面，它们在某些维度里很少见，但在其它维度里则数以千计。

为了实现这个，他引入了一种叫“手术”的技术。这是一种可控的方法，用来化简一个数学形状或者说流形，并有望将其转变成奇异球面。它后来成为了更一般地研究流形的必备方法。

如同其名所示，手术需要切除流形的一个片段，然后沿着切割的边缘缝合上一个或多个新的片段，并且不产生尖的角落或者边缘。（当谈到关于扭曲形状的问题时，数学家还要求手术遵从流形的“标架”，也就是关于流形如何放置在空间中的一种技术属性。）

为了看出这一过程是如何执行的，我们来用手术将一个环面（甜甜圈的二维表面）转变成一个球面（球的二维表面）：

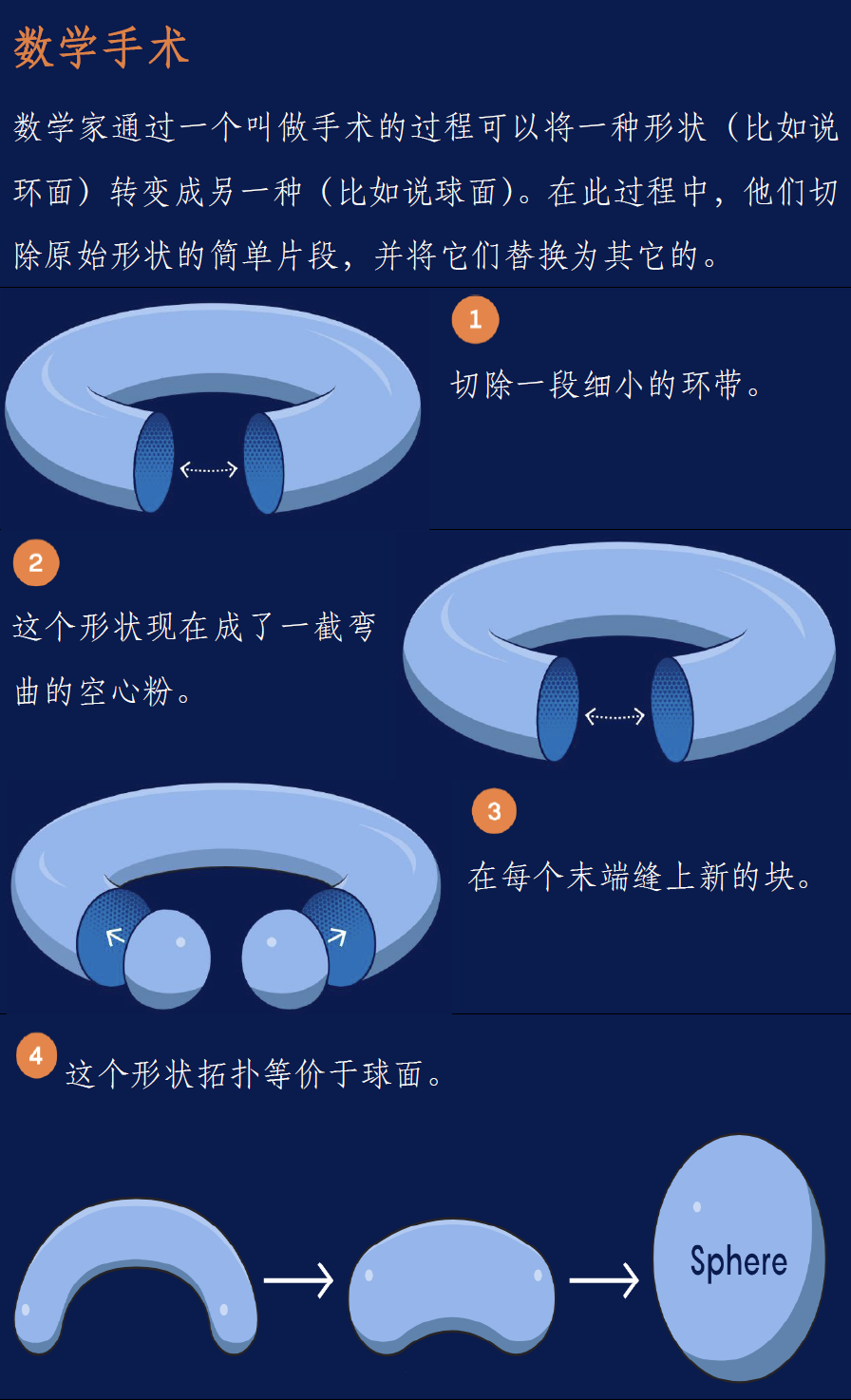
结果是一个常规球面——事实上，不存在2维奇异球面。但在某些维度里，手术会把一些流形转变成常规球面，而另一些转变成奇异球面。有时候甚至还存在另一种可能性：根本不可能转变成球面的流形。

要可视化最后一种情形，我们再次审视环面，不过这次我们给它一些特定的扭曲来阻碍手术：

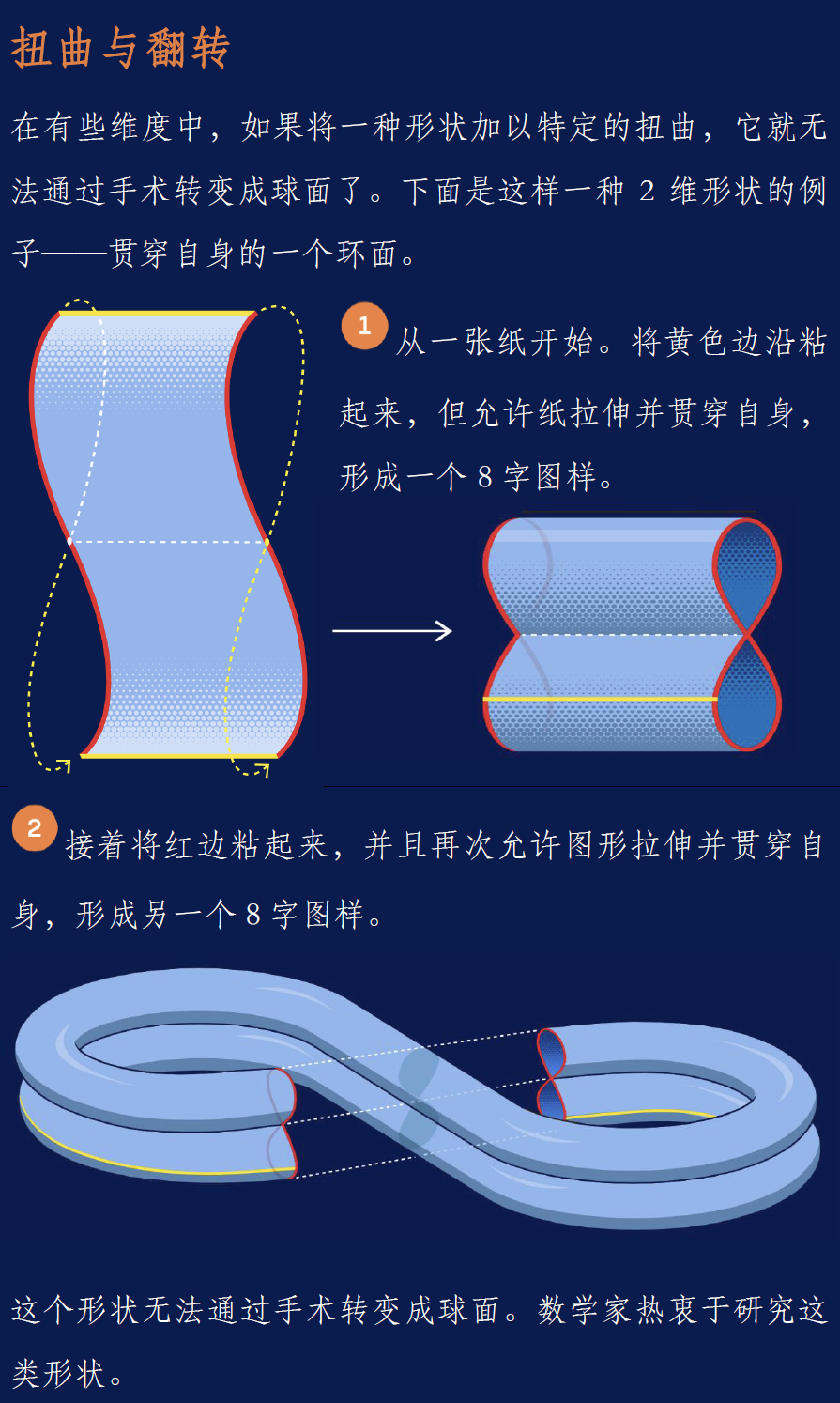
数学家证明，不存在任何手术可以将这一扭曲环面转变成球面，无论球面是常规的还是奇异的。这是一种截然不同的流形种类。

1960年，法国数学家Michel Kervaire提出了一个不变量——对于给定光滑流形你可以算出来的一个数——当流形可以通过手术转变成球面时这个数为0，而不可以时为1。因此普通环面的Kervaire不变量为0，而扭曲环面的Kervaire不变量则为1。

Kervaire使用他的不变量探索了不同维度中可能出现的流形的种类。他甚至还利用它提出了一种没有Kervarie不变量的10维流形，不管是0还是1——这也就意味着这一流形过于弯曲，没有任何合理的光滑性概念。

没人想象过这种流形可能存在。领略到这一全新不变量的威力之后，数学家们一拥而上，想确定不同维度中各种流形的Kervaire不变量。

在数年内，他们就证明出，Kervaire不变量为1的扭曲流形在维度2,6,14和30中存在。这些维度符合一种模式：每个数都比2的一个幂次小2（例如，30是2⁵-2）。1969年，数学家William Browder证明这种形式的维度是容纳Kervaire不变量为1的形状的仅有可能。

人们很自然地推测扭曲流形会存在于所有这种形式的维度里：62,126,254，以此类推。基于这一假定，有个数学家甚至构建了关于奇异球面和其它形状的一整套猜想。可是原始的这一假定仍然还存在出错的可能。这种可能性逐渐被人们称作末日猜想，因为它会颠覆所有这些其它猜想。

读研究生时，徐宙利被警告过不要试图解决Kervaire猜想。然而这一问题始终“源源不断地散发着魅力，”他说。

确实，尽管数学家们在1984年证明了扭曲流形在62维中存在，之后再没人能够证明这类流形在任何一个剩余维度中存在了。随着一个个搜索的穷尽，数学家们最终耗光了动力，而这一问题也成了死水一潭。

2009年，“为了遏止遗忘的趋势”，数学家Victor Snaith撰写了一本书，探讨了在Browder列表上所有维度都存在Kervaire不变量为1的流形的意义。不过，Snaith在前言中提醒，“这可能成为一本关于虚拟对象的书。”

如果Snaith的书晚出版一年，读起它来就完全不一样了。就在书出版的几周后，Hopkins与另两位研究者就让数学家们大吃了一惊。他们宣称Snaith对读者的提醒是再恰当不过了：末日猜想是对的。他们证明，Kervarie不变量为1的流形不可能存在于254及更高维度。

这一结果将数学家们置于一个神奇的处境。在所有维度的无数种可能形状里，仅仅只有一个维度中的形状还未能被分类。用罗彻斯特大学数学家，末日猜想证明的作者之一Douglas Ravenel的话来说就是，还有“一个巨大的悬念”。这个悬念就是126维。

存活至无穷

2011年，徐宙利作为研究生新生来到了芝加哥大学，计划研究流形的计算方面。他的导师Peter May建议他去研究126维问题，因为数学家认为它很可能涉及大量的计算。May把徐送到西北大学Mark Mahowald那里。Mahowald是Kervaire不变量问题的专家，甚至把他的帆船命名为其中一个关键符号——，也就是“Thetajay”。

不过Mahowald——他2013年去世——立即否决了这一建议。126维问题太难了，他告诉徐，——是一个“终生问题”。取而代之，他将这个年轻数学家引导到低维度下的相关问题上。

可是对于徐来说，126维问题始终“源源不断地散发着魅力”，他说。

王国祯研究复杂的对象，以获取对难以想象的高维形状的见解。

解决这一问题的潜在策略并不神秘。数学家们早就知道关于奇异球面和其它流形的关键奥秘蕴含在球面的所谓稳定同伦群这一对象中。这些是函数或者说“映射”的集体，它们会把高维球面中的点映到低维球面上去。

例如，想象这样一个映射，它把一个44维球面的每个点都映到一个33维球面的一个点上。这一映射本质上会把大球面的11维压缩掉。如果你在小球面上选定某个点，并找出大球面上映射到它的所有点，这些点通常会形成一个11维流形。

现在考虑你的小球面上所有不同的点。大体来说，每个点会给你一个不同的11维流形。因此你的映射不只是产生了一个11维流形。它产生了大量11维流形。

一个稳定同伦群就是一个集合，其中每个元素都是一组这样的映射。

数学家们知道要在一个给定维度下解决Kervaire不变量问题，他们只需要理解那个维度的稳定同伦群就行了。只是有一个难点：稳定同伦群的理解是拓扑学中最基础，也最具挑战性的问题之一。“我不指望在我孙女那一代就能解决它，”Ravenel说。

于是取而代之，数学家们逐步地逼近这一问题。自1958年以来，他们一直在把稳定同伦群结构的信息整理成由被称为Adams谱序列的点构成的图册。这本图册浩瀚无比，但尚未完成。

林伟南写了一个计算机程序来帮助他和同行解决关于高维形状奇特性质的一个数十年之久的猜想。

想象一本有无穷页面的书，每一页由无穷列的点组成。我们翻开书，检查单独的一页。这一页的每一列都代表着一个维度。给定列的每个点代表着那个维度下球面映射的不同可能的“口味”。总是只有两种口味，“常规的”或是“超脆的”（或者说，Kervaire不变量为0或1的）。

在某些方面，这本书出奇地重复——每一页都有一系列相同的列，并且每一列有许多相同的点。但当你翻过这些页面时，你会注意到一个关键的不同之处：每一页递进地刻画了球面映射与流形的更精细的内容。图册的早期页面仅仅是真相的近似。随着你往后翻，这些近似越来越好，等到了图册的末页——也被称为“无穷”页——表示变得完美。

浏览这一图册就像是在用愈加强力的望远镜来探索流形的宇宙。在第一页，每个流形的细节都是朦胧的，并且许多并不真正归属其中的流形被错误地纳入进来了。可是当你使用一台更好的望远镜，你就能探测出一个流形有着某种“瑕疵”，可以将它从图册中排除出去。在此情形下，你会把相应的点从图册所有后续的页面中都删除掉。如果你的望远镜没能发现任何瑕疵，那么点会存活到下一页，在那里你希望用一台更加强大的望远镜去观察它。

1969年，Browder证明图册的126列的一个特殊点是该维度下Kervaire不变量问题的关键所在。如果这个点存活到无穷页，那么大量的126维流形一定会以两种口味出现：其中一半的Kervaire不变量为0，而另一半则为1。如果那个点没能存活，那么126维流形将只有一种味道，Kervaire不变量为0。

对于126列的那个特殊点，存在105种不同的假定方式让它在无穷页之前就可能消失。要一一处理这些可能性，徐跟他的长期合作者兼前大学室友王国祯搭起了档。当他们发展出新的计算技术后，就传给徐从研究生时代就认识的数学家林伟南。林编了一个程序，得以排除掉101种可能性。接着，又花了一年时间，这些研究者艰难地发展出新的方法将剩下四种可能性也排除掉了。他们得出结论，Browder的特殊点确实存活到了无穷页——这就意味着126维存在Kervaire不变量为1的流形。

在团队宣布结果之前，数学家认为这个计算过程根本没法完成，Hopkins说。这一新工作是一项“计算壮举”，他补充道。其中的方法可能最终会帮助数学家们绘制巨型图册的更多部分。

尽管新文章证明了126维存在奇特的扭曲形状，它并没有给出构造它们的思路。研究者们已经在前面四个特定Kervaire维度2,6,14和30中都找到了特殊的扭曲形状。不过还没人在62或126维中找到一个，哪怕在这些形状存在的任意一个维度里，它们都占据了所有可能形状中的整整一半。尽管它们如此繁多，“我们却没法真正找到一个，”Tillmann说道。

如果数学家知晓了如何在62和126维中构造扭曲形状，这将对这六个维度为何如此特殊——为何仅仅在这些维度中可以构建这类扭曲形状——给出一些提示。“通常当【类似】这种情况出现时，会存在某种非常优美的构造。”Hopkins说，“它转瞬即逝，因为它必须只运作五到六次，而非无穷多次。”新工作“进一步鼓舞着人们去真正发现这六种对象的特定构造方式。”

而Kervaire问题仅仅是蕴含在Adams谱序列中的维度怪异性类别之一。特定的Kervaire维度对应着图册第二行中的六个特定点。最近，徐和哥本哈根大学的Robert Burklund发现在图册的第三行也有一些特定维度似乎呈现出另一种古怪行为。还没有人知晓何种奇异流形对应于这些维度中的特定点——但数学家们渴望去发现。

后续行的发现很可能也会到来，徐称，“以后一定还会有层出不穷的故事，等待着我们去探索。”

原文链接：

https://www.quantamagazine.org/dimension-126-contains-strangely-twisted-shapes-mathematicians-prove-20250505/

转载本文请联系原作者获取授权，同时请注明本文来自左芬科学网博客。

链接地址：https://wap.sciencenet.cn/blog-863936-1486993.html?mobile=1

收藏

分享