 精选
精选
全新证明揭晓连通网络数十年赌约的胜负
据数学传言称,1980年代晚期Peter Sarnak与Noga Alon就最优图订立了一个赌约。现在他们被证明都错了。
Leila Sloman 撰
左 芬 译
【译者按:原文2025年4月18日刊载于Quanta Magazine,链接见文末。】
这起源于一个赌约。
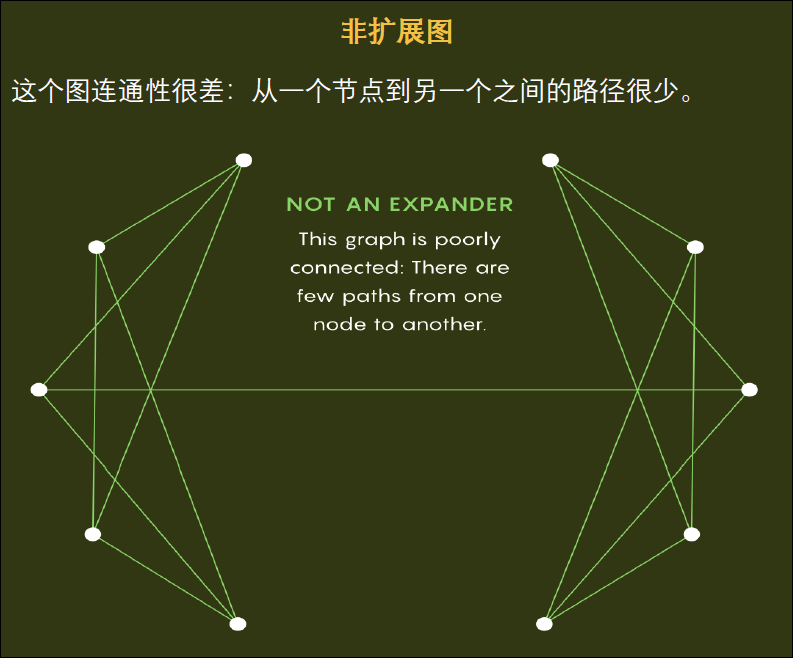
1980年代晚期,在洛桑市的一次会议上,数学家Noga Alon和Peter Sarnak进行了一场友好的争论。俩人都在研究大量节点和边组成的对象,也就是所谓图。特别地,他们想要更好地理解一种反常的图,所谓扩展图。它们拥有相对较少的边,但仍然是高度互连的。
争论的是最佳的扩展图:那些尽其可能连通的。Sarnak主张这种图是稀有的;他和两个合作者随后立刻发表了一篇文章,使用数论中的复杂想法来构建实例,并且声称任何其它构造也会同样难以获得。而Alon这一方则仰仗随机图往往展示出各种最优性质这一事实。他认为这些极佳的扩展图会是常见的——以致当你从大量备选中随机选择一个图时,你几乎可以确保它就是一个最优扩展图。
如今,Alon和Sarnak是普林斯顿大学的同事。赌约的细节经过这中间的35年已经变得模糊。“这并不是个非常认真的赌约,”Alon回忆道,“我们甚至没有约定好赌注是什么。”
但传言仍在继续,鼓舞着数学家们去找出答案。去年12月,利用物理学中的一个关键现象——并将其推进到极限——三位数学家最终做出裁定。Alon和Sarnak都错了。
扩展的极限
数学家们自从1960年代开始研究扩展图以来,已经把它们用于建模大脑,开展统计分析,以及构建纠错码——对信息进行加密,使得它们即使在传输过程中被篡改了也还能阅读。因为扩展图的边很少,它们极其高效。但又因为它们高度连通,它们依然能抵御潜在的网络错误。这一冲突,Sarnak称,“使得它们既违背直觉,又非常有用。”
因此数学家想要更好地理解它们。减少边数和增加图连通性之间的这一冲突能推进到何种程度?达到最大冲突的极佳扩展图又有多普遍呢?
要回答这些问题,研究者们需要精确地定义扩展。有许多方法做到这一点。一种是,要把扩展图分成两个分离的片段,你得删除许多边。另一种是,如果你沿着图的边漫游,每一步随机选择你的方向,那么用不了多久你就可以遍历整个图。

1984年,数学家Józef Dodziuk证明所有这些扩展的测度都通过一个量关联起来——至少,对于某种类型的图来说。在这些所谓正则图上,每个节点都有着相同数目的邻边。这确保了整个图的边数相对较少。接下来,要让它成为扩展图,你得证明它的连通性很好。这正是Dodziuk的量介入的地方。
要计算这个量,你必须先构造一个由0和1组成的数组,称为邻接矩阵。这一邻接矩阵代表着你的图里哪些节点之间有边连接着,哪些没有。
接下来你可以用这个矩阵计算一串数,所谓本征值,它们提供了关于原始图的有用信息。比如,最大的本征值给出了图中每个节点连着的边数。Dodziuk发现次大的本征值告诉你图的连通情况。这个数越小,图的连通性就越好——也就成了更好的扩展图。
在Dodziuk的发现之后不久,Alon和Ravi Boppana就证明,如果正则图的每个节点有条边,那么第二本征值不可能会比
还小多少。如果一个正则图的第二本征值接近这一“Alon-Boppana下界”,就是一个好的扩展图;相比于其它拥有相同边数的正则图而言,它的连通性更好。而如果一个正则图的第二本征值真正达到这一下界的话,这个图就是能够实现的最佳扩展图。
1980年代晚期,数学家Peter Sarnak(左图)和Noga Alon就一种最优图的普遍性订立了一个赌约。结果两人都错了。
对于某些数学家而言——其中包括Sarnak——Alon-Boppana下界是一个迷人的挑战。他们好奇,是否能构造出达到这一极限的图来呢?
押注随机性
在1988年发表的一篇里程碑式的文章中,Sarnak, Alexander Lubptzky与Ralph Phillips找出了方法。利用印度数学奇才Srinivasa Ramanujan的一个高度技术性的数论结果,Sarnak和他的合作者们生成了达到Alon-Boppana下界的正则图。正因如此,他们把这些最优扩展图称为“Ramanujan图”。(就在同一年,Grigorii Margulis使用不同但同样高度技术性的方法构建出了其它实例。)
“直觉上,似乎你可以预料到”在构建Ramanujan图时会遇到这种几乎令人望而却步的困难性,普林斯顿高等研究院的Ramon van Handel说道,“看上去最佳的可行图应该非常难以获得。”
可是在数学里,难以构建的对象事实上往往出奇地常见。“在这种事情上这是一个普遍现象,”van Handel说道,“你能构想的任何实例都不会有这些性质,但一个随机的例子却会。”
在花了十年多时间研究与随机图相关的矩阵后,姚鸿泽解决了有关它们行为的一个重要问题。
有一些研究者,包括Alon在内,相信同样的情况也会出现在Ramanujan图上。Alon觉得,发现这些图所需的艰辛更体现的是人脑的不足,而非这类图的匮乏。这一信念引发了Alon与Sarnak的赌约:Sarnak押注如果你汇集所有正则图,极少的份额会是Ramanujan的;Alon则认定几乎所有的都会是。很快,Alon与Sarnak赌约的流言就在数学界传开了,尽管对现场的记忆有所差别。
“跟你说实话,这更多的是传言,”Sarnak承认,“其实我都不记得这桩事了。”
数十年后,2008年一份对大量正则图以及它们本征值的分析表明答案并非泾渭分明的。有些图是Ramanujan的,有些则不是。这只会让找出准确的份额更加艰辛。要证明一种性质适用于所有图(或者一个图也不适用),数学家们有大量的工具可以借助。但要证明一些图是Ramanujan的,而其它不是——这需要精度,可图论家们完全不清楚这一精度从何而来。
最终,来自完全不同的一个数学领域的一位名叫姚鸿泽的研究者解决了这一问题。
“疯狂”构想
当图论家们还在把握2008年那项研究的推论时,哈佛大学教授姚鸿泽已经痴迷于本征值好些年头了。这些本征值出于一类广泛得多的矩阵,它们的元素是随机生成的——比如,通过抛硬币或者执行其它一些随机过程。姚想弄清矩阵本征值会如何随着你所采用的随机过程而变化。
这一问题起源于1955年,当时物理学家Eugene Wigner使用随机矩阵来建模像铀这样的重原子核的行为。通过研究这些矩阵的本征值,他希望对这一体系所拥有能量的多少获取见解。Wigner很快注意到一些奇怪之处:不同随机矩阵模型的本征值似乎全都展现相同的模式。对于任何随机矩阵,每个本征值也是随机的;选定一个取值区间,它就会有一定几率落在那个区间内。但随机矩阵的元素到底是只取1和-1,还是可以取任意实数,看起来无关紧要。在不同情形下,本征值落到某个取值区间的几率并不改变。
物理学家Eugene Wigner在他研究的各种随机体系中观察到惊人的普适行为。数学家们如今拓展了该行为的适用范围。
Wigner猜想,任何随机矩阵的本征值都会满足相同的概率分布。他的预言随后被称为“普适性猜想”。
这一想法很“疯狂”,姚说道,“许多人不相信他所说的。”但随着时间的推移,他和其他数学家证明了普适性猜想对许多种随机矩阵都成立。一次又一次地,Wigner被证实。
姚如今想要看看他能把这一猜想推进到多远。“我试图寻找有点超出我们对标准矩阵的认知的一些问题。”他说。
于是在2013年,当Sarnak建议姚研究跟随机正则图相关的矩阵的本征值时,他接受了这一挑战。
如果姚能够证明这些本征值也满足普适性猜想,他就会知道它们的概率分布。接着他可以用这一信息计算出第二本征值达到Alon-Boppana下界的可能性。换句话说,他就能对Sarnak和Alon赌约中Ramanujan图在正则图中的比例给出确切的答案。
“[Sarnak]一直在奚落我,‘你能做到吗?’”姚说。
于是他出发了。
近乎终点
许多种随机矩阵,包括启发Wigner猜想的那些,都拥有良好的性质,可以用来直接计算它们本征值的分布。但邻接矩阵并不具有这些性质。
大约在2015年,姚和他的研究生黄骄阳以及另外两个合作者想出了一个计划。首先,他们使用一种随机过程来对他们的邻接矩阵里的元素进行微调,得到一个全新的随机矩阵,而它会展现所需的性质。他们接着计算新矩阵的本征值分布,证明它满足普适性猜想。最后,他们证明所使用的微调过于微小而不足以影响原始矩阵的本征值——从而表明原始矩阵也满足普适性猜想。
黄骄阳在概率论中的研究引导着他去探索数学、物理和计算机科学中的问题。
2020年,在黄博士毕业之后,这几位数学家得以使用这一方法将普适性猜想推广到一定规模的正则图上。只要一个图有足够多的边,它的第二本征值就会具有Wigner数十年前研究过的同一分布。但要得出Alon与Sarnak赌约的结果,他们还需要证明普适性猜想对所有正则图适用,而不仅仅是一部分。
接着,2022年秋天,一个名叫Theo McKenzie的博士后研究员来到了哈佛,急于学到更多黄、姚及其合作者在他们2020年证明中所发展的工具。这有大量进度需要赶上。“我们毕竟已经研究了这么长一段时间,”姚说。
但McKenzie“毫不畏惧”,加州大学伯克利分校数学家,McKenie之前的博士导师Nikhil Srivastava说道,“他勇于直面这种极其困难的问题。”
在研究了黄和姚的方法数个月后,McKenzie终于觉得准备好了,可以为团队提供新鲜血液了。“你需要人来检查许多细节,提出许多不同的问题,”姚说,“有时候你需要更多人力。”
最初,这三个数学家只能满足于一个部分结果。他们无法执行证明策略的第二步——计算微调过的矩阵的本征值分布——到足够精确的程度,以证明所有正则图的普适性猜想。但他们能证明本征值仍然满足一些重要性质。这些性质强烈地表明猜想会是对的。
Theo McKenzie是最后加入到这个数学家小组的。他们解决了关于所谓Ramanujan图的本质的一场历时数十年的争论。
“我知道他们已经到了彻底解决这一问题的临界线了,”Sarnak说。
结果,在一个独立的项目中,黄已经在把玩他们所需的最终要素了。
封顶
黄已经在独立地研究一套方程,所谓圈方程。它们刻画了一个随机矩阵模型中本征值的行为。他意识到,如果他、McKenzie和姚能够证明他们的矩阵以很高水平的精度满足这些方程的话,这就能为他们提供实施第二步所需的缺失信息。
这就是他们所做的。在数个月的艰辛计算后,他们得到了证明。所有的正则图都满足Wigner的普适性猜想:随机选择一个正则图,它的本征值都会展示同样的已知分布。
这也意味着仨人组如今知晓了第二本征值取值的精确分布。他们可以计算出达到Alon-Boppana下界的那些本征值的份额——也就是,随机正则图的多大份额会是完美扩展图。在三十多年过后,Sarnak和Alon终于知晓了他们赌约的答案。这一份额事实上大约是69%,使得这种图既不常见,也不稀少。
Sarnak最先得到这一消息。“他告诉我们,这是他有史以来得到的最好的圣诞礼物,”黄说道,“所以我们觉得这一切都是值得的。”
这一结果也表明普适性猜想比研究者们预想的更加普遍,更加强大。数学家们希望在这些界限上继续推进,并且利用新证明的技术来应对相关的问题。
不过与此同时,他们也为在Ramanujan图的神秘领地里又前进了一步而沉浸在喜悦中。
“我俩都算是错了,”Alon说。“不过,”他笑着补充道,“我要稍微对那么一点点,因为概率大于一半。”
原文链接:
https://www.quantamagazine.org/new-proof-settles-decades-old-bet-about-connected-networks-20250418/
转载本文请联系原作者获取授权,同时请注明本文来自左芬科学网博客。
链接地址:https://wap.sciencenet.cn/blog-863936-1485149.html?mobile=1
收藏

