博文
存在与否?两难的设计问题终获解决
||
存在与否?两难的设计问题终获解决
关于人群分组的150年难题最终被解决,但许多谜团仍遗留。
Erica Klarreich 著
左 芬 译
【译注:原文2015年6月9日刊载于QuantaMagazine。】

由The Graphics Fairy和Old Design Shop提供的拼贴画,
“三个女生”。
1850年,兰开夏郡克罗夫特和索斯沃思教区的Thomas Kirkman教士在一份娱乐性数学杂志《绅士小姐日记》上提出了一个看似平平无奇的谜题:
“学校里的十五位年轻女士在连续七天里三三并肩出行:要求每天对她们进行安排,使得没有两人并肩两次。”(所谓“并肩”,Kirkman指的是“在一个群里”,因此姑娘们是三人成群出行的,并且每对姑娘应该恰好有一次出现在同一个群里。)

Thomas Kirkman的通俗数学谜题最初出现在1850年那一期的《绅士小姐日记》。
拿出铅笔和纸试一下,你很快就会发现这一问题比看上去的要难多了:在给女生们排好前两三天后,你几乎不可避免地会让自己陷入困境,又不得不从头开始。
这一谜题以其简洁性吊足了读者们的胃口,并且在发表后的岁月里缓慢地,近乎维多利亚式地疯狂传播开来。它收获了业余爱好者们的种种解答,杰出数学家们的多篇论文,甚至被“一位女士”写成了一首诗。诗是这样开头的:
有位老师声名好,
十五女士齐来到。
并肩出行把城绕,
河边草地绿已早。
尽管Kirkman后来抱怨他重要的数学贡献都被这个智力游戏的风头给盖过了,可当另一位著名的数学家James Joseph Sylvester声称早就提出了这一问题并使得“它进而如此家喻户晓,让无数敏感的心颤动”时,他又迅速地捍卫了自己的领地。
九女生出行问题:
求解Thomas Kirkman谜题的变种,将九女生安排成小群体出行。快点想——要计时的。【译注:答案见文末。】
这个谜题可能看起来只是个有趣的游戏(一个简化版如上图),但它的发表却帮助建立了组合设计论这样一个数学领域,而这一理论如今已经写进了数不胜数的指南书里。最初只是关于如何将人群分成组别——即所谓“设计”——的一类难题,而后续却在试验安排、纠错码、加密、锦标赛对阵甚至彩票方面都得到了应用。
然而在Kirkman传播他的女生问题超过150年后,这一领域内最基本的问题仍未得到解答:这样的谜题总是有解吗?Kirkman的谜题代表着一类更广泛问题:如果你有n个女生,你是否能生成大小为k的一些群体,使得每个小一些的,大小为t的集合在恰好一个大群体里出现?这样一种安排被称为一个(n,k,t)设计。(Kirkman的设置里还存在额外的难点,这些群体必须能按“天”整合。)
不难看出,并非所有n,k和t的选择都可行。举例来说,假定你有六个女生,你就没法找到女生三人组的集合,使得每对女生恰好出现一次:每个包含“Annabel”的三人组会包括涉及她的两个对次,但Annabel出现在五个对次里,而五没法被二整除。许多n,k和t的组合会被这类整除性障碍立刻排除。
对于那些没法排除的参数,也并没有捷径可以找出设计来。在很多情况下,数学家通过蛮力和代数方法的结合找到了设计。但设计理论家们也发现,有些参数的实例,比如 (43,7,2),尽管所有的可除性要求都达到了,却并不存在相应的设计。数学家们纳闷,这些情形到底是例外,还是普遍的?“这是组合学中最著名的问题之一,”耶路撒冷市希伯来大学的数学家Gil Kalai说道。他回想起曾在一年半前就这个问题和一个同行打赌,而最终得出的结论是“我们永远无法知晓答案,因为它实在太难了。”
然而就在两周后,牛津大学一名叫Peter Keevash的年轻数学家证实Kalai是错了。2014年1月,Keevash证明,如果可除性要求满足的话,设计一定存在,除了少量例外。在今年4月发布于科学预印本网站arxiv.org的第二篇论文中,Keevash说明了对给定参数如何计算设计的近似数目。这一数目指数式地增长——例如,将19个女生分成三人组使得每对女生只出现一次就有超过110亿种方式。
这一结果“在设计理论范围内有点翻天覆地的感觉”,剑桥大学数学家Timothy Gower说道。将设计理论与概率论结合起来的证明方法也是所料未及的,他说,“Keevash的工作惊世骇俗。”
大捞一笔
在设计理论的早期数学家就意识到这一领域与代数和几何的某些分支紧密关联。例如,被称为“有限射影平面”的几何结构——类似于透视画法中用到的点和线的集合——其实就是设计的伪装。最小的这种几何,由七个点的集体构成的所谓Fano平面,给出一种(7,3,2)设计:每条线恰好包含3个点,而每对点也恰好出现在一条线上。这种联系为数学家提供了一种生成特定设计的几何方法。
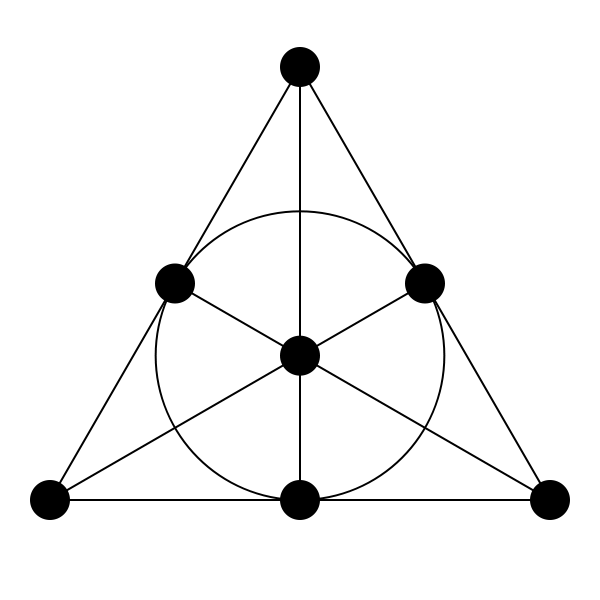
被称为“Fano平面”的几何结构对应着一个(7,3,2)设计。
1920年代,著名统计学家Ronald Fisher描述了如何利用设计来规划农业试验,使得多种作物可以在不同试验条件下进行对比。而如今,坦佩市亚利桑那州立大学的计算机科学家Charles Colbourn称,“【种植试验软件】的主要任务之一就是构造设计。”
从1930年代开始【译注:考虑到纠错码1948年才诞生,作者这里想说的应该是1950年代。】,设计也被广泛用于构造纠错码,也就是在含噪声的信道中也能精确传送信息的体系。设计可以巧妙地转换成纠错码,因为它们生成的集合(女生群)彼此相差很大——例如,在原始的女生问题中,没有哪两个女生三人组包含一个以上相同女生。如果你使用女生群作为“码字”,那么当发送某个码字出现一个传输错误时,你仍能弄清发送的是哪个,因为只有一个码字会与错乱的信息相近。早期最著名的纠错码之一,Hamming码,本质上就等价于(7,3,2) Fano平面设计,而另一种与设计相关的纠错码【译注:扩展Golay码。】在1970年代早期被用于编码水手9号飞船发送回地球的火星照片。“有些极其优美的编码正是基于设计构造出来的,”Colbourn说道。
2005年到2011年间,设计理论甚至可能还曾被赌徒们利用,从马萨诸塞州制定不完善的Cash WinFall彩票中套取数百万美元。这一彩票要求从46个数字中选出6个;6个全对则赢得奖池,而对5个可以赢得小一些的奖金。
从46个数字中选出6个有超过九百万种可能的方式,使得购买所有可能组合的彩票的花费远远超过了游戏的典型奖池。然而,一些团伙意识到,购买数十万张彩票可以让他们靠赢取大量小额奖金而获得盈利。在这种策略下最好的彩票搭配可以说就是一个(46,6,5)设计,因为这样产生的6数字彩票可以使得每个5数字组刚好出现一次,从而确保赢得奖池或者所有5数字奖金。
至今还没有谁找到过一个(46,6,5)设计,Colbourn称,但存在与之足够接近的设计可以加以使用。有没有赌徒利用这样的设计“从该彩票中毫无风险地汲取财富呢?”麦迪逊市威斯康辛大学的数学家Jordan Ellenberg在他的书《魔鬼数学》中讨论Cash WinFall彩票时写道。Ellenberg接着说,如果他们没有,那倒是有点可惜了。
要列出设计的所有应用太难了,Colborun表示,因为新的在不断被发现。“我一直为设计在如此多完全不同的地方出现而感到惊讶,尤其是当你完全没预料到的时候。”他说。
完美设计
由于设计的应用数目激增,数学家在参考书里塞满了设计列表,以便哪天会派上用场。作为1016页的《组合设计手册》的联合编辑,Colbourn说道,“我们列了表格来说明,‘对于这套参数,已知有300000种设计。’”
尽管实例繁多,数学家们始终没能弄明白在哪些情形下设计必然会存在。他们唯一彻底理解的情形是最小参数t等于2的时候:帕萨迪纳市加州理工学院的Richard Wilson在1970年代中期证明,当t=2时,对于任意k至多有有限数目的例外——n的取值满足可除性规则但设计不存在。
但是当t大于2时,没人知道设计是否会普遍存在——而对于大于5的t值,他们甚至没法找出一个设计的实例来。“有些人坚信【设计】必然存在,但其他人则坚信这过于苛求了,”Colbourn说道。
1985年,亚特兰大市埃默里大学的Vojtěch Rödl给数学家们提供了一个安慰奖:他证明几乎总是有办法获得一个好的近似设计——其中可能只有少量份额的所需集合缺失了,但不会很多。Rödl采用了一种随机过程来逐渐地累积起大量集合——这一过程后来被称为Rödl蚕食,因为正如Keevash所说的,“不是试图一次全都吞下,而是小口地咬。”
自那以后,Rödl蚕食成为了组合学中广泛应用的工具,甚至还被用到了数论当中。比如说,去年,数学家们就利用它确立了相邻素数的间距能到多远。【译注:2023年年底,人们利用Rödl蚕食改进了高维空间中球堆积的渐近下界。】
不过数学家们也认同蚕食法对于构造完美设计不是很有用。毕竟,在Rödl过程的最后,你通常会缺失所需小集合的少量份额。为了得到完美设计,你得加入一些额外的大群体来覆盖这些缺失集合。但是除非你格外幸运,这些新的群体会与设计里已有的一些群体存在重合,从而产生席卷整个体系的新错误。
设计看上去就是不具有这种弹性,可以容许一种随机方法的运作。看起来“完全不可能”,Gower说道,“类似Rödl的方法可以用来得到完美设计。”

牛津大学的Peter Keevash。
然而,去年——Rödl 的工作过去近三十年后——Keevash 表明,一种兼具弹性和刚性的方法可以用来控制错误的倾泻。Keevash 修改了 Rödl 的构造,让蚕食过程从女生群的一个特定集体,也就是所谓的“模板”出发,而模板具有极其良好的代数性质。在蚕食的最后,仍会有错误需要纠正,但 Keevash 证明一旦这些错误传播进模板,它们总可以通过有限步在那里纠正过来,从而生成一个完美设计。“整个证明极其精巧,是一项难得一见的成就。”荷兰拉德堡大学的 Ross Kang 这样评价。
“我觉得好几年前,没人会想到证明就将浮出水面了。”Cobourn说道,“这是一个异乎寻常的突破。”
对于纯粹数学家来说,Keevash的结果在某种意义上意味着故事的终结:它表明,对于任何参数t与k,所有满足可除性条件的n的取值都能给出设计,除了至多有限数目的例外。“它在某种意义上扼杀了一整类问题,”Gowers说道。
但Keevash的结果仍然为那些关注实用设计的人们留下了许多未解之谜。理论上,他的模板-蚕食方法可以用来构造设计,但目前来说仍不清楚n得多大他的方法才会奏效,也不清楚他的方法生成的算法要运行多久。而且尽管Keevash证明了设计几乎总是存在,但对于你可能关注的特定参数组合,他的结果并没有表明是否有设计存在。“对此人们大概还得一代代地研究下去,”Wilson称。
不过,Keevash的结果仍将转变试图发现设计的数学家们的思维模式,Colbourn说道。“之前,人们不清楚是该把重心放在构建设计还是证明其不存在上,”他说,“而现在,至少我们知道应该集中精力去构造它们。”
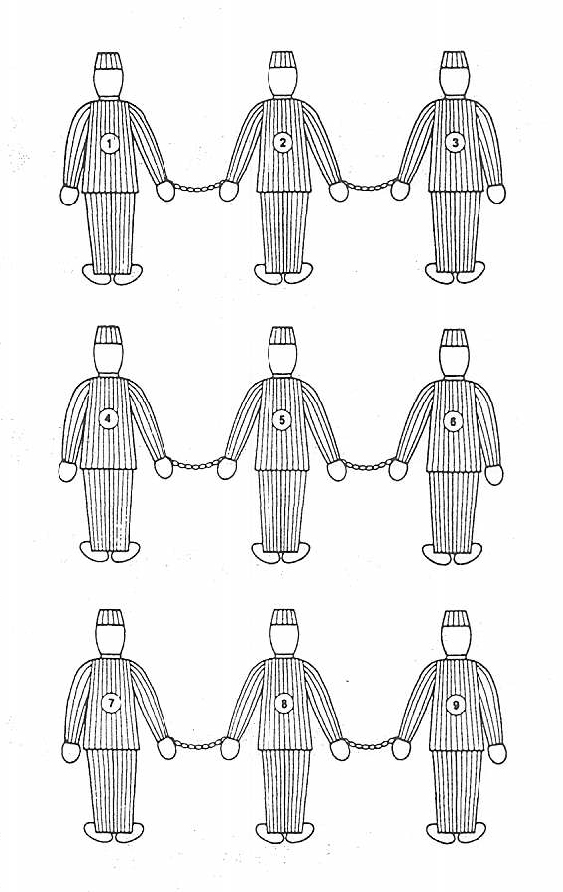
Martin Garder的书《最后的消遣》中的九囚徒问题插图。
而特定设计上的信息短缺则给趣味数学家们留下了大量好玩的谜题。因此本着Kirkman的精神,我们也为尊敬的读者留下一道智力题,由英国解谜爱好者Henry Ernest Dudeney于1917年构思,后由Martin Gardner推广的女生谜题变形版:在六个工作日的每一天(在Dudebey的未启蒙时代,周六仍然是工作日。),把九个囚徒带到室外三个一排地进行操练,每一对相邻的囚徒用一副手铐锁起来。能否在整个六天里对囚徒进行排列,使得每对囚徒只被锁在一起刚好一次?
Dudeney这样描述他的谜题:“与十五女生的旧问题截然不同,它会是一个引人入胜的游戏,为在业余时间寻找答案的人们带来巨大的乐趣。”求解快乐!
附录:九女生出行问题的答案见下图
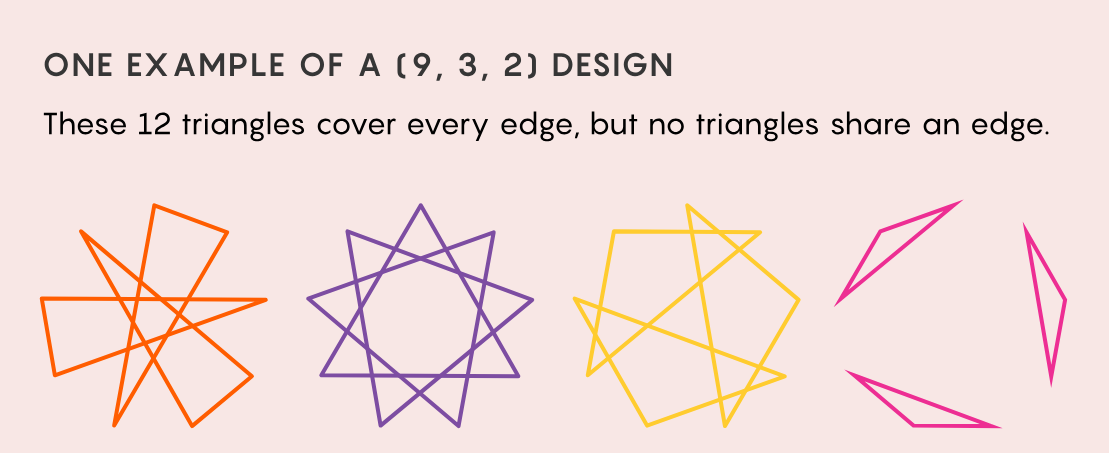
https://wap.sciencenet.cn/blog-863936-1457066.html
上一篇:研究者挫败随机性并创建理想编码
下一篇:在高度连接的网络里,圈一定存在