 精选
精选

进步的多重解释:范式转换、模型依赖现实与复杂性视角——以流体力学的演进为例
叶菲楠 李侠
1.上海交通大学 科学史与科学文化研究院,上海 200240
摘要:流体力学的发展经历了多个关键阶段,从经典流体理论的建立到现代数值模拟技术的应用。库恩的范式转换理论、霍金的模型依赖现实观以及复杂科学的基本概念提供了全新的视角,帮助解释流体力学的演进。库恩的范式理论指出,科学进步不仅依赖知识的积累,更是通过对既有理论框架的革命性转换而实现。在流体力学的发展中,从牛顿流体理论到纳维–斯托克斯方程,再到现代湍流模型的不断演化,都一定程度上体现了对原有范式的修正与扩展,从而可以被视为库恩所描述的‘范式转换’进程。霍金的模型依赖现实观则强调科学模型并非客观现实的直接反映,而是根据观察对象和研究需求选择的工具,流体力学中的多样性模型正是这一观点的体现。复杂系统理论进一步揭示了流体力学中湍流等现象的非线性、多尺度与自组织特性,这为模型优化和精确模拟提供了新思路。结合这些理论,流体力学的演进不仅展示了范式与模型选择的互动,还揭示了科学进步的非线性特征,为工程科学提供了新的理论支持。流体力学的发展体现了科学理论和应用的动态交替,加深我们对科学理论变革机制和工程哲学的理解,也为未来科技政策的制定以及科技管理水平的提高提供了有益的视角。
关键词:流体力学;范式转换;模型依赖现实;复杂系统;工程科学
中图分类号:B15 文献标识码:A
引言
流体力学不仅是工程学科中的基础学科,更是推动现代技术创新和解决全球性挑战(如能源、气候变化、环境污染等)的关键领域。流体力学研究流体(液体和气体)运动规律及其与固体物体相互作用。[1]本文选择流体力学作为研究对象,除了其在工程科学中的广泛应用外,还在于流体流动的复杂性和多样性使其成为研究工程系统动态行为的重要模型。[2]
通过对流体力学发展历史的梳理,利用库恩(Thomas Kuhn)的范式转换理论(Paradigm shift theory)、霍金(Stephen Hawking)的模型依赖现实观(Model dependent realism)和复杂科学(Complex science)的视角,尝试分析哪种解释模式能更好地揭示流体力学理论进步的内在机制。这些理论模型的结合提供了更全面的解释框架,揭示了流体力学中的科学变革、模型选择及复杂现象的多样性和适应性。在流体力学中,从牛顿流体理论到湍流模型的演进,以及从经典的雷诺平均模型到大涡模拟(LES)和直接数值模拟(DNS)的发展,都体现了研究共同体对核心假设与方法的重大修正与拓展。[3]霍金的模型依赖现实观揭示出,模型的多样性和适应性推动了流体力学从经典理论向更复杂模型的转变。[4]复杂科学理论强调系统的非线性、涌现和自组织特性,揭示了湍流等复杂现象中的多尺度和多变量相互作用。这些理论的结合使我们能够更好地理解流体力学从经典理论到现代形态的演化过程,体现了科学发展的非线性和多样性,同时也为应对工程应用中的复杂流动问题提供了新的理论基础。
1 流体力学的历史演进概述
流体力学作为研究流体运动及其与周围环境相互作用的科学,其历史演进展示了科学理论与技术应用的不断深化与扩展。[5]问题的缘起可以追溯到古希腊时期,当时的哲学家和科学家通过观察和思辨,初步探讨了流体的基本性质和运动规律。亚里士多德(Aristotle)在其著作《动力学》中提出了流体静力学的基本概念,尽管其中存在诸如流体在运动时密度变化等错误观念,但他对流体状态的分类和基本运动规律的探讨为后世奠定了基础。[6]进入文艺复兴时期,科学方法的发展推动了流体力学的进步。伽利略·伽利莱(Galileo Galilei)通过实验研究探讨了流体流动的基本规律,特别是重力与流速之间的关系,他的实验方法强调了观察与实验在科学研究中的重要性,为流体力学的发展引入了实证主义的研究方法。[7]17世纪,艾萨克·牛顿(Isaac Newton)在其著作《自然哲学的数学原理》中系统地阐述了流体动力学的基本原理,提出了粘性理论,解释了流体内部摩擦力的存在,并引入了牛顿粘性定律,为经典流体力学奠定了坚实的理论基础。[8]18世纪末至19世纪,随着数学工具的完善和实验技术的进步,流体力学得到了迅速的发展。丹尼尔·伯努利(Daniel Bernoulli)在其著作《流体动力学》中提出了伯努利方程,描述了流体沿流线的能量转换。[9]19世纪中叶,乔治·加布里埃尔·斯托克斯(George Gabriel Stokes)和克里斯蒂安·路易·约瑟夫·欧拉(Christian Ludwig Joseph Euler)分别独立发展了流体动力学的数学描述,提出了斯托克斯方程和欧拉方程,这些方程描述了粘性和非粘性流体的运动,是现代流体力学的基石。[10]亨利·纳维(Claude-Louis Navier)和乔治·斯托克斯在19世纪中叶共同发展了纳维-斯托克斯方程,系统地描述了粘性流体的运动,成为现代流体力学的核心方程之一。[11]在19世纪末和20世纪初,随着工业革命的推进,对高效流体动力系统的需求不断增加,推动了流体力学理论与工程应用的深度结合。
进入20世纪后,流体力学迎来了现代进展的黄金时代,尤其是在计算技术和实验方法的革新推动下,流体力学研究取得了突破性的进展。计算流体力学的发展使得复杂流动问题的数值模拟成为可能,极大地扩展了流体力学的应用范围。随着计算机性能的提升和算法的优化,CFD能够模拟更高精度和更复杂的流动现象,如湍流、多相流和非牛顿流体的行为。[12]湍流理论从经典线性理论向统计力学和混沌理论的转变,提供了新的视角来理解和预测复杂流动的行为。非线性动力学和复杂系统理论的引入,使得科学家能够更好地描述和控制流体中的涌现现象和自组织(Self-organization)行为。同时,实验技术的进步,如激光多普勒测速(Laser Doppler Anemometry, LDA)和粒子图像测速(Particle Image Velocimetry, PIV),提供了更加精确和详细的流场测量手段,促进了流体力学理论与实际应用的紧密结合。[13]近年来,机器学习和数据驱动方法在流体力学中的应用,进一步推动了模型的优化和创新,使得流体力学能够应对更加多样化和复杂的工程挑战。[14]这些现代进展不仅深化了对流体运动基本规律的理解,也极大地拓展了流体力学在航空航天、环境工程、生物医学等多个领域的应用前景。[15]
2 库恩的范式转换理论对流体力学进步的解释
范式转换理论为理解流体力学的发展提供了一个富有启示性的分析框架。然而,应当注意的是,“范式”及其“转换”在库恩原著及后续研究中本身就存在多重定义与不同诠释方式。[3, 16, 17]笔者在此说的范式,更接近于“流体力学主流支配方程(或研究框架)的核心转变”,而非“在整体世界观、科学共同体研究策略乃至社会—文化层面都出现了新的方法论和概念框架”。库恩认为科学进步是通过范式的转换实现的,而不是简单的知识积累。范式是指某一科学共同体在特定历史时期内共同接受的理论、方法、标准和实践。范式不仅仅是科学理论本身,还包括科学家的研究方法和世界观。正如他所言:“范式是一种包容了某一科学共同体的理论、方法和标准的整体框架”。[3]10在一个共同范式指引下,科学家们进行的研究称为“常规科学”(Normal Science)。常规科学阶段的主要特点是科学家们在现有范式的指导下,解决“谜题”(Puzzles),即细化和扩展现有理论框架,而不是质疑或推翻它。然而,随着时间的推移,科学研究中会出现无法通过现有范式解释的反常(Anomalies)。当这些反常积累到一定程度,便会引发“范式危机”(Crisis)。“科学革命”(Scientific Revolution)正是通过范式危机而启动的。在这一过程中,旧的范式被新的范式所取代,科学观念和研究方法发生根本性转变。库恩用以下文字描述了这一过程:“科学革命的过程,就是科学共同体从旧范式转向新范式的过程,而这通常需要一种不连续的、革命性的转变。”[3]92新的范式能够解释旧范式下无法解决的异常现象,从而得到科学共同体的接受和认可。
库恩还强调了范式的“唯一性”和“主导性”特征。唯一性指的是在特定时期内,科学共同体只会接受一个主流范式,即科学研究的主要理论和方法框架。虽然不同的学者和研究小组可能提出各种各样的理论,但在没有发生范式转换之前,科学共同体通常会集中资源进行某一范式的研究。主导性则意味着范式不仅在理论层面占据主导地位,还在实验方法、技术工具和学术评价等方面具有指导性作用。范式的主导性确保了科学共同体的规范化运作,它为科研活动提供了一个统一的视角和方法论,在解决问题时提供了方向和准则。因此,范式不仅仅是科学理论的集合,更是推动科学研究持续前进的动力源泉。
对流体力学史的考察表明,从牛顿流体理论到欧拉方程,再到纳维-斯托克斯方程的演进,确实展现了科学共同体对流体运动认识的不断深化,但这是否构成库恩意义上的‘革命性’转变,还取决于我们如何定义‘范式’。[18]在流体力学中,牛顿流体理论假设流体应力与流速梯度成线性关系,即粘性力与剪切速率成正比,[8]由此确立了对“牛顿型”流体的基本描述框架。之后,欧拉方程进一步将流体力学带入数学分析的高度,它描述了不可压缩、无粘性流体的运动状态,可以视为牛顿第二定律在理想流体假设下的应用。[16]这种以理想流体模型为起点的范式,的确取得了重要进展;但值得强调的是,欧拉方程从提出之初就并非“未知粘性”带来的意外反常,而是科学家在当时出于数学可处理性、有意忽略黏性影响的简化策略。换言之,人们自始便知道真实流体是有黏性的,只是在可控条件下或特定流动形态中,理想流体模型依然能提供合理近似。
随着工业与工程需求的增加,科学共同体不断积累对黏性流动现象的研究,逐渐发现欧拉方程的适用范围有限,尤其在湍流、边界层流动及黏性占主导时,与实验观测会出现巨大偏差。[11]从库恩的视角来看,这些“偏差”或“局限”虽可以被称作“反常”,但与经典的库恩式反常(如水星轨道进动或迈克尔逊-莫雷实验等)依赖突发或不可预期的新发现有所不同。在流体力学的语境里,欧拉方程对现实的简化是科学共同体预先接受的有意做法,因此这类“反常”更像是对原有模型假设的修正压力,而非彻底颠覆框架的意外发现。[19]
随后,纳维-斯托克斯方程的建立被广泛视为对欧拉方程的进一步完善:它将黏性项纳入方程,成为描述实际流体(包括黏性流体)的标准理论基础。[10]在某种意义上,这使流体力学的应用范围大为扩展,也塑造了现代流体力学研究的理论与实验方法。从“范式转换”的角度来看,如果我们将“范式”理解为“流体力学中最核心的数学模型和研究策略”,那么从欧拉到纳维-斯托克斯确实是一个重要转折:新的方程体系不再忽视黏性效应,并通过数值分析、湍流模拟等现代手段为工程应用提供了关键工具。[17]然而,倘若我们将范式转换限定在“研究共同体根本世界观或方法论的颠覆”意义上,那么这一次转变仍然是在牛顿力学与连续介质力学的基本框架内进行,并未出现像从牛顿力学到相对论力学那样的颠覆性变革。因此,纳维-斯托克斯方程的建立可被视作同一数学物理范式的扩展或‘微观革命’;其“革命性”在于充分涵盖了黏性影响,从而极大拓宽了流体力学的可解释范围。
所以,从牛顿流体理论到欧拉方程、再到纳维-斯托克斯方程的演变过程,既可以被描述为一系列渐进式的理论修正或局部革命,也可以在某些定义下被视为“范式转换”或“革命性”进步。究竟属于哪一种情况,取决于我们对库恩意义下“反常”与“革命”的诠释边界。[20]如果将范式看作“流体力学主流支配方程(或研究框架)的核心转变”,那么这一演变过程确可以说是范式的转换。如果把范式看作“在整体世界观、科学共同体研究策略乃至社会—文化层面都出现了新的方法论和概念框架”,那么这些转变可以被视为在同一整体科学范式(即基于牛顿力学和偏微分方程的连续介质研究策略)内部的渐进深化,而并非库恩所强调的那种‘旧范式被彻底替代’的全面革命。其实,在库恩的科学进步解释模型中还存在一个难以界定的问题,即从反常到危机的临界点在哪里?一个理论要积累多少反常才会引发危机,并引爆科学革命,科学史的无数证据证明,局部的变革同样会引发局部的革命,而且这才是科学进步的常态。即便存在这些缺陷,通过范式转换视角重新审视流体力学发展中的各主要理论转折点,仍然有助于我们理解科学共同体如何定义、接受并不断完善理论模型,从而推动科学理论的丰富与扩展。
3 霍金的模型依赖现实观对流体力学进步的解释
从经典的牛顿流体理论到纳维-斯托克斯方程的提出,再到现代湍流模型的多样化,流体力学的每一次变革都可以视为范式转换的结果。为了更好地理解范式转换的深层意义,可以借用霍金的模型依赖现实观视角进行剖析,以进一步丰富流体力学中模型选择与现实解释的关系。模型依赖现实观是史蒂芬·霍金和伦纳德·蒙洛迪诺(Leonard Mlodinow)基于科学模型如何定义现实而提出的一种科学发展解释模型。它的核心观点是:所有的观察都依赖于模型。“现实的概念并不是独立于图像或理论而存在的。”[4]7没有任何观察是纯粹客观的,因为我们的感官和测量工具本身就是某种模型的体现。例如,我们通过显微镜观察细胞结构,显微镜本身就是基于光学理论的模型。因此,任何观察结果都必须通过模型来解释。霍金与蒙洛迪诺强调科学模型的多样性及其在各自领域内的解释力。[4]44这种观点与传统的实在论(realism)不同,传统实在论认为存在一个独立于我们认知的客观现实,而模型依赖现实观则认为,现实是通过我们的模型来定义和理解的。[4]7模型通过简化和抽象复杂的自然现象,使其易于理解和分析。一个好的模型应当在不失去重要细节的情况下,尽量简化现象。霍金和蒙洛迪诺在《大设计》中指出,一个好的模型能够用少量的任意元素准确描述大量的观察现象。[4]43并且,模型为科学研究提供了一个理论框架,使得不同领域的科学家可以在共同的基础上进行讨论和研究。例如,分子模型为化学和生物学提供了一个理解物质结构和化学反应的框架。
流体力学中的许多理论和模拟方法,尤其是在湍流研究中,都依赖于特定的数学模型来描述和解析流体的行为。这些模型在不同的应用和条件下各自具有不同的适用性与准确性。在模型依赖现实观的框架下,湍流作为流体力学中最复杂、最难预测的现象之一,常常需要通过各种模型来简化其高度非线性、时变的特性。湍流模型例如k-ε模型、大涡模拟和直接数值模拟,都是通过简化湍流的细节来提高计算效率,并在一定程度上与实验数据进行比对,从而提供有用的物理预测(如图1所示)。[21]
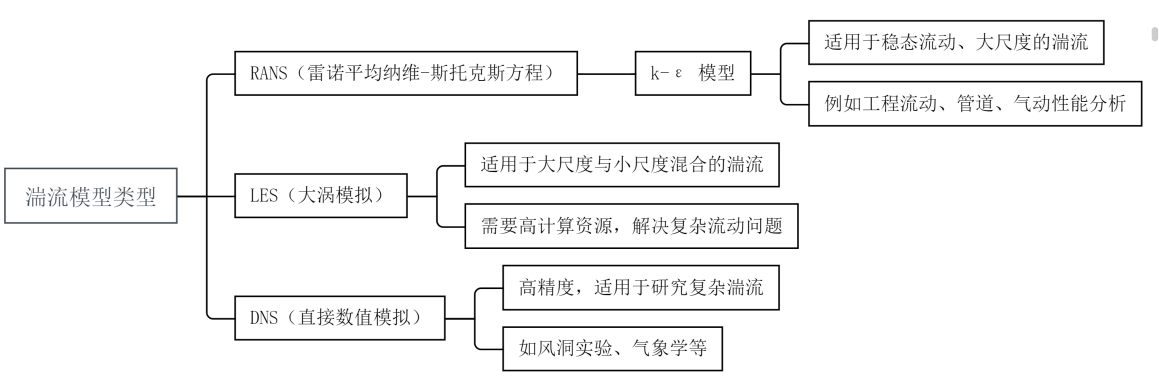
图 1湍流模型类型
Figure 1 Turbulence model type
k-ε模型是一种经典的湍流模型,它通过引入湍流动能(k)和湍流耗散率(ε)来简化流体中对湍流的描述。在此模型中,湍流的各项复杂物理过程被高度简化为对k和ε的方程求解。该模型广泛应用于工程实践中,如空气动力学、汽车设计和建筑流体力学等领域。k-ε模型并不力求完全模拟每一微小的湍流尺度,而是通过整体上的流动特性来达到合理的近似。尽管其准确度有限,尤其在模拟湍流的细节和小尺度涡旋时,k-ε模型在许多工程计算中仍然是一种有效且高效的工具,因为它能够以较低的计算成本实现较为准确的流场预测。[22]
LES则是一种更为精细的湍流模拟方法,它通过直接解析大尺度涡旋的动力学,来更精确地捕捉流体中的重要涡旋结构。与k-ε模型不同,LES通过滤波器对流场进行分解,只模拟大尺度的涡旋,而对小尺度的涡旋进行建模或忽略。这种方法在湍流的预测中,尤其在处理边界层和高雷诺数流动时,提供了更高的准确性。LES通过简化流动的层次,使得科学家能够聚焦于对主要流动特征的理解,而非每一细节的精确模拟。这种方法尤其适用于复杂流动的数值模拟,如飞行器外形设计和发动机内部流动等。[23]然而,尽管LES在精度上优于传统的RANS(雷诺平均Navier-Stokes)模型,其计算成本仍然较高,且在处理极细微的流动特征时仍需要依赖更复杂的亚格子尺度模型。
DNS是最为精确的湍流模拟方法,它通过求解完整的Navier-Stokes方程来模拟所有尺度的涡旋,具有非常高的计算精度。DNS不依赖任何近似或模型,而是通过高分辨率的数值方法完全解析湍流的所有细节。虽然DNS在精度上无可匹敌,但它的计算需求极其高昂,因此仅适用于小规模流动或特定的研究问题。在流体力学的基础研究中,DNS为理解湍流的本质提供了宝贵的数据和理论支持。DNS能够提供最为细致的湍流动态,但它仍然是在特定范围内的现实模型,因为其所能应用的计算资源和实际问题的规模有限。[24]
在流体力学中,尤其是在湍流和复杂流动的模拟中,科学家和工程师常常面临选择合适模型的挑战。霍金理论强调,现实并非独立存在,而是通过我们选择的模型来定义和理解的。因此,流体力学中的模型选择并非依赖于单一“正确”的理论,而是取决于所研究问题的特定需求和精度要求。在湍流模拟中,科学家通常使用不同层次的模型来应对湍流的多样性和复杂性。k-ε模型通过简化湍流的动态过程,只关注湍流动能(k)和湍流耗散率(ε)两个参数。尽管这一模型在许多工程应用中表现良好,但它无法捕捉湍流的所有细节,尤其是在复杂几何形状或高度非定常流动中表现较差。与之相比,大涡模拟(LES)通过解决大尺度的涡旋并对小尺度涡旋进行建模,提供了更精确的湍流描述,能够在细节上更好地匹配实验数据。然而,LES模型需要更高的计算资源,因此其适用性在不同的计算环境下有所限制。更进一步,DNS通过解决流体方程的所有尺度,提供了最精确的湍流模拟,但其计算成本非常高,通常只在小规模、低雷诺数流动或特定研究中使用。通过这些不同层次的模型,科学家能够在精度和计算效率之间做出权衡,选择最合适的模型来解决特定的流体力学问题。
霍金的模型依赖现实观正是强调了科学模型的多样性和适用性。不同的模型根据研究目标、计算能力以及精度要求等因素被选用,它们各自有着不同的适用范围和优劣势。在流体力学中,科学家并不追求某个模型能够解释所有流体现象,而是选择在特定情境下最能揭示物理规律的模型。通过这种方式,流体力学中的模型选择既体现了科学的实用性,也体现了霍金所强调的通过模型来“定义现实”的观点。模型依赖现实观促使我们认识到,不同的模型可以从不同角度揭示现实,而这些模型在实践中并非互相排斥,而是通过选择最适合当前任务的模型来不断推动科学进步。
4 复杂科学理论对流体力学进步的解释融合
不同湍流模型的多样性并不能够完全解释流体力学中的所有复杂现象,因此接下来将探讨复杂科学理论如何进一步补充和扩展这一框架,尤其是在湍流的非线性和多尺度分析方面。复杂系统是指由多个相互作用的组成部分所构成的系统,这些组成部分之间通过复杂的关系和依赖性相互连接和影响。[25]它们的行为通常无法通过单独分析各个组成部分的行为来完全解释。复杂系统可以在多个领域中找到,比如全球气候、生物、社会组织、人脑、生态系统、活细胞等。由于这些系统的组成部分之间的高度互动性,往往表现出独特的行为特征。“非线性”是复杂系统最显著的特征之一,指的是系统的输出与输入之间的关系不成正比,局部的微小变化可能会导致系统整体行为的剧烈变化。例如,生态系统中物种之间的相互作用可能会因为某一物种的微小变化而导致整个生态平衡的改变。[26]“涌现”是指系统整体行为或属性的产生,无法从个别组成部分的行为中直接推导出来。这种现象普遍存在于许多复杂系统中,如社会群体行为、市场经济波动等,这些系统的全局行为往往超出其局部组成部分的简单叠加。例如,大脑中神经元的相互作用生成的意识现象无法单独通过研究单个神经元的活动来解释。[27]“适应性”是复杂系统的另一个核心特性,指的是系统能够根据环境的变化进行自我调整或进化,以适应新的条件。在生物体内,细胞能够根据外部刺激调整其功能,甚至整个生态系统能够通过物种的适应性进化来应对环境变化。适应性常常伴随着反馈机制,形成反馈循环。反馈循环包括正反馈和负反馈,其中正反馈放大系统中的变化,可能导致系统不稳定,而负反馈则调节系统,帮助其维持稳定状态。总之,复杂系统的非线性、涌现、适应性和反馈循环等特性使得它们的行为常常难以预测,要求科学家采用新的理论和方法来分析和理解这些系统的整体行为。
流体力学中的复杂性主要体现在湍流现象的多尺度和多变量相互作用上。[28]湍流是流体力学中最具挑战性的研究对象,它由多种尺度的流动结构组成,从大尺度的漩涡到小尺度的分子运动,每个尺度之间存在复杂的相互作用。湍流中的流动不仅涉及速度和压力等变量,还包括温度、密度、浓度等多种物理量,这些变量之间相互作用,形成了极其复杂的动态系统。例如,大尺度的涡旋会影响小尺度湍流结构的形成,而小尺度的能量传递又对整体湍流状态产生反馈作用。由于这些多尺度、多变量的相互作用,湍流不仅难以通过传统的解析方法精确描述,还需要通过数值模拟和近似模型来研究。
此外,非线性动力学和混沌理论为流体力学中的复杂性提供了另一层次的理解。湍流的非线性特性使得其行为具有高度的敏感性和不可预测性,即使是微小的初始条件变化,也可能导致流动行为的巨大差异,这正是混沌现象的典型特征。在流体动力学中,湍流常常表现出对初始条件的强烈依赖,且其流动状态可能迅速变化,这使得预测和控制湍流变得极为困难。即便采用高精度的数值模拟方法,如DNS,也仅能在有限的计算资源下对流动的某些方面进行模拟。由于混沌流动的普遍存在,传统的流体力学理论在处理复杂流动问题时面临巨大的挑战,科学家必须依赖统计学方法和经验模型来进行大规模流动的预测。[29]
除了库恩和霍金的理论外,引入复杂系统理论来解释流体力学的演进是非常必要的。因为复杂科学为理解流体力学中的动态演变提供了新的视角和工具。库恩的范式转换理论强调,科学进步往往通过范式的革命性转换来实现,然而,在流体力学的历史演进过程中,复杂系统理论为这一转变提供了丰富的理论基础和实践指导。复杂系统理论通过揭示流体中的非线性、多尺度、多变量的相互作用,帮助我们深入理解传统模型无法解决的复杂现象。例如,在湍流的研究中,传统的流体力学模型往往无法精确捕捉到多尺度的相互作用和涡旋的形成过程,而复杂系统理论中的“自组织”和“涌现”概念则为我们提供了更为系统化的解释框架。通过对涡旋结构的理解,复杂系统理论帮助科学家们识别了湍流中不同尺度之间的能量传递机制,促进了新模型的提出。
复杂系统理论还对霍金的模型依赖现实观提供了进一步的补充,尤其是在模型的多样性和适应性方面。霍金提出,现实并非单一客观的存在,而是通过科学模型来定义和理解的。不同的科学模型应根据具体的研究问题和实验条件来进行选择和优化。然而,复杂系统理论进一步深化了这一观点,强调模型不仅需要多样化,还应具有适应性,能够根据不同的环境和条件变化做出调整。在流体力学中,湍流模拟方法就是一个典型的例子。对于低雷诺数流动,DNS方法能够精确模拟每一个尺度的涡旋和流体结构,但它计算量巨大,仅适用于较简单的流动情况;对于高雷诺数流动,LES方法通过对小尺度涡旋进行模型化,能够在较大计算规模下进行模拟。k-ε模型虽然在大规模工程应用中广泛使用,但它过于简化,不能捕捉湍流的微观特性。在这种情况下,模型的多样性和适应性尤为重要,复杂系统理论的引入使得科学家能够根据实际需要选择合适的模型。
5 库恩、霍金与复杂科学理论关于进步解释的互补性分析
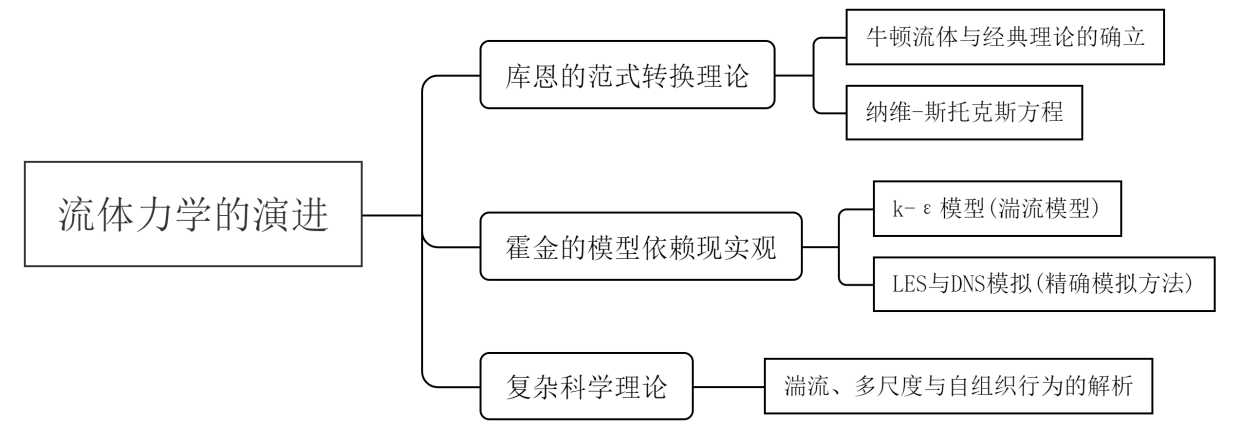
图 2流体力学演进的三种理论分析示意图
Figure 2 Three theoretical analysis diagrams of fluid mechanics evolution
综合库恩的范式转换、霍金的模型依赖现实观以及复杂科学的理论,分析它们如何共同作用,促进对流体力学进步的更深刻理解(如图2所示)。通过对这些理论的互补性分析,我们将看到,范式的转换不仅仅是理论更新,还是在更广阔的理论框架中,结合模型优化与复杂性处理来实现流体力学进步的多重解释。这些理论的整合为理解科学进步提供了更加全面的视角,尤其对现代流体力学的应用和优化具有重要启发。
第一,在解释科学进步中,库恩和霍金有不同的侧重点。关于模型的多样性,霍金的模型依赖现实观强调科学模型的多样性和实用性,库恩则强调科学范式的唯一性和主导性。霍金认为,科学模型是我们理解和描述现实的工具,并且多个模型可以同时存在,只要它们能够有效地解释和预测观测结果。他在《大设计》中写道:“模型依赖现实观表明,当存在两个或更多种根据已有数据构建的模型时,我们不能断言其中的哪一个更真实,而应该使用那些足够有效的模型。事实上,不同的理论可能在描述同一现象方面都很成功,只要这些理论能够在它们各自适用的范围内预测观测结果。”[4]46他们的观点反映了一种实用主义的科学哲学态度,即认为科学模型的价值在于其解释和预测能力,而非其与某个绝对真理的符合度。这与科学哲学家波普尔对理论与真理的论述殊途同归,在波普尔那里,理论就是解决问题的工具,通过猜测与反驳而逐渐趋近于真理,但理论并不代表真理。库恩则认为,在常规科学的阶段,科学共同体通常遵循一个单一的、普遍接受的范式,这个范式定义了科学研究的标准、方法和问题的合法性。这种范式的唯一性和主导性是常规科学运行的基础,它指导科学家们如何进行实验、解释数据和验证理论。
第二,在科学理论的验证方式上,库恩认为科学理论通过异常现象的累积导致危机和革命,霍金则看重实验验证和观测数据的适应性。在库恩看来,科学理论的验证不仅仅通过累积数据和逐步改进实现的,而是通过一系列革命性的变化,这些变化通常是由异常现象的累积导致的,最终导致科学共同体对现有范式的信任危机:“常规科学活动中不可避免地会出现与理论预测不符的现象。当这些异常累积到一定程度,无法被现有的科学理论解释时,它们就会引发所谓的‘危机’。”[3]82霍金则认为,科学进步是通过选择最能准确预测和解释观测数据的模型来实现的:“一种科学理论或模型被接受的程度取决于它对观测结果的解释能力,以及它在新的实验和观测中的预测准确性。”[4]72霍金和蒙洛迪诺进一步阐述了科学模型的选择标准,强调这种选择是基于实用性和实验验证:“我们选择使用哪种模型并不是基于哪个更真实,而是基于哪个模型能更有效地解释我们所看到的现象,并能准确预测未来事件。”[4]57这两种方法展示了科学理论验证在哲学上的深刻差异:库恩的视角强调理论在面对新的挑战时的脆弱性和范式的转换,而霍金则看重理论的实际应用、适应性和通过实验得到的验证。这种差异反映了对科学进步本质的根本不同理解。
而复杂系统之所以能补充库恩和霍金的理论,有两个理由。其一,它不仅理解现有模型的局限性,还揭示了模型优化的动力机制。复杂系统中存在多层次、多尺度的相互作用,这意味着不同尺度的物理过程对整体系统的影响是不同的。湍流中的能量传递、涡旋结构的演化等过程往往在不同尺度上相互交织,传统的简化模型无法全面捕捉这些交互作用的细节。模型优化因此不仅仅是对模型参数进行调整或引入新的方程,而是对模型结构本身的革新。[29]在这一过程中,科学家需要根据研究对象的实际需求,选择合适的模型框架,并根据观测和实验结果进行持续调整。这与库恩的范式转换理论高度契合,范式的转换不仅仅是理论的更替,还是对科学工具和方法的不断优化与革新。复杂系统理论通过提供多尺度和适应性框架,使得流体力学中的模型优化能够更好地应对不同应用场景的挑战。在工程科学中,随着大数据技术和计算能力的提升,越来越多的实时流体模拟能够结合实验数据进行反馈和优化,使得模型更加灵活和适应不同的物理环境。例如,在空气动力学的研究中,LES方法通过精细的网格划分和大涡的追踪,能够实现对飞机机翼周围复杂流动的高效模拟,这为新型飞机设计提供了更高效的优化工具。[28]
其二,复杂系统的“涌现”和“自组织”特性,尤其是在处理大规模、动态交互的系统时,为工程科学提供了新的解释框架。[30]在工程科学中,系统的复杂性往往超出传统线性思维的范畴,涌现特性揭示了局部的简单互动如何导致全局性、非线性行为的发生。例如,在交通工程中,虽然单个汽车的行驶行为相对简单,但当这些汽车在复杂的道路网络中相互作用时,就可能出现交通堵塞、堵车波动等复杂现象。传统的交通流模型往往只能描述均匀的、线性的流动,而无法有效预测因车流密度变化而引起的交通涌现现象。通过引入复杂系统中的涌现理论,工程师能够利用智能交通系统(ITS)设计出更为高效的交通管理策略,预测并缓解潜在的交通堵塞,从而提高交通系统的整体效率。
自组织是复杂系统的另一重要特性,它描述的是系统在没有外部控制的情况下,通过内部的相互作用自发形成有序结构或模式。[31]在工程科学中,自组织不仅解释了自然界中许多复杂现象的形成,也为人工系统的设计提供了新的思路。例如,智能制造和分布式能源系统的设计就充分利用了自组织的概念。在智能制造领域,各个生产单元通过局部信息交换和自适应控制,能够在不依赖中心控制的情况下实现全局优化。例如,工业4.0中的物联网(IoT)系统允许各个生产设备在网络中自主协作,通过实时数据共享和智能决策优化生产流程。自组织的理念同样适用于分布式能源系统,通过利用本地能源生成和存储单元的自主协调,减少对传统集中式电网的依赖,从而提高系统的灵活性和可持续性。在这些应用中,复杂系统的自组织特性促使工程师跳出传统的中央集权式设计思维,转而关注局部交互与全局优化之间的平衡。
6 结论
在库恩看来,科学进步并非仅仅依赖知识的线性累积,而常常通过对主导理论框架的“范式转换”而发生转变。在流体力学的发展历程中,从经典的牛顿流体理论到纳维-斯托克斯方程的建立,的确体现了研究共同体对核心假设与方法的重大修正与拓展。随着计算能力和实验技术的不断提升,诸如湍流大涡模拟(LES)与直接数值模拟(DNS)等新方法的出现,也进一步推动了研究边界的扩张。若从库恩的视角审视这些关键突破,它们不仅意味着技术进步,更是对既有范式的持续挑战与重塑,因而在某种程度上可被视为带有“革命性”特征的学科演变。霍金的模型依赖现实观则为流体力学的理论选择和应用提供了更加灵活和多元的思考方式。霍金提出,科学模型并非简单地反映现实,而是通过特定的理论框架来解释观察结果。不同的模型,如k-ε模型、LES和DNS,依据问题的规模和研究的细节需求,在不同的应用场景中展现了其独特的适用性和局限性。复杂科学理论则通过“涌现”“自组织”概念,揭示了流体力学中多尺度、多变量相互作用的本质。这一理论框架帮助我们理解了湍流等复杂流动现象背后的规律性,推动了新的理论和模拟方法的开发。流体力学中的涡旋结构、能量传递机制等现象,往往无法用传统的线性思维来解释,复杂系统理论提供的非线性分析和多尺度建模方法,正是解决这一难题的关键。在科学范式转换的过程中,这种观点支持科学家们探索和采纳新的或改进的模型来解释新发现的现象,无需彻底抛弃旧有的理论。这种适应性和包容性使得科学研究能够在保持连续性的同时,快速响应新的证据和观点。诚如美国科学哲学家达德利•夏佩尔(Dudley Shapere,1928-2017)所言:“要求放弃一些已经证明在科学中具有极大解释价值的原则,所以人们以极其谨慎的态度来看待它。放弃多年积累的进步,以支持一个完全新的和相对来说未经考验的系统(这个系统仅仅是打算处理旧理论已证明是能够处理的事实的一小部分)这将是十分危险的。”[32]
库恩、霍金和复杂科学的理论,不仅为理解流体力学的学术发展提供了深刻的哲学基础,也对我们全面理解科学/工程提供了多元视角。任何进步都是复杂的,只有多重解释我们才能真正理解进步的丰富内涵,就如同盲人摸象,每一个角度都有合理性,但是仅凭一个视角我们是无法全面了解真实的大象,只有整合多个视角,大象的完整形象才会呈现出来。那种传统的、线性的、简单的、片面的解释科学/工程进步的认知模式恰恰是造成我们误解进步的源头,流体力学的发展史很好地说明了这种情况。
参考文献
[1] White F. Fluid Mechanics 8th Ed., 8th Editio [M]. McGraw Hill, 2016.
[2] Batchelor G K. An introduction to fluid dynamics [M]. Cambridge university press, 2000.
[3] Kuhn T. The Structure of Scientific Revolutions [M]. University of Chicago Press, 1996.
[4] Mlodinow S H L. The Grand Design [M]. Bantam Books, 2010.
[5] 于海明, 邓杰文, 周岭. 流体力学 [M]. 2022.
[6] Quarantotto D. Aristotle's Physics Book I [M]. Cambridge University Press, 2018.
[7] Galilei G. Discourses and mathematical demonstrations relating to two new sciences [J]. Leiden (1638), 1954.
[8] Newton I. Philosophiae naturalis principia mathematica [M]. G. Brookman, 1833.
[9] Bernoulli D. Hydrodynamica [J]. Dulsecker Consultable en ligne http://imgbase-scd-ulp u-strasbg fr/displayimage php, 2016, 1738.
[10] Stokes G G. On the theories of the internal friction of fluids in motion, and of the equilibrium and motion of elastic solids [J]. 2007.
[11] Navier C L. Mémoire sur les lois de l'équilibre et du mouvement des corps solides élastiques [M]. 1827.
[12] Anderson J D, Wendt J. Computational fluid dynamics [M]. Springer, 1995.
[13] Adrian R J, Westerweel J. Particle image velocimetry [M]. Cambridge university press, 2011.
[14] Duraisamy K. Perspectives on machine learning-augmented Reynolds-averaged and large eddy simulation models of turbulence [J]. Physical Review Fluids, 2021, 6(5): 050504.
[15] 张伟伟, 寇家庆, 刘溢浪. 智能赋能流体力学展望 [J]. 西北工业大学航空学院, 2021, 第42卷(第4期): 26-71.
[16] Anand G, Larson E C, Mahoney J T. Thomas Kuhn on paradigms [J]. Production and Operations Management, 2020, 29(7): 1650-7.
[17] Kuhn T S. Second thoughts on paradigms [J]. The structure of scientific theories, 1974, 2: 459-82.
[18] Orman T F. Paradigm” as a central concept in Thomas Kuhn’s thought [J]. International Journal of Humanities and Social Science, 2016, 6(10): 47-52.
[19] McNamara D. Paradigm lost: Thomas Kuhn and educational research [J]. British educational research journal, 1979, 5(2): 167-73.
[20] Jones C A. The modernist paradigm: the artworld and Thomas Kuhn [J]. Critical Inquiry, 2000, 26(3): 488-528.
[21] 闻建龙主编;王贞涛, 王晓英参编;罗惕乾主审. 工程流体力学 [M]. 2023.
[22] Launder B. Lectures in mathematical models of turbulence [Z]. Academic Press. 1972
[23] Sagaut P. Large eddy simulation for incompressible flows: an introduction [M]. Springer Science & Business Media, 2005.
[24] Moser R D, Kim J, Mansour N N. Direct numerical simulation of turbulent channel flow up to Reτ= 590 [J]. Physics of fluids, 1999, 11(4): 943-5.
[25] Bar‐Yam Y. Multiscale variety in complex systems [J]. Complexity, 2004, 9(4): 37-45.
[26] Mitchell M. Complexity: A guided tour [M]. Oxford University Press, 2009.
[27] Holland J H. Complexity: A very short introduction [M]. OUP Oxford, 2014.
[28] Cant S. SB Pope, Turbulent Flows, Cambridge University Press, Cambridge, UK, 2000, 771 pp [J]. Combustion and Flame, 2001, 125(4): 1361-2.
[29] Lesieur M, Metais O. New trends in large-eddy simulations of turbulence [J]. Annual review of fluid mechanics, 1996, 28(1): 45-82.
[30] Bar-Yam Y. Unifying principles in complex systems [Z]. New York: Springer. 2003: 380-409
[31] Holland J H, Sigmund K. Hidden order: how adaptation builds complexity [J]. Nature, 1995, 378(6556): 453-.
[32] 达德利.夏佩尔. 理由与求知——科学哲学研究文集 [M]. 上海: 上海译文出版社, 2001.
作者简介:
叶菲楠,上海交通大学科学史与科学文化研究院博士研究生。研究方向为科学思想史。
李侠,上海交通大学科学史与科学文化研究院教授,研究方向为科学哲学。
【博主跋】这篇小文章是小叶同学去年写的,折腾快一年了,我查看修改记录,我这边最后一次修改是今年1月9号,后来她又修改了几次。现在发文章太难了,我一直觉得这篇文章的品相很不错,应该可以发一篇C刊,怎奈现在编辑部几乎都在追热点,基本上不录用那些与热点无关的文章,我觉得这很不好,其实很多热点就像流行性感冒一样,一阵风过后,人们又在等待下一个风口和热点,难道我们就不能踏实地做点老问题研究吗?很多看似传统的老问题其实我们并不了解,也没有彻底解决,反而需要几代人慢慢推进,直到把那个问题真正搞清楚了,我觉得这才是真正地推进知识的进步。现在这篇文章发在《工程研究》2025(3)上【知网上已经登出网络版,具体出版刊号以纸刊为准】,发表时文章题目略有改动,这是原稿,再次感谢王大洲教授,合作愉快,是为记。
说明:文中图片来自网络,没有任何商业目的,仅供欣赏,特此致谢!
2025年6月29日于南方临屏涂鸦
转载本文请联系原作者获取授权,同时请注明本文来自李侠科学网博客。
链接地址:https://wap.sciencenet.cn/blog-829-1491660.html?mobile=1
收藏

