 精选
精选
溶剂化电子
一直想学习一下这方面知识,主要是希望清楚二个问题,一是电子能否在水溶液中长时间稳定存在,二是含有电子的水是否可能具有生物学作用。当然回答上述问题首先要明白的是这种物质类型的特征知识。最近有关于这种电子的最新研究,似乎没有说清楚来源,正好进行整理。
The Hydrated Electron | Annual Review of Physical Chemistry (annualreviews.org)
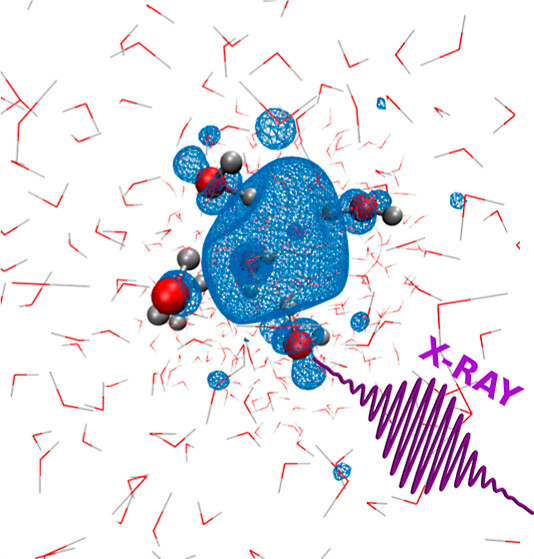
对水进行放射性分解所涉及的事件时间尺度,从最初的电离事件的几阿秒(attoseconds),到形成离子和自由基如OH⁻、H₃O⁺和OH•的几飞秒(femtoseconds)和皮秒(picoseconds)。水放射性分解还产生了大量的次级电子作为副产品,特别是当水与高能辐射(α粒子、β、γ或X射线)相互作用时。 在液态水中,这些电子逐渐失去能量并在与周围介质碰撞时减速,通过激发或电离其他分子来扩散辐射引起的损伤。其中一些电子可能被介质中的分子捕获,而其他电子则继续减速,直到它们有能力极化周围的水分子。为了应对这种极化,水分子会定位自己以围绕电子创建一个笼子,导致形成溶剂化电子(水合电子)。在其形成后的几皮秒内,溶剂化电子将重组。这种看似简单的物种——一个被水分子包围的单个电子——的基本而迷人的性质自其发现以来引发了众多研究,揭示了包括放射治疗、 核反应堆腐蚀、污染物降解等广泛领域的重要影响。
由于实验表征和理论建模的挑战,水合电子的结构一直是激烈争论的主题。(10) 共识是将电子置于由4-6个水分子创建的空腔中心,每个水分子都用它们的一个氢原子与电子配位。追踪这个物种的诞生同样具有挑战性,因为水合电子前体的寿命很短,这需要超快技术。因此,电子溶剂化过程的许多关键方面仍然不清楚。未解决的问题包括溶剂化时间尺度,研究报告的值范围从几百飞秒到2皮秒不等,以及之前的电离机制的影响,或者水合电子直接前体的具体性质,等等。这种普遍缺乏共识的根源在于使用光学技术时难以区分振动和电子响应的固有困难。(20) 尽管水合电子对X射线相当透明,但通过计算K边X射线吸收光谱(XAS),Li等人最近展示了X射线可以用来探测水合电子周围空腔的存在。他们建议使用时间分辨X射线吸收光谱(trXAS)来追踪水合电子溶剂化结构的变化,利用XAS的高结构敏感性。X射线已经证明了它们在揭示液态水中局部瞬态结构方面的特殊适用性。但到目前为止,X射线光谱学对溶剂化电子及其溶剂化壳的实验应用仍然缺失。在本文中,我们报告了借助trXAS形成的空腔最直接的证据。多亏了一种复杂的全电子方法,我们进一步加深了我们对水合电子及其环境在空腔形成过程中如何相互影响的理解。
本研究展示了电离液态水的时间分辨X射线吸收光谱,并证明了OH自由基、H₃O⁺离子和溶剂化电子都留下了独特的X射线光谱特征。特别是,这使我们能够通过一种关注溶剂化电子附近氧原子的电子响应的工具来表征电子溶剂化过程。我们的实验结果得到了从头计算的支持,确认了溶剂化电子被困在一个空腔中的形成。我们展示了溶剂化动力学受到水中存在的随机结构波动幅度的支配。因此,溶剂化时间对温度和电子注入水中的特定方式都非常敏感。
Sopena Moros A, Li S, Li K, Doumy G, Southworth SH, Otolski C, Schaller RD, Kumagai Y, Rubensson JE, Simon M, Dakovski G, Kunnus K, Robinson JS, Hampton CY, Hoffman DJ, Koralek J, Loh ZH, Santra R, Inhester L, Young L. Tracking Cavity Formation in Electron Solvation: Insights from X-ray Spectroscopy and Theory. J Am Chem Soc. 2024 Feb 7;146(5):3262-3269.
溶剂化电子
溶剂化电子是一个自由电子的溶液,并且是可能的最小阴离子。溶剂化电子广泛存在,尽管很难直接观察它们,因为它们寿命很短。碱金属在液氨中的溶液呈不同深度颜色是由于溶剂化电子的存在。溶剂化电子的讨论集中在它们在氨中的溶液,氨溶液可以稳定数天,但溶剂化电子也存在于水和其他溶剂中——事实上,在任何介导外球电子转移的溶剂中。溶剂化电子的实际水合能可以通过使用质子在水中的水合能结合脉冲辐解实验的动力学数据来估计。溶剂化电子与原子氢形成酸碱对。(是否强碱性电解水含有这种酸碱对,或者可以稳定存在?)
Herbert J M, Coons M P. The hydrated electron[J]. Annual review of physical chemistry, 2017, 68: 447-472.
1.1. 溶剂化电子的研究历史
溶剂化电子是一个比较古老的学术问题。早在二个多世纪前,Humphry Davy首次观察到了后来被理解为溶剂化电子的现象,并在其1808年的实验室笔记中描述了当钾晶体在氨气存在下加热时所见到的“美丽的金属外观”和“细腻的蓝色”(1)。继氨液化之后,Weyl在1864年(2)注意到钠/氨混合物的蓝色,并将其归因于形成化学化合物NaNH3。这一观点一度盛行,直到1908年Kraus提出了令人信服的反对证据(3),这些实验最初旨在测试电子是金属导电中的电荷载体的观点(4)。Kohlrausch(5)早已确定了电解质溶液中溶解离子作为电荷载体的存在,但在Kraus看来,“对固态物质的了解...还远远不够,我们无法确定当电流通过金属时所涉及的具体过程的性质”(4),他推测,将金属溶解在非导电溶剂中的溶液可能提供更简单的系统来测试金属电导的理论。
为此,Kraus测量了溶解在液氨中的碱金属溶液的电导率,并且在他1908年的第一篇论文中(6, p. 1332),他提出电荷载体是“被氨包围的电子”,即通过Na⇇Na++e−解离平衡形成的溶剂化电子。这一推论显得更为深刻,因为电子作为阴极射线管中电荷载体的性质大约在十年前才被确定(7),而Kraus的1908年论文比Millikan的油滴实验的发表还要早(8)。
在Kraus提出他的假设几年后,Gibson和Argo(9, 10)测量了碱金属和碱土金属溶解在液氨和有机胺中的溶液的光学吸收光谱。这些溶液都呈现出强烈的蓝色,并且在给定溶剂中最大吸收的波长与金属的种类无关(10)。基于金属色散的经典理论,Gibson和Argo表明,如果假设溶液中只有未离解的金属存在,那么吸收截面与电导率数据是无法调和的(9)。由此,溶剂化电子作为一个独特的化学物种的概念得以确立。这些实验早于“新”量子理论的发展,但到了1946年,已经有人提出碱金属溶液在氨中的光学光谱源于粒子在准球形溶剂空腔中的s→p激发(11)。这一概念后来得到了进一步的阐述(12),并由Jortner及其同事为水合电子(13)进行了调整。
本综述专注于水合电子水合电子的特定案例,关于早期实验的详细历史记录可以在其他地方找到(14–16)。简要地说,早在1952年就有人提出这样的物种可能是水溶液辐射分解的副产品(17),但是碱金属与水的反应不会产生任何可见的颜色变化,这最终是由于水合电子在中性水中的寿命大约为300微秒,当以低浓度生成时可能会更短(18)。水合电子可以通过脉冲辐射分解水溶液来产生(18),就像1962年首次测量光学光谱的原始实验(19);通过对水溶液的超声波分解(20);通过双光子激光激发液态水;或者通过适当的电子供体进行光电离,例如,通过接触I−(aq)或CN−(aq)的电荷转移到溶剂激发态(21–23)。自从首次实验检测到水合电子以来的50多年里,它被认为是水辐射分解时形成的主要自由基之一(14, 24, 25)。
理论上试图理解水合电子的详细结构几乎与首次测量光学光谱一样久远。早期的模型本质上是连续的或半连续的(13, 26–29),假设电子存在于液态水结构中的排斥体积中,这与水合电子的部分摩尔体积的实验测量结果一致(30, 31)。在1970年代,对电子顺磁共振(ESR)光谱的分析似乎证实了这一点(32)。同样的图景后来也从使用单电子(赝势)模型的原子模拟中出现(33, 34),最后是基于密度泛函理论(DFT)的第一性原理计算(35–37)。因此,这种空腔模型的水合电子已成为常规范式,尽管偶尔并且持续地存在争议(38–42),如第4节所述。
在1980年代,有限簇合物类似物的水合电子在分子束中被创建(43),对这些簇进行质量选择并对其进行光谱学询问提供了另一种理解水如何容纳额外电子的途径。对簇光谱学的解释一直存在争议(44–46),并在第2节中讨论。在第3节中讨论了液态水中水合电子的光谱学研究。
1.2 溶剂化电子的化学意义
虽然本综述主要关注结构、光谱和能量方面的考虑,但水合电子作为水相化学反应中的一种强还原剂的重要性不容忽视。图1展示了水辐射分解中的一些早期事件(47),其中电离辐射产生了三种主要自由基:H、HO和水合电子。后者在皮秒时间尺度上热化,比真空能级低约3.5 eV,其形成和消耗可以通过归属于水合电子占据的空腔排斥体积内的s→p激发的强烈吸收来监测。
尽管涉及水合电子的一些反应是扩散限制的,但许多反应表现出1-8 kcal/mol的活化能(24),这表明动力学受反应伙伴物种上空轨道可用性的控制。然而,即使是最简单的反应。
分子层面的机制并不总是清楚的。虽然长期持有的观点是水合电子总是通过电子转移机制反应(14),但最近对小水簇中反应(1)的DFT模拟表明,它可能通过将质子转移到水合电子空腔中发生(48, 49)。这需要同时对质子和电子水合壳进行显著重排,包括对未配对电子的显著扭曲,这有助于反应,但伴随着两个亲水反应物脱溶剂化的能源惩罚。也许令人惊讶的是,反应1比H+(aq) + HO−(aq) → H2O进行得更慢,人们可能会预期围绕两种离子的水合壳有类似的破坏,也比水合电子 + HO → HO−(aq)进行得更慢。这些例子表明,并非所有的水合电子化学都应该用电子转移的概念来概念化。
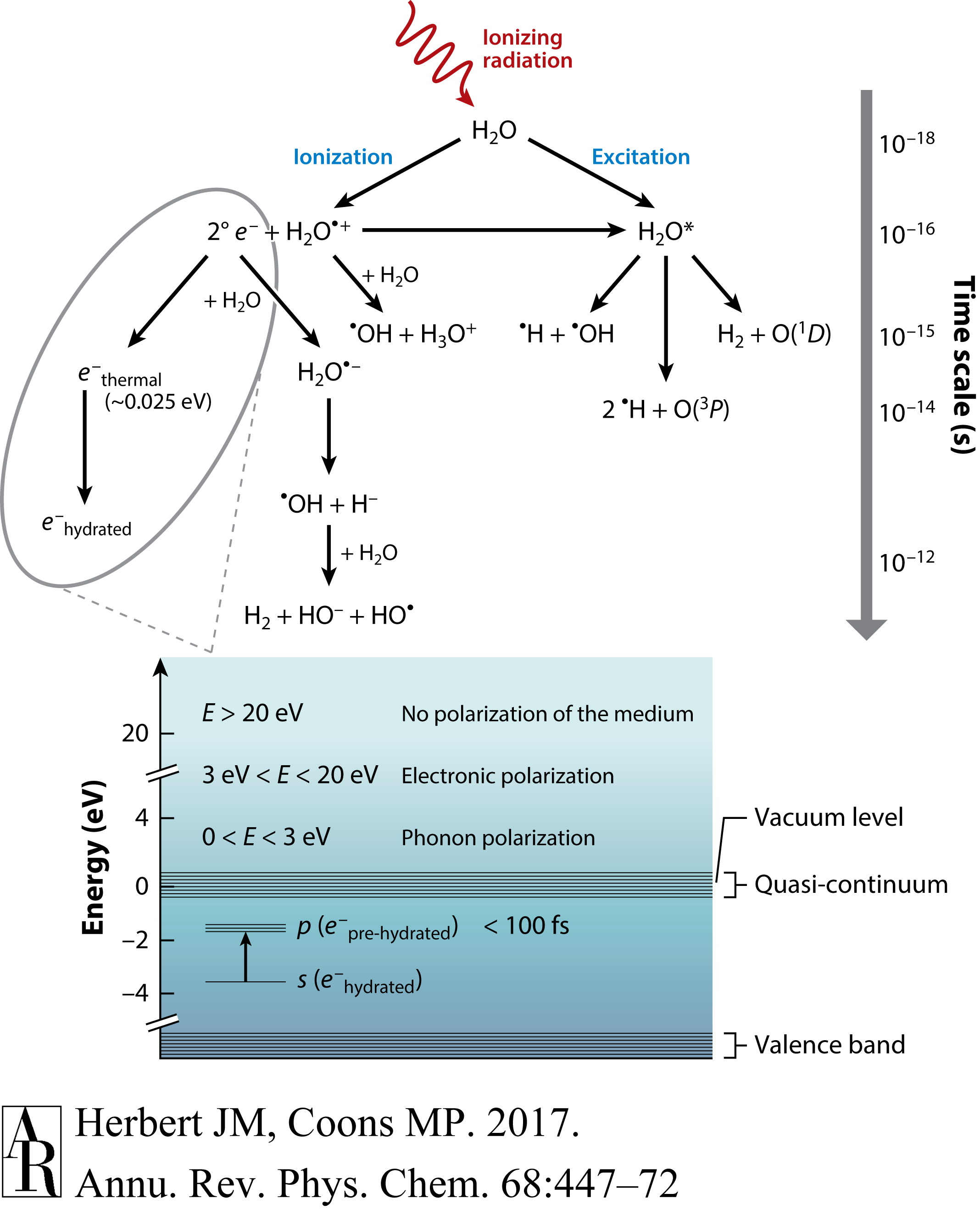
图1 水辐射分解的示意图,其中电离辐射产生自由基中间体水合电子、H和HO。图中下半部分描述了体相水中水合电子的能级图。
 1
1
电离辐射的直接吸收可以在DNA中诱导产生致突变的损伤;然而,实际上在水中产生的次级物种,如水合电子,才是造成大部分损伤的原因(50–52)。动能在3-20 eV范围内的电子可以在真空中诱导单链和双链断裂(53),损伤分布峰值在10 eV左右,这表明核苷酸的核心激发共振可能参与其中(52, 53)。此外,能量低至0.1-2.0 eV的电子,远低于DNA的估计电离阈值7.0-10.5 eV(53),也能诱导DNA中共价键的断裂。在提出的机制中(54),一个电子被DNA碱基的π轨道捕获,形成一个阴离子形状共振,入射电子的过剩动能诱导额外的π→π激发:e− + (π)2 → (π)1(π*)2。结果得到的(π)1(π*)2态沿着糖-磷酸键坐标是解离的。已经观察到,水溶液中的电子在超快时间尺度上在DNA中形成阴离子共振(55),随后在几皮秒内发生DNA降解。尽管在气相中电子附着到核苷酸上在能量上是不利的,但只需添加几个溶剂化水分子就能导致核苷酸和核苷酸的绝热电子亲和性显著增加(>1 eV)(56, 57)。因此,人们可能会预期在水环境中电子附着到DNA上会被增强。
2. 水簇阴离子
有限大小的簇首次在1981年的分子束中产生(43),自那时起,通过光电光谱学(58-60)对多达N=200的簇进行了研究,通过振动光谱学(61, 62)对多达N=50的簇进行了研究。簇,尤其是小簇,适合进行精确的电子结构计算,这可以通过定位那些能够复制实验光谱的异构体来阐明电子结合模式。因此,簇研究的一个主要目标是在分子层面上理解水网络是如何容纳额外的电子的,以及随着簇从几个分子演变成可能类似于水合电子的东西时,这种容纳是如何变化的。然而,即使对于像这样的小簇,理论上对实验光谱的指派也已证明是具有挑战性的,并且对于更大的簇来说仍然是一个悬而未决的问题。如下所述,潜在的异构体数量如此之多,以至于人们可能会合理地质疑仅仅编录异构体的计算研究是否真的有用。对更大簇的研究可能会对凝聚相有所洞察,但这可能需要放弃将观察到的光谱特征分配给不同结构异构体的概念。我们用(H2O)−6的案例研究来说明这个问题的复杂性,然后解决关于较大异构体光电光谱解释的长期争议,特别是表面结合与内部结合的簇异构体的存在。
2.1. 小簇:与从头开始计算的直接比较
(H2O)−6结构的解释不断演变,这提供了一个难以仅基于垂直电子结合能(VEBEs)来指派簇异构体的例子。1996年首次测量了(H2O)−6的VEBE光谱(63)。测量到的VEBE光谱(图2)包括两个主要峰,同位素替换揭示这是两个不同异构体的带起源。基于各种(H2O)−6异构体的从头计算VEBE,Kim等人(64)立即将此光谱归因于图2a中所示的两个异构体。计算得到的VEBEs与实验值相差<0.1 eV,并且这一指派与早期关于表面结合和内部结合簇异构体存在的猜测(58)一致。然而,这一指派很快被同一作者(65)修正,基于更彻底的搜索,改为由图2b中所示的三个不同异构体组成。对于这个新的指派,包括振动加宽效应在内的VEBEs模拟分布与实验半定量一致,如图2所示。然而,Jordan和同事(66)后来使用更高质量的基组重新审视了计算,这使得VEBEs改变了≈0.15 eV,并最终得出结论,该光谱可能起源于图2c中所示的线性异构体。几年后,Kim和同事(67)使用更高级别的理论重新计算了VEBEs,并将光谱重新指派给图2d中所示的两个异构体。

图2(左)实验测得的(H₂O)₆谱图(黑色),与基于从头计算的计算谱图(红色)叠加。峰的假定归属根据右侧描绘的簇异构体进行标记。
这个例子突显了仅基于VEBEs来指派结构异构体的固有困难,但振动光谱可以提供额外信息。Arn(H2O)−6簇的振动预解离光谱(66, 70, 71)显示了一个强烈的O–H伸缩双峰,相对于气相H2O红移了多达∼400 cm−1;见图3a。这一特征部分用于将线性异构体指派给图2中的VEBE光谱,因为线性异构体在O–H伸缩区域复制了强烈红移的双峰(66)。
然而,通常情况下,振动光谱来自多个具有强烈重叠振动特征的异构体;这些可以通过利用附着的Ar原子数量变化时异构体比率的变化来彼此分离(70, 71)。图3b,c中显示了两个不同异构体的去卷积光谱,其中它们已基于使用DFT计算的比例谐波频率指派给异构体。尽管在同一级别的理论计算的VEBEs远大于实验值,但从头计算振动光谱与实验非常吻合,原因是已知的(72)。不幸的是,这意味着很难使用一致且计算上可行的理论方法来同时处理振动和光电子光谱,尤其是当簇大小远远超过N=6时。最终,光电子光谱的6Af/6Bd指派(图2d),最初由Lee等人(67)在2003年提出,并在后来的振动预解离光谱指派中再次确认(70, 71),已成为共识,即使是在对势能面进行更彻底搜索之后(73, 74)。然而,这一共识的形成花了10年时间,并且在首次报道(H2O)−6的光电子光谱15年多后才出现。
对于稍大的(H2O)−7簇,比例谐波频率同样适用于几种具有相当相对能量但氢键排列细节不同的结构(75)。随着簇大小的增长,试图做出明确的异构体指派很快就变得不可能,或许人们所能做的最好的事情是指派与特定振动特征相关的局部几何结构(75, 76)。(H2O)−6中强烈红移的O–H伸缩特征就是一个很好的例子,它已被指派给一个处于双氢键受体(AA)配置的水分子(见图3b)。在AA水分子中,O–H部分不参与与其他水分子的氢键结合,两者都自由地与未配对电子形成氢键。AA水分子上O–H伸缩模式的大幅红移是由于未配对电子渗透到σ*(OH)轨道(77)。AA水分子的振动特征在至少到N=21的振动光谱中持续存在(61),有些证据表明它一直存在于到N=35的振动光谱中(62)。
将光谱指派给单个异构体的困难在很大程度上是由于相关实验通常是探测非平衡系综的事实。即使在冷分子束中,也不能保证观察到的异构体实际上是最低能量的异构体,这是由于电子附着时显著的能量沉积以及可能存在的自动脱附通道,这些通道可能阻止了在计算搜索中发现的某些异构体的实验观察。(H2O)−6的复杂情况再次被说明,Jordan和同事(73, 74)使用单电子模型进行了 exhaustive sampling。一个代表各种局部最小值和连接它们的过渡结构的非连通性图在图4中显示,揭示了在全局最小值10 kJ/mol内的41个局部最小值!利用同位素替代的振动预解离实验揭示了在分子束中电子附着后最初形成的是(H2O)−6的书状异构体,而AA异构体随后形成(78)。可以找到一个连接这些异构体同时避免自动脱附的路径,但通过不少于13个中间局部最小值(74)。
从对(H2O)−6势能面的广泛视图中得出的重要教训是,尽管理论表明它们可能作为中间体短暂存在,但在振动预解离实验中并未观察到大多数低能异构体。这使得将理论与实验联系起来以阐明单个结构异构体变得极其困难,并暗示在比(H2O)−6更大的簇中,试图将实验光谱指派给单个簇异构体可能是愚蠢的。

图3 实验得到的振动光谱(底部)与缩放的DFT谐波频率计算得到的振动光谱(中间)。(a)O-D伸缩区域的光谱,其中插图显示了非常强烈的对称AA伸缩模式νs。(b)AA异构体在O-D弯曲区域的去卷积光谱。(c)“书”式异构体在O-D弯曲区域的去卷积光谱。在b和c面板中,还展示了以50%等概率轮廓的蓝色和绿色表示的单占据分子轨道。水分子根据其在水中氢键环境中的接受体或供体被标记为AA、AAD等。
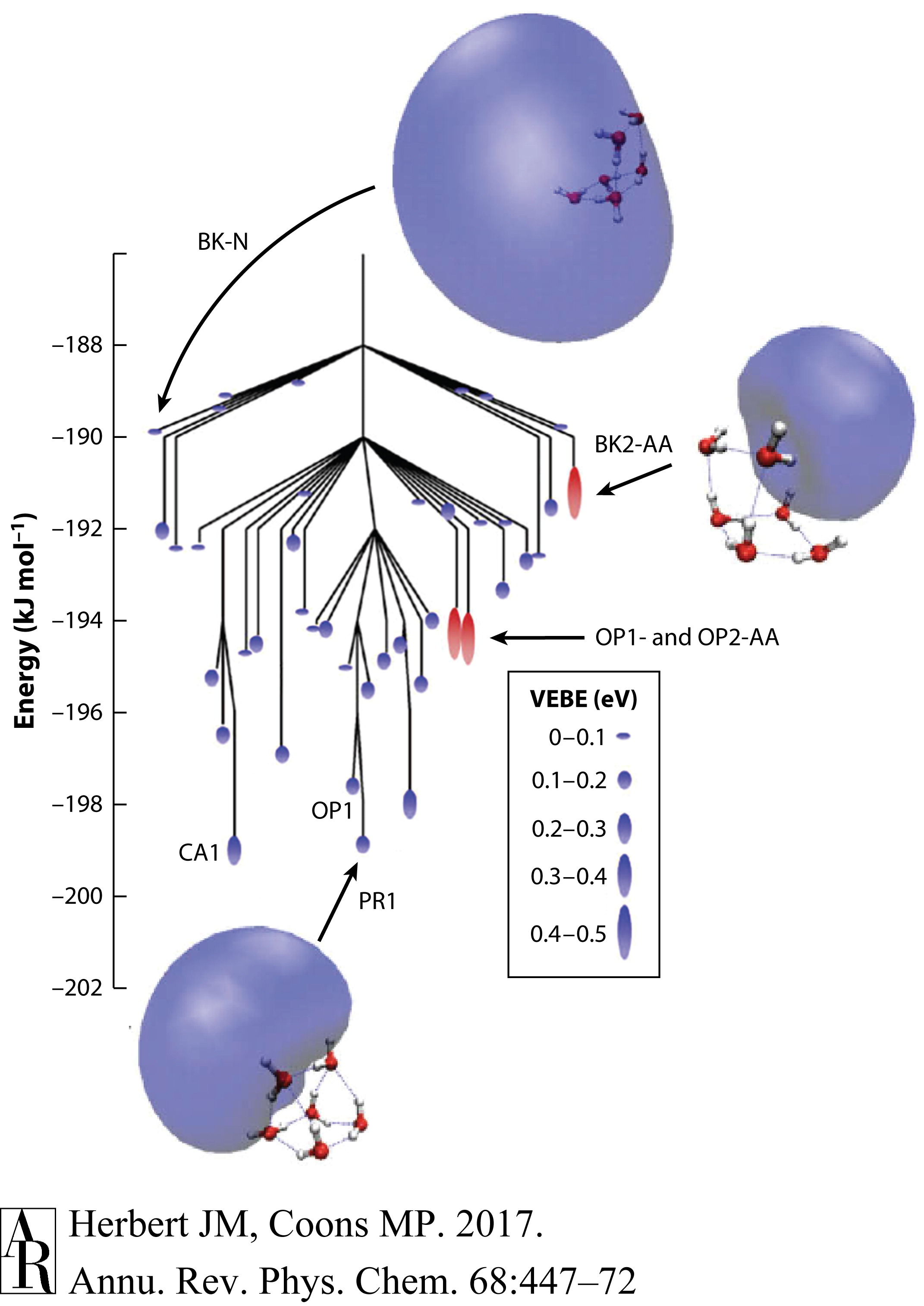
图4 (H2O)−6的断裂图的低能部分。分支的端点表示局部最小值,分支点表示连接它们的过渡态。一些最小值根据结构基元进行了标记:书式(BK),棱镜(PR),笼状(CA)或开放式棱镜(OP),其中明确指出了AA型异构体。对于每个局部最小值,彩色椭圆的大小表示VEBE的大小,AA型结构用红色标记,非AA异构体用蓝色标记。从分子束中最初形成的BK-N异构体开始,可以找到一条无自动脱离的路径通往也在实验中观察到的OP1-AA和OP2-AA异构体,但它通过了包括CA1、OP1和PR1最小值在内的总共13个中间局部最小值。
2.2. 更大的簇:表面状态与内部状态
在更大的簇中,随着簇大小的函数,电子从簇表面结合转变为可以合理地被视为体相水中水性电子有限类似物的过渡性质,这是一个持续的争论。Barnett等人(79, 80)的理论计算早在第一个实验光电子光谱之前就预测了在N=32–64的大小范围内表面结合和内部(空腔)结合簇异构体的存在。现代从头计算明确地证明了这两种类型的异构体都存在(81, 82);代表性的例子在图5中描绘。请注意,即使在内部结合的情况下,视觉检查也表明空腔中心的波函数尾部可能会穿透大约两个溶剂化层,并且使用空腔形成赝势模型模拟的水合电子表明氢键网络在前两个溶剂化层确实被破坏,但在第三层收敛到体相水的结构(83)。因此,即使是单电子模型也展示了在从头计算中注意到的大部分复杂结构,例如水分子之间的间隙中显著的电子密度(37)。
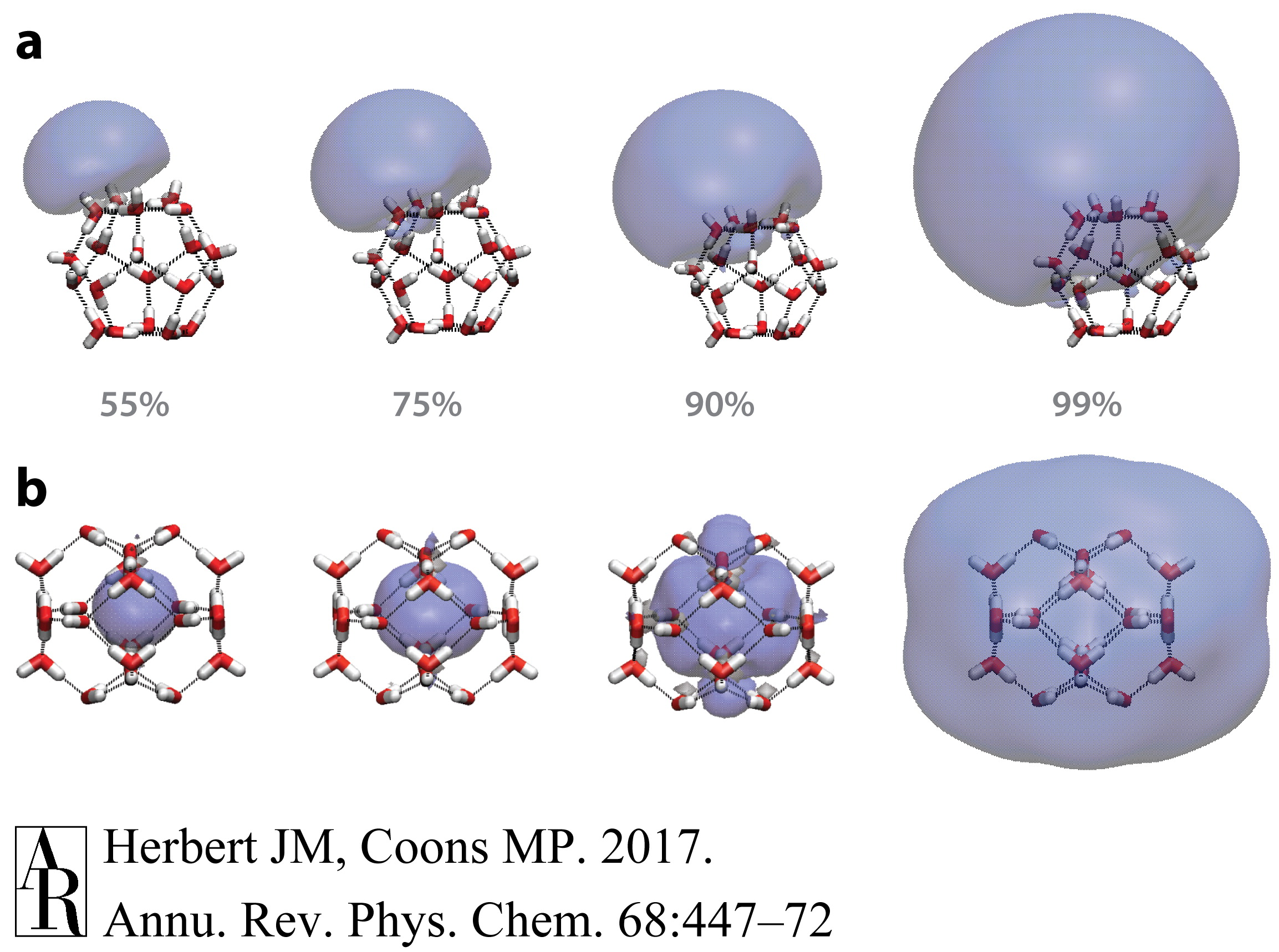
图5 在(a)表面结合异构体和(b)空腔结合异构体中的单占据分子轨道的等概率轮廓,每个异构体的VEBE都相似,约为1电子伏特。每个等值面包含所示的概率密度分数。
来自尺寸选择簇的光电子光谱的实验VEBEs(58–60)在图6中作为N−1/3的函数绘制。选择N−1/3是为了将簇数据与体相水中的水合电子联系起来,因为在一个简单的Born型溶剂化模型中,其中电子居住在一个固定大小的小球形空腔中,该空腔位于均质介电球的中心,半径为R,VEBE随R−1变化,对于大的球形簇,R∝N1/3。然而,后来的分析揭示了连续介质静电学也预测了表面结合电子的VEBEs随R−1变化(86),因此VEBEs的缩放行为在结合模式上是不明确的。

图6 对于尺寸选择的团簇的VEBE。(a)Neumark小组(59)通过光电子光谱测量的实验值,以及Johnson小组(70, 84, 85)主要使用红外预解离光谱测量的值。Neumark数据对于异构体I与Bowen小组(58)之前测量的值基本相同。Barnett等人(79)计算的理论值也显示为最初报告的值,以及根据文献59建议的特设因子0.6进行缩放的值。(b)Neumark小组(59)的数据(开放符号)与von Issendorff小组(60)在冷团簇中的更近期测量结果对比,后者将他们的两个数据系列标记为Ia和Ib,并将第三个系列(标记为vib)指定为光电子脱离时O-H拉伸的振动激发。
在这些实验中测量的光电子光谱显示出多个峰,这些峰被推测来自不同的异构体,其相对丰度对分子束的源条件敏感(59)。在图6a中标为I、II和III的数据系列是在对应于束温度TI>TII>TIII的条件下获得的(59)。所有三个数据系列大致随N−1/3变化,尽管在N=30–50范围内异构体II的数据改变了斜率。一个争议的来源是,假设代表内部溶剂化电子的异构体I数据与表面结合簇异构体的理论计算(44, 59)非常吻合,因为实验上没有观察到具有更大VEBEs的簇(87),而计算将内部溶剂化的簇放在更高的VEBEs(59)。然而,早期的单电子模型没有一个能定量预测VEBEs(83, 88),而Barnett等人计算的VEBEs经过特设缩放后,异构体I与预测的空腔结合异构体之间的一致性良好,而表面结合电子的VEBEs与异构体II一致(59)(见图6a)。
更近期的实验,其中簇在电子附着后在离子阱中冷却,揭示了新的数据系列“Ia”和“Ib”,它们似乎夹住了原始的异构体I数据(见图6b)。这些较新的数据表明,早期实验中温度特征不明显的,可能观察到了异构体Ia和Ib之间的转变。根据这些新数据,使用与高水平从头计算相比可定量预测VEBEs的赝势模型重新审视了簇问题(83)。在N=20–200范围内的簇阴离子模拟中定位了几类异构体(89)。这些在图7中以N=40的情况为例说明,包括偶极结合异构体(其VEBEs非常小,可以毫无争议地指定为异构体III);具有较大VEBEs的表面结合异构体;以及空腔型异构体。这些模拟中的新内容是区分了表面结合物种,其中电子是通过悬垂的O–H部分而不是简单地通过整体簇偶极矩结合的(如偶极结合情况),以及一个部分嵌入的异构体,其中簇表面的水分子已经重新定向自己,围绕未配对电子形成了部分溶剂化壳。
就像实验一样,模拟的簇系综对初始条件高度敏感,但尽管如此,它们与图6b中冷簇离子数据半定量一致(89)。模拟和测量的VEBE与N−1/3图的并列比较表明,异构体II是典型的表面结合物种,而最强结合的异构体Ib与空腔结合异构体的理论结果吻合得很好,当模拟簇被加热并允许退火时,一致性得到改善(89),就像提供图6b数据的离子阱实验一样。在异构体II和Ib之间是异构体Ia,模拟表明它可能是部分嵌入的物种(89)。

图7 四类团簇异构体的插图。在每种情况下,所示的等值线包含了未配对电子的|ψ|^2的70%。在偶极束缚异构体中,最多只有一个O-H组与电子形成氢键,结合主要来自整个团簇的偶极矩,导致电子相对弥散。表面结合异构体的特点是有几个O-H部分与电子形成氢键。在部分嵌入的情况下,额外的重定向形成了一个部分溶剂化层,使得电子仍然定位在团簇表面,但其紧凑程度类似于内部化的空腔结合物种。
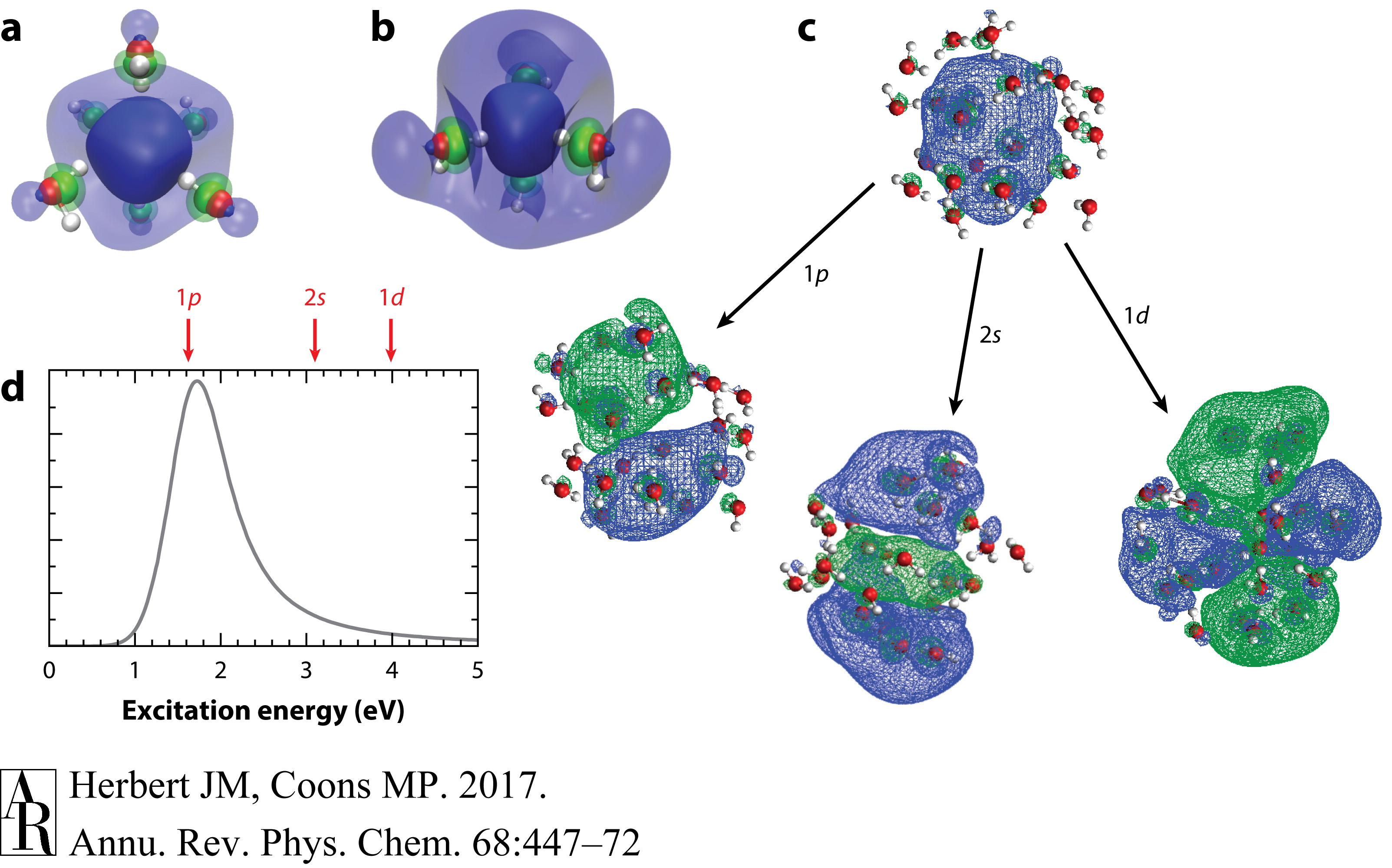
图8 (a) Kevan的(32)六配位模型用于水合电子和(b) Kumar等人的(92)四配位模型,两者都在这里描绘为在Hartree–Fock/6-31++G*水平上计算的单占据分子轨道,并带有电介质连续边界条件。半透明和不透明的等值面分别封装了40%和80%的概率密度,绿色(与蓝色相反的符号)表示电子波函数的尾部穿透到水分子的前沿轨道的地方。(c) 描述水合电子激发的自然过渡轨道。所示等值面在每种情况下封装了90%的概率密度。(d) 实验吸收光谱,指示了图c中所示特定快照的激发能级。
3. 水合电子(e−(aq))
由于问题涉及的是科学文献的总结和分析,而不是直接的数学或物理问题,所以这里将提供一个概括性的解答。
在液体水中水合电子的结构是一个持续讨论了数十年的话题。早期理论模型提出了一个球形空腔中的粒子假设(13, 26–29),而其现代从头算(ab initio)版本在描述水合电子的光谱学和热力学方面取得了显著的成功(90–92)。各种实验(32, 93)支持一个模型,该模型中几个水分子的O–H部分与水合电子的电荷分布(自旋密度)直接形成氢键,这一观点通过原子模拟得到了反复确认(33, 35–37, 83, 94)。Kevan基于低温碱性玻璃中的ESR测量提出的早期六配位模型(图8a)(32)最近让位于一个四配位图像(图8b)(83, 92, 94)。在这里,我们总结了理解水合电子的结构和动力学的努力,包括在体相液态水中以及在气/水界面上的情况。这个讨论是沿着用于研究这个物种的光谱技术组织的。
3.1 光电子光谱
对于水簇阴离子来说,光电子光谱可能是用来阐明结合模式的最不具侵入性的技术,正如第2节中的示例所证明的那样。然而,使用液体微喷光电子光谱测量体相水中水合电子的垂直电子束缚能(VEBE)的能力(96–101)作为对簇光电子光谱外推的重要检验。这些实验的共识是VEBE的范围在3.3–3.7 eV之间,大多数值在3.3–3.4 eV范围内(101),这与簇外推(102)以及使用包含自洽电子-水和水-水极化的赝势模型的模拟结果完全一致(83)。
然而,在一个特定的微喷实验中,观察到1.6 eV的特征,其寿命≥100 ps,被归因于在水/真空界面处结合的水合电子(99)。尽管这个值与在非晶固态水表面测得的1.4 eV VEBE(103)以及簇光电子数据针对异构体II的外推相似(图6a),但其他人试图在液/气界面复制这一结果时只发现了一个短暂的特征,其寿命约为∼100 fs(98, 100)。这包括在低电子动能下进行的实验,其中电子的衰减长度相对较短(104),因此光谱应该由界面处结合物种的信号主导(100)。给定一个s→p激发能量为1.7 eV和体相VEBE为3.3–3.4 eV,一个短暂的特征具有1.6 eV的VEBE与水合电子的瞬态激发态一致,或者可能是有时被称为预溶剂化电子的前驱体(47, 55)。然而,这并没有解释在99中观察到的具有约100 ps寿命的更长寿命信号。这与测量的内部转换寿命60–75 fs不一致(105, 106)。尽管如此,有人提出假设,即在真空能级下方1.6 eV处的假定界面电子可能在DNA的辐射化学中起作用,具体来说,界面处较低的VEBE可能为DNA的解离电子附着提供了适当的能量,导致单链断裂(99, 107–110)。这一假设要求界面物种的能量≤真空能级下方2.5 eV(107, 108),这与模拟数据不一致,暗示界面处的VEBE与体相值相当(111)。此外,模拟表明当电子被引入平衡后的气/水界面时,电子在约30 ps内溶解到体相溶液中(111),如图9所示,界面处最多只有一个浅的自由能最小值(112)。
根据模拟结果,电子在界面引入后约∼10 ps内就得到了足够的溶剂化,以至于它的VEBE(垂直电子结合能)与预测的体相水中水合电子的VEBE非常相似。从头计算包括超过80个量子力学水分子,预测界面的VEBE为3.1–3.2 eV,而体相物种的VEBE为3.4–3.5 eV(111)。这表明,不仅液体微喷光电子光谱可能无法区分体相与界面信号,更重要的是,两种物种似乎都不具备诱导DNA解离性电子附着的适当能量(111)。
在冰面上的情况则大不相同。Wolf及其同事在非晶态固体水上的实验(103, 113, 114)支持一种与图9中t=0快照不完全相同的观点,即概率密度的“气球”弱锚定在表面,可能占据一个Bjerrum缺陷(113)。当在冰面上沉积一层Xe原子时,这个假定的界面电子的信号被猝灭(103, 113, 114),支持了一种结合模式的概念,即电子显著超出界面。在非晶态固体水表面上,水合电子的信号在分钟时间尺度上持续存在(113),并且可以在氯氟烃中诱导解离性电子附着(114)。这可能表明水合电子在冰粒子上发生的大气化学中起作用(115–117),其中电子是由宇宙射线产生的,尽管这一说法仍有争议(118, 119)。
图9 水合电子从气/水界面演化到体相溶液中。在t=0时,电子局限在由界面上的悬空O-H部分产生的表面陷阱中,但在约10皮秒内,它形成了一个从光谱上讲与体相水中的水合电子基本无法区分的物种,并在约30皮秒内溶解进入体相溶液。不透明和半透明的等值面分别封装了50%和95%的概率密度。标注描绘了基于参考文献91中报告的计算的相关DFT自然过渡轨道,与最低的s→p激发相关。
3.2 振动光谱学
与簇合物一样,振动光谱学通常比光电子光谱学更能深入探测结构,而在同位素替代水中的水合电子的共振拉曼光谱提供了重要的结构信息。对于溶解在H2O或D2O中的水合电子,水的弯曲区域由一个单一峰组成,但在H2O和D2O的混合物中,这个峰以暗示每个H2O分子只有一个O–H部分与电子配位的方式分裂(93)。这与从大多数水合电子的原子模拟中获得的结构模型一致,例如图8中的那些,但与偶极向量朝向电子的模型不一致。这似乎也与电子在一个或多个水分子上离域的模型不一致(38, 120, 121)。
使用表面敏感振动光谱学检查了空气/水界面上的水合电子(122, 123)。一组实验在有和没有一层表面活性剂分子的情况下进行,其思想是它们的存在于是会破坏任何显著超出界面的结构的界面绑定电子,如图9中t=0快照中所示。然而,当表面活性剂的极性部分较小时(如癸醇的羟基部分),与无表面活性剂界面相比,观察不到光谱变化,但当极性团较大时信号显著改变(122)。作者得出结论,假定的界面水合电子可能位于溶剂中1–2 nm处(122),足够靠近界面以消除反演对称性从而提供信号,但根据如图9所示的模拟,它距离足够远,其结构非常类似于体相水中的水合电子。与冰不同,在那里归因于界面电子的信号在分钟时间尺度上持续存在,这些实验表明界面信号存活约≈750 ps(122)或可能≲100 ps(123)。
3.3 光学光谱学
水合电子的最显著特征是其电子吸收光谱,这是监测此物种的主要手段。该光谱绘制在图8d中,并在各种热力学条件下进行了实验表征(124)。它在红边呈现高斯线形,在蓝边呈现洛伦兹线形(102),这些特征也在簇合物的电子光谱中显而易见(125)。人们对于这一光谱中的“蓝尾”给予了极大的关注,因为在大多数理论计算中并未再现这一特征(126)。鉴于洛伦兹线形(暗示寿命展宽),以及吸收光谱的蓝边与光电子光谱的红边重叠的事实(127, 128),这一尾部长期被归因于束缚→连续态转换(27, 127, 129)。然而,这并没有完全解释理论计算中缺少尾部的原因,许多这样的计算使用实空间网格并原则上能够描述连续态。相比之下,使用包含自洽电子-水极化的一个电子模型的计算确实再现了蓝尾(83, 95),这些计算表明尾部中至少一些状态是高度离域的,准连续波函数,但仍然是束缚态,因为激发态能量低于真空水平(95, 130)。在这些计算中,水分子的极化响应在放大问题状态的振子强度方面发挥了关键作用。鉴于测量到的水合电子吸收光谱的积分振子强度值为1.14(131),这一点很有趣。>1的值意味着水合电子的激发不是严格的一个电子跃迁,而是一些强度是从水分子上的电子借用的。
本段描述了电子在水溶液中的光学光谱可以通过粒子在盒子模型中的行为来解释。时变密度泛函理论(TDDFT)自然转换轨道,显示在图8c中,通过原子模拟计算得出,可以容易地被赋予粒子在腔量子数。最低的三个激发类似于允许的1s→1p跃迁,这三个跃迁基本上定量地解释了光学光谱的主要高斯部分,如图10a所示。由于原子模拟中的腔是椭圆形和流动的,1s→1p跃迁是不均匀展宽的,这解释了光谱的宽度。对于严格球形腔,1s→2s激发是禁止的,这解释了主要1s→1p带之外强度的急剧下降。然而,更高能级的跃迁进入2s、1d和准连续轨道从1s→1p激发借用强度,因此要与整个光谱范围的实验结果一致,需要计算的不仅仅是最低的三个状态(42, 83, 91, 95)。如图10a所示,最低的15个TDDFT激发态就足够了。
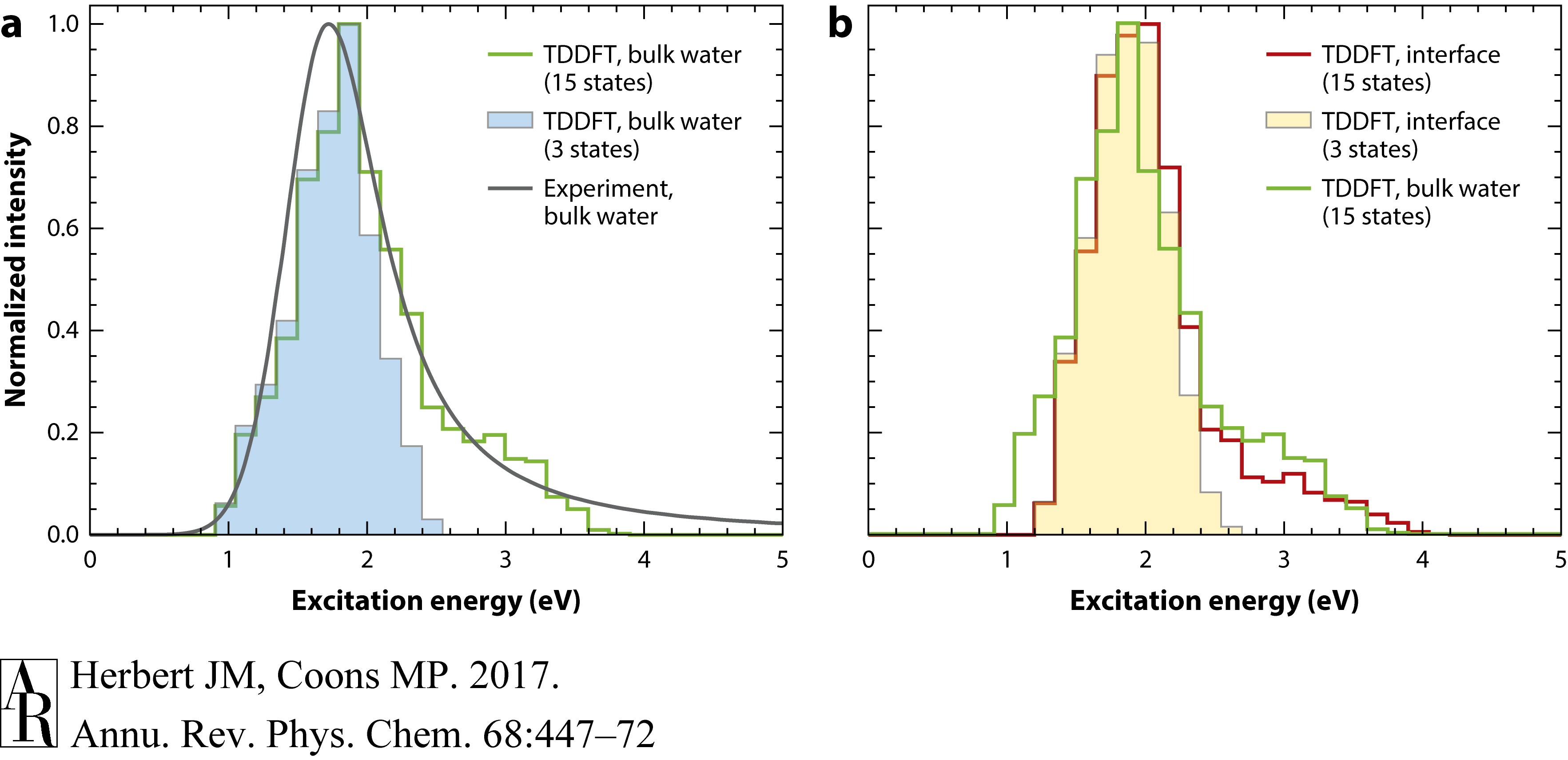
图10 (a) 体相水中水合电子的光吸收光谱,实验光谱与TDDFT计算结果叠加;(b) 在水/真空界面处,只有TDDFT结果可用。在面板b中,计算得到的界面光谱与在同一理论水平上计算的体相光谱叠加,以供比较。显示了两种不同的理论计算:一种使用最低的3个激发态,另一种使用15个激发态,每种情况下都按振子强度加权,并使用参考文献91的数据。所有光谱在其各自的吸收最大值处归一化为单位强度,但计算中没有使用拟合。缩写:TDDFT,时间依赖密度泛函理论。
可解析解模型预测,VEBE和1s→1p的激发能完全由电子的旋转半径决定,
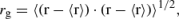 2
2
特别地,这些关系式以r-2g 的形式变化。这种r-2g依赖性在水合电子在体相水中的凝聚相模拟中自然出现(33, 37),但在簇数据中更为明显;见图11a。簇的VEBE和电子吸收最大值紧密遵循由粒子在腔模型预测的rg 曲线,这对于内部溶剂化的电子是合适的,并且对于一个更合理的表面结合电子的单电子原子模型也是如此(89)。重要的是,与体相模拟相比,簇样本覆盖了更广rg 值范围,因此这些关系在广泛的模拟数据(89, 90)中的稳健性表明,仅知道rg 就足以对VEBE和吸收最大值进行半定量预测。
这种关系解释了例如,当水合电子在空气/水界面变得溶剂化时,VEBE的迅速增长(图9),因为即使在界面形成部分溶剂化壳也足以将电子定域到其半径与体相物种没有多大差异的程度(111)。这也可以很容易地从簇数据中看出,特别是在图11b中显示的图表中,当电子质心距离簇表面>5 Å时,rg 收敛于>3.5 Å的值,当质心到达界面时,rg 接近体相值(rg =2.45$ Å)。
鉴于rg 在界面的迅速收敛,以及这一属性本身就提供了对光学吸收最大值的良好猜测,人们可能会预测,在空气/水界面处的水合电子的光学光谱与体相水中的水合电子不会有太大的不同。界面光谱尚未测量,但可以进行模拟,结果如图10b所示,与相应的体相水计算重叠。两个光谱在大多数地方只有微小的差异,吸收最大值是相同的。因此,无论是在光电子还是电子吸收光谱方面,体相水中的水合电子与空气/水界面处的水合电子似乎没有多大区别。
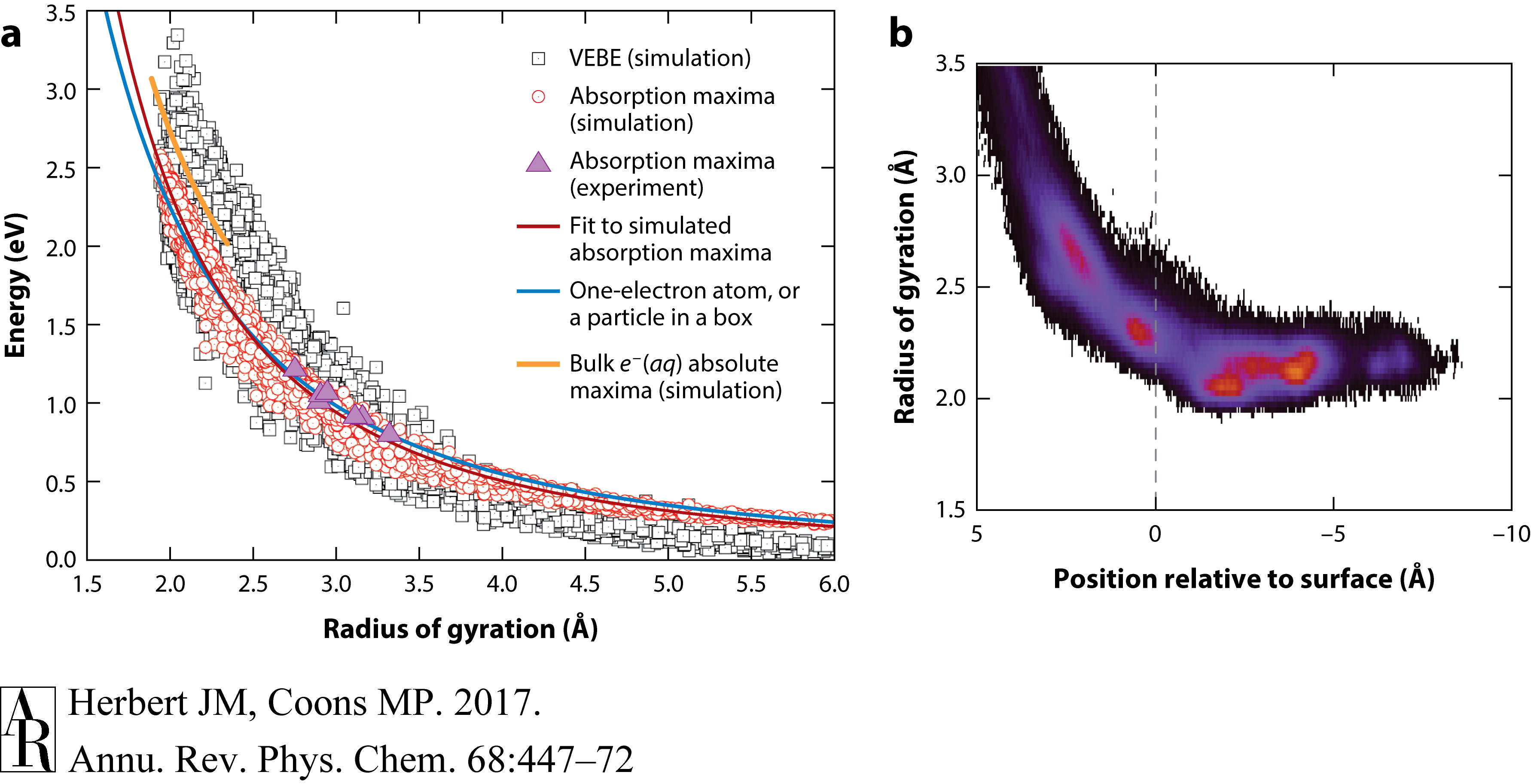
图11 (a) 电子的回转半径rg与其VEBE(灰色方块)和电子吸收最大值Emax(红色圆圈)之间的相关性,根据N=20–200在不同条件下的模拟数据获得。团簇中Emax的实验结果也显示出来(紫色三角形),以及体相水中水合电子的Emax的模拟结果(橙色曲线)。蓝色曲线表示一个电子原子的最低激发能量随rg的变化,其形式与球形腔中粒子的类似结果几乎相同(89)。(b) 显示rg如何随着电子质心与团簇表面之间的距离收敛的直方图,负值表示内部化的电子。
4. 理论模型
4.1.规范腔模型
上述讨论中隐含了一个假设,即电子占据了液体水结构中的排除体积,在某些版本的腔模型中。而Kevan(32)在1981年基于ESR实验提出了一个六配位模型(图8a),并且在T=77 K的碱性玻璃状水中,进一步指出配位数小于或等于4与ESR线型不一致(132),现代DFT(37)和赝势模拟(83, 94)在T=300 K的纯净水中展示了略大于4的配位数(图8b)。这些模拟(35, 36, 83, 133)在约∼1 ps内自发形成腔。应该记住,在室温下腔是非常流动的,通过水分子的摆动运动塌陷并重新形成(83, 134),这与水合电子的非常快的扩散一致。在水溶液离子中,水合电子的扩散比H+(aq)的Grotthuß辅助扩散稍慢,但与OH−(aq)相当,其Grotthuß型扩散也受到摆动运动的辅助(135)。基于离子迁移率测量(136),水合电子的扩散速度是K+(aq)的三倍。水在空气/水界面的摆动运动与体相水中相似(137),与水合电子在界面的短寿命一致。
腔模型定量地再现了大量实验数据。这些包括溶剂化自由能(92),或者换句话说,液态水的绝热电子亲和能;VEBE(83, 111);以及电子吸收光谱(83, 91, 95),包括蓝色尾部和线宽,后者可以转换为回转半径(rg=2.45 Å),这也与模拟数据(83)和DFT计算(92)一致。模拟还展示了第一溶剂化壳中的摆动动力学和氢键结构,与从共振拉曼光谱推断的结果一致(83),即每个水分子有一个O–H e−氢键,且H2O摆动的恢复力减弱(93)。DFT计算再现了直接与电子配位的O–H键伸缩频率的约200 cm−1红移(92)。对于扩散系数(83, 134)获得了半定量结果,包括其温度依赖性(134)。最后,对四配位腔型模型结构的DFT计算得到了相对于自由电子值的电子g因子移动的半定量值(92)和ESR超精细耦合常数(92, 138)。如果底层水模型是可极化的(130),则这些特征大多数可以通过单电子模型再现(83),尽管振动频率移动、g张量移动和超精细耦合常数需要水分子上的轨道,因此需要多电子处理来描述这些属性。
绝大多数理论结果和与实验的比较都与中心在腔的自旋密度一致,但其尾部显著延伸到溶剂中。这已经在簇中很明显(图5),计算表明只有40-50%的自旋密度包含在腔本身内(37, 82)。氢键结构和动力学的破坏延伸到第二溶剂化壳,但没有延伸到第三溶剂化壳(83)。尽管有这样有利的一致性,但多年来也提出了其他结构性模型,如下所述。
4.2. 溶剂阴离子模型
1991年,Tuttle和Golden重新审视了电子和碘离子在各种溶剂中的电子光谱(139),发现碘离子光谱对温度和溶剂都不敏感,而电子的光谱对两者都很敏感。这一观察结果使得之前的提议(120, 121)重新受到关注,即所谓的溶剂化电子可能更适合被概念化为分子阴离子。
碱金属的电子亲和性表明它们的阴离子M−在气相中是稳定的(140),而极性溶剂(S)应该进一步稳定这些阴离子。推测的模型(120)由金属和溶剂阴离子之间的平衡以及离子配对过程和组成。溶剂阴离子S−被提出存在于代替腔束缚的溶剂化电子的位置。对这些平衡的连续体处理与金属-氨溶液中蒸汽压、电导率和NMR Knight位移(14N)的温度依赖性的实验结果定性一致(120),尽管目前尚不清楚现代对腔模型的理解是否与溶剂核的Knight位移不相容。
导致Tuttle和Golden支持溶剂-阴离子复合物模型的一个主要因素似乎是1980年代的电子-水伪势无法正确描述水合电子吸收光谱的位置和形状,尽管新的模型现在不需要拟合就能再现峰值位置(83, 94)。作为进一步的证据,Tuttle和Golden(121, 139)引用了溶剂-阴离子模型解释了溶剂化电子的光学光谱在二元溶剂混合物中的轻微组成依赖性,通过一个由两种溶剂中的溶剂阴离子之间的平衡组成的双吸收体模型:S−1+S2⇇S1+S−2。尚未有人尝试模拟混合溶剂中的溶剂化电子,因此没有理由假设腔型模型必然限于单吸收体模型,因为不同的局部溶剂化环境可能很容易产生略有不同的吸收光谱。尽管用现代从头算模拟的定量工具来追求这一点将会很有趣,尽管Tuttle和Golden认为“没有令人信服的理由赋予溶剂化电子腔型的...构造”(139, p. 5735),鉴于现代理论如何成功地基于腔模型解释水合电子的性质,我们得出结论,目前没有令人信服的理由去考虑溶剂-阴离子模型。
4.3. 水合氢化铵模型
罗宾逊和同事们(136)提倡了一个与溶剂-阴离子模型略有不同的版本,其中负责归因于水合电子的光谱特征的物种实际上是和HO−的复合物。这一假设最近被Domcke 和 Sobolewski(108, 141)重新提出,他们提出了一个略有不同的模型,其中H3O(aq)在水合时形成一个两性离子复合物H3O+…e−,这种行为在团簇的单占据轨道中是显而易见的(图12)。加入三个水分子后,一个3s Rydberg型轨道从H3O核心脱离,留下一个作为氢键网络一部分的水合氢离子。最低激发能量(Rydberg)在微水合时从2.2 eV急剧转移到1.5 eV,而H3O的简并2E(pxy)态的分裂导致了D0→2E(pxy)和D0→2A(pz)跃迁,这些跃迁覆盖了1.1–3.0 eV的范围,并且总振子强度接近于1(141),这与归因于水合电子的光学光谱一致。
振动频率(141)和共振拉曼强度(142)已经使用DFT为团簇计算出来,并且对于直接配位到单占据轨道的O-H部分显示出特别强烈的O-H伸缩振动。这与解释这些振动在团簇中增强强度的电荷摇摆机制一致(77)。模拟的共振拉曼光谱与测量的水合电子的共振拉曼光谱定性一致(93)。尽管这些计算没有扩展到比更大的团簇,但是电子电荷与溶剂分子分离,并且似乎与每个水分子的一个O-H部分形成氢键的事实表明,水合电子的水合氢离子模型可能与腔模型并没有太大的不同。
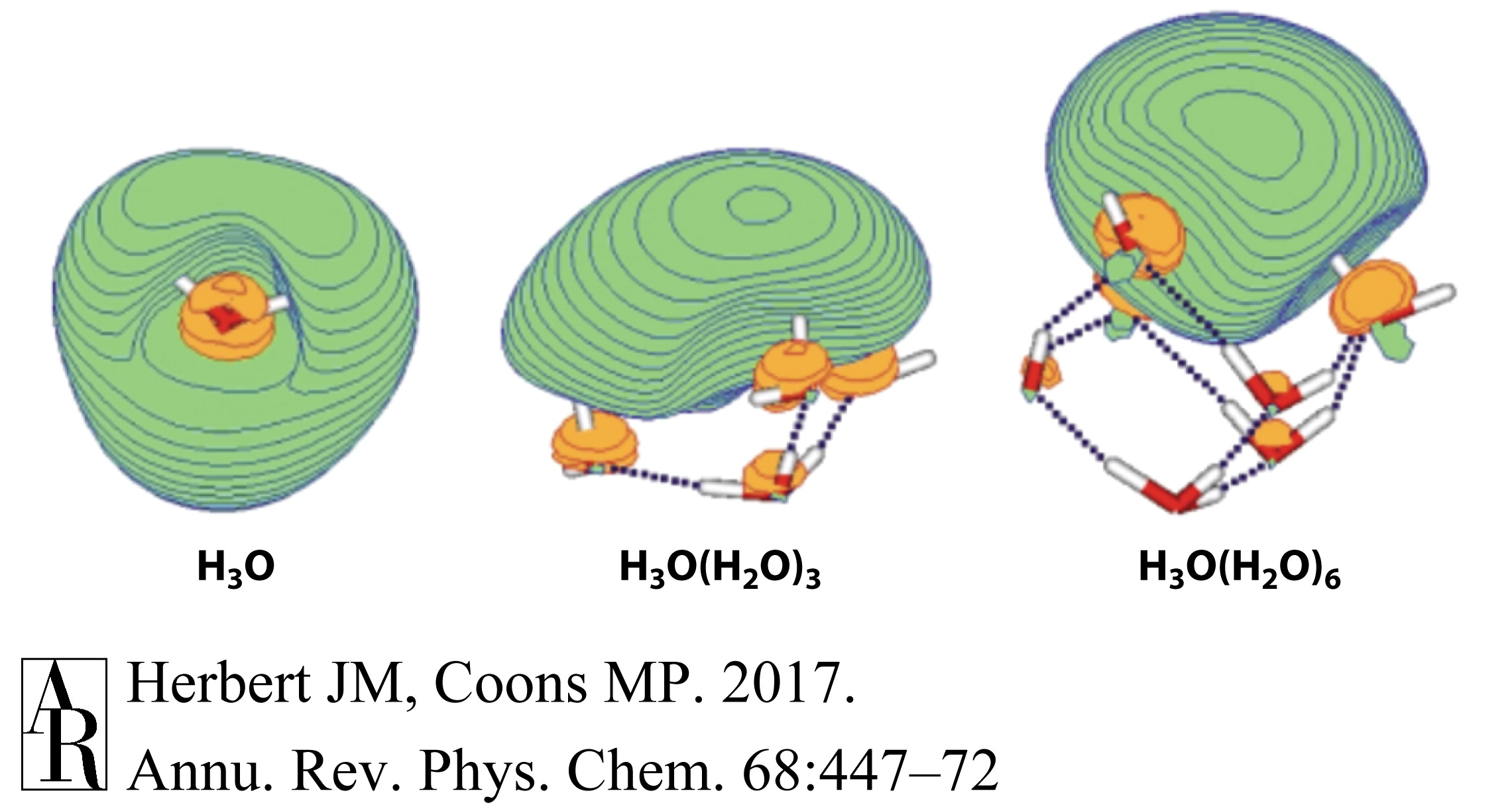
图12 水合氢离子团簇的单占据分子轨道。
4.4. 非腔模型
2010年,Larsen, Glover和 Schwartz (LGS)报告了一个电子-水伪势模型,该模型在吸引和排斥相互作用之间提供了质的不同平衡,并预测了一个根本不涉及排除体积的水合电子结构(38)。相反,水分子渗透到未配对电子的波函数中,使得水密度在电子中心附近最大(ρ=1.23 g/cm³)。尽管如此,这个模型的波函数的回转半径(rg=2.6 Å)接近实验值(2.45 Å),并且由于过剩电子波函数的大小已被证明是决定其激发能量的关键因素(89),因此LGS模型再现吸收光谱的主要特征并不令人惊讶。
非腔LGS模型仍然存在争议(39-42)。在未配对电子区域增强的水密度很难与测量的水合电子的部分摩尔体积在校正电致收缩效应后为正值的事实相调和(30, 143),这一事实有时在文献中被误引用,如42所讨论的。最近的这种测量与腔体半径≈2.2 Å一致(31)。此外,LGS波函数对于团簇在定性上与从头算结果不一致(40)。LGS模型源自应用于的精确伪势理论,就像其他两个形成腔体的模型一样(83, 94),
转载本文请联系原作者获取授权,同时请注明本文来自孙学军科学网博客。
链接地址:https://wap.sciencenet.cn/blog-41174-1422130.html?mobile=1
收藏

