智能不是数学，但数学一定是智能

三次数学革命深刻地塑造了智能的发展，并且在“连续”与“离散”、“代数”与“几何”、“有限”与“无限”以及理性与感性之间架起了桥梁。第一次数学革命（无理数的发现）揭示了数轴的连续性，打破了离散的有理数体系，推动了代数从几何中独立出来，引发了对无限的初步探索，并促使人类从感性认知向理性思维转变。第二次数学革命（微积分的创立）通过极限和无穷小的概念，将离散的差分与求和转化为连续的导数与积分，将代数与几何紧密结合，系统地处理了无限的概念，极大地增强了人类智能在处理动态和连续变化问题上的能力。第三次数学革命（康托集合论的诞生）则进一步深化了对无限的理解，区分了可数与不可数集合，为离散与连续的关系提供了更清晰的框架，推动了数学的逻辑化和形式化，为智能的逻辑推理和形式化方法奠定了基础。这三次革命不仅推动了数学的理性化，也促进了人类智能的发展，使得智能能够更系统地处理连续与离散、代数与几何、有限与无限的关系，从而在理性与感性之间找到了平衡。

一、数学的三次革命

数学的三次革命（通常指无理数的发现、微积分的创立和康托集合论的诞生）深刻地改变了数学的面貌和思维方式，同时也与“连续”与“离散”、“代数”与“几何”、“有限”与“无限”以及理性与感性等概念有着密切的关系。

1. 第一次数学革命：无理数的发现

古希腊数学家在研究几何问题时，发现了无理数（如√2）。这一发现打破了当时数学家对“数”的认知，因为在此之前，他们认为所有数都可以表示为两个整数的比（即有理数）。

(1)与“离散”与“连续”的关系

有理数是离散的，因为它们可以被一一列举出来。无理数的发现揭示了数轴是连续的，因为无理数填补了有理数之间的“空隙”。这一发现使得数学家开始意识到连续性和离散性之间的差异。

(2)与“代数”与“几何”的关系

无理数的发现源于几何问题（如正方形对角线的长度问题），但其解决却推动了代数的发展。代数开始从几何中独立出来，成为研究数的性质和运算的独立学科。

(3)与“有限”与“无限”的关系

无理数的发现引发了对无限的思考。例如，无理数的小数表示是无限不循环的，这使得数学家开始研究无限的概念，为后来的极限理论奠定了基础。

(4)与理性与感性的关系

无理数的发现是一个理性的突破，它挑战了古希腊数学家的直觉和感性认知。这一发现推动了数学的理性化，强调了逻辑和证明的重要性。

2. 第二次数学革命：微积分的创立

微积分的创立解决了运动和变化的问题，是数学史上的一次重大突破。

(1)与“离散”与“连续”的关系

微积分的核心是极限理论，它处理的是连续变化的量。微积分通过极限的概念，将离散的差分和求和转化为连续的导数和积分，从而能够处理连续的运动和变化。

(2)与“代数”与“几何”的关系

微积分将代数和几何紧密结合。通过坐标系，几何问题可以用代数方法解决，代数问题也可以通过几何直观来理解。例如，导数可以看作是曲线的切线斜率，积分可以看作是曲线下的面积。

(3)与“有限”与“无限”的关系

微积分的核心是极限和无穷小的概念。它通过无限逼近的方法，将有限的差分和求和转化为无限的过程，从而解决了连续变化的问题。这一理论的创立使得数学家能够处理无限的概念，并将其应用于实际问题。

(4)与理性与感性的关系

微积分的创立是理性思维的胜利。它通过严格的逻辑和数学工具，解决了运动和变化的问题，这是感性认知所无法达到的。微积分的创立推动了科学的理性化，为现代科学的发展奠定了基础。

3. 第三次数学革命：康托集合论的诞生

康托的集合论引入了无穷集合和超穷数的概念，为数学的逻辑基础和无限理论提供了新的视角。

(1)与“离散”与“连续”的关系

集合论将离散和连续统一起来。康托通过集合的概念，定义了可数集合和不可数集合，从而揭示了离散和连续的本质区别。例如，自然数集合是可数的，而实数集合是不可数的。

(2)与“代数”与“几何”的关系

集合论为代数和几何提供了统一的框架。通过集合的概念，数学家可以将代数结构和几何结构统一起来，从而更深入地研究数学的本质。

(3)与“有限”与“无限”的关系

集合论的核心是无限集合的研究。康托引入了超穷数的概念，区分了不同层次的无限，从而解决了无限的悖论和矛盾。这一理论使得数学家能够更系统地研究无限的概念。

(4)与理性与感性的关系

集合论的创立是对理性思维的极致追求。它通过严格的逻辑和定义，解决了无限的悖论和矛盾，推动了数学的逻辑化和形式化。集合论的创立也引发了对数学基础的重新思考，进一步强化了数学的理性化。概括起来，三次数学革命分别从不同的角度推动了数学的发展，同时也深刻地影响了“连续”与“离散”、“代数”与“几何”、“有限”与“无限”以及理性与感性的关系。这些革命不仅扩展了数学的边界，也深化了我们对数学本质的理解，推动了数学的理性化和形式化。

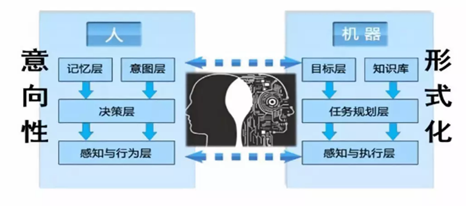
二、三次数学革命与智能的关系

三次数学革命不仅是数学自身发展的里程碑，也对智能（包括人类智能和人工智能）的理论基础和实践应用产生了深远的影响。

1. 第一次数学革命：无理数的发现

（1）对人类智能的影响

实现了逻辑思维的提升，无理数的发现迫使古希腊数学家重新审视数的概念，推动了逻辑思维和证明方法的发展，这种对基础概念的质疑和重新定义，培养了人类对复杂问题的理性分析能力。进一步深化了抽象思维，无理数的发现揭示了数轴的连续性，这需要人类具备更高的抽象思维能力来理解无限和连续的概念，这种抽象思维能力是人类智能的重要组成部分，也为后来的数学和科学理论奠定了基础。

（2）对人工智能的影响

为算法设计打下了基础，无理数的存在使得计算机算法在处理数值计算时需要考虑浮点数的精度问题，如计算机科学中的浮点数表示和误差分析，都与无理数的性质密切相关。加大了模型的复杂性，无理数的发现提醒人工智能研究者，模型需要能够处理连续的输入和输出，在机器学习中，连续的特征值和目标值需要通过合适的数学工具（如微积分）来处理。

2. 第二次数学革命：微积分的创立

（1）对人类智能的影响

提升了处理动态问题的能力，微积分的创立使得人类能够处理动态和变化的问题，如运动物体的速度和加速度、曲线的切线和面积等，对动态系统的分析能力是人类智能的重要体现，也为物理学、工程学等领域的研究提供了强大的工具。同时也增强了数学建模的能力，微积分的创立推动了数学建模的发展，使得人类能够通过数学公式来描述和预测复杂的自然现象，这种建模能力是人类智能的重要组成部分，也是现代科学研究的核心。

（2）对人工智能的影响

优化了算法的基础，微积分中的导数和梯度概念是优化算法的核心，在机器学习中，梯度下降算法用于优化模型参数，其理论基础正是微积分中的导数和梯度。实现了连续系统的建模，微积分使得人工智能能够处理连续的输入和输出，如在深度学习中，神经网络的激活函数和损失函数通常是连续的，微积分提供了计算这些函数导数的工具，从而实现模型的训练和优化。

3. 第三次数学革命：康托集合论的诞生

（1）对人类智能的影响

深化了对无限的理解，集合论的创立使得人类能够系统地研究无限的概念，包括可数无限和不可数无限。这种对无限的理解是人类智能的高级体现，也为数学和逻辑学的发展提供了新的视角。推动了逻辑和形式化的发展，集合论的创立推动了数学的逻辑化和形式化，使得人类能够更严格地定义和处理数学概念，这种逻辑和形式化的思维方式是人类智能的重要组成部分，也为计算机科学和人工智能的发展奠定了基础。

（2）对人工智能的影响

升华了数据结构和算法的基础，集合论为计算机科学中的数据结构和算法提供了理论基础，集合、映射、关系等概念在数据库、图论和算法设计中广泛应用。拓展了逻辑推理和形式化方法，集合论的逻辑化和形式化方法为人工智能中的逻辑推理和形式化方法提供了工具，在知识表示和推理中，集合论的概念被用来定义知识库和推理规则。

总之，三次数学革命分别从不同的角度推动了人类智能的发展，并为人工智能的理论基础和实践应用提供了重要的支持。第一次数学革命提升了人类的逻辑和抽象思维能力，为计算机算法的精度和复杂性处理提供了基础；第二次数学革命增强了人类处理动态和连续系统的能力，为人工智能中的优化算法和连续系统建模提供了工具；第三次数学革命深化了人类对无限和逻辑的理解，为人工智能中的数据结构、算法设计和形式化方法提供了理论支持。这些数学革命不仅推动了数学自身的发展，也为智能科学的进步提供了强大的动力。