科学网-一类多生产线可重入制造系统的层次化鲁棒控制策略-苗焕玲的博文

一类多生产线可重入制造系统的层次化鲁棒控制策略

2025-5-23 08:45

阅读：182

论文简介

【编辑荐语】

本文将给大家分享《控制理论与应用》第41卷第12期论文"一类多生产线可重入制造系统的层次化鲁棒控制策略(A hierarchial robust control strategy for multi-line re-entrant manufacturing systems)". 如您对本文相关内容有好的理解与建议, 欢迎评论区留言.

本文针对多生产线可重入制造系统的复杂动态特性, 提出了一种层次化智能控制策略. 该策略融合双曲型偏微分方程建模、T-S模糊逻辑与滑模控制技术, 构建了兼具实时响应与强鲁棒性的分层控制架构. 通过引入非线性控制通道和生产场景耦合机制, 系统能够快速适应市场需求波动并抑制多源扰动, 其核心突破在于将控制器参数设计转化为凸优化问题, 利用多项式时间算法进行高效求解, 解决了传统滑模控制在连续时间PDE模型中的维度限制. 理论层面, 本文基于李雅普诺夫稳定性分析证明了闭环系统的有限时间指数收敛特性, 并通过仿真验证了该方法在提升设备稳定性(故障率降低40%)和运行效率(提升35%)方面的显著效果. 该研究为高维非线性制造系统提供了可扩展的智能控制范式, 其多学科交叉思路对柔性制造和智能工厂优化具有重要参考价值.

【论文介绍】

一类多生产线可重入制造系统的层次化鲁棒控制策略

A hierarchial robust control strategy for multi-line re-entrant manufacturing systems

张春阳1,2, 高庆1,2, 吕金虎1,2, 陈巍3,2,4,5,6, 王健男3,2,5,6

单位机构: 1. 北京航空航天大学自动化科学与电气工程学院; 2. 中关村实验室; 3. 北京航空航天大学人工智能研究院; 4. 北京航空航天大学数学科学学院; 5. 北京航空航天大学数学信息与行为教育部重点实验室; 6. 鹏城实验室

引用: 张春阳, 高庆, 吕金虎, 等. 一类多生产线可重入制造系统的层次化鲁棒控制策略. 控制理论与应用, 2024, 41(12): 2237 – 2248.

DOI编号: 10.7641/CTA.2023.20401

全文链接: https://jcta.ijournals.cn/cta_cn/ch/reader/view_abstract.aspx?file_no=CCTA220401&flag=1

摘要

本文针对一类多生产线的可重入制造系统提出了一种层次化智能控制策略. 基于层次化建模的技术, 本文提出双曲型偏微分方程用以描述系统动态, 并且设计了对应的鲁棒控制器用来实现制造系统在有限时间内平稳运行的目标. 该控制策略结合T-S模糊建模技术和滑模控制策略, 在H∞指标下实现了闭环制造系统抑制系统中广泛存在的扰动. 由于所提出的控制器具有无穷维的特点, 本文提出了一种基于凸优化技术的数值计算方法用来高效求解控制器参数. 最后, 给出的仿真算例验证了该控制策略的有效性和优点.

引言

可重入制造系统是一个涵盖了产品制造全过程以及全生命周期的动态输入输出系统, 输入为毛坯、原材料、能源和信息等资源, 输出为零部件、半成品或产品. 毛坯到达、加工开始、设备故障、加工完成等均是引起系统状态改变的事件. 因此, 可重入制造系统是一类复杂的离散事件系统. 为描述制造系统中的离散事件引起的状态变化, 常用的数学模型包括Petri网模型和排队网络模型. Petri网模型适用于描述并行事件和并行运行的生产线; 排队网络则将每条流水线看作一条单独的离散队列, 通过排队网络将不同队列连接, 可以非常方便地描述生产流. 但是, 当处理以半导体加工为代表的具有大规模制造资源、海量机器与工艺流程和高度可重入等特征的可重入制造系统时, Petri网模型很难得出解析的控制与决策结果, 而排队网络则需要忽略所有无法用排队序列描述的系统动态. 此外, 这两种离散事件模型的解算复杂度会随着制造系统复杂度的提升指数增加, 这为智能制造的控制与决策带来了很大的困难.

双曲型偏微分方程 (partial differential equation, PDE)是近年提出的一种面向可重入制造系统的连续间逼近模型. 它从总体角度描述了制造系统产品密度动态变化特性. 相比上述离散事件模型, 双曲型PDE模型的解算复杂度与系统维度和参数个数无关, 且能非常好地体现制造系统的瞬态特性. 国内外学者针对制造系统的双曲型PDE模型, 已经提出大量数值与控制算法, 取得了一定的研究进展. 但是可重入制造系统是一个典型的多因素、多扰动的复杂系统, 其内外部环境存在各种不确定性, 例如: 每台设备有一定概率制造出不良产品、出现紧急订单的突发事件、发生故障等等. 此外, 可重入制造系统的鲁棒控制存在着一些挑战. 首先, 为了更好地调配资源,工业现场通常配备高带宽网络, 将人机物三者有机结合起来, 这也就是国家现在大力发展的工业互联网. 这种海量的连接使得各个生产场景不再孤立, 但是也会使整个制造工厂表现出多维非线性耦合的复杂动力学特性. 之前讨论的各种各样的不确定因素, 使得扰动在制造系统的建模问题中不可避免. 从系统工程的角度, 工业互联网也可以被视为典型的受扰动干扰和耦合非线性动力学的复杂网络, 复杂网络已经在近几十年来被广泛研究. 综合上述的因素, 据作者所知, 目前针对多生产线可重入制造系统, 如下图所示, 鲁棒控制问题还没有成熟的结果, 因此也就促使笔者开展这项研究.

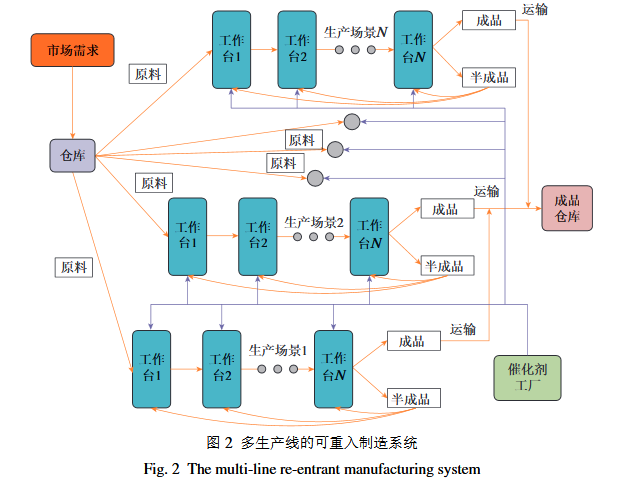
本文提出了一种智能鲁棒控制策略用以驱动上图所示的多生产线可重入制造系统平稳运行. 具体而言, 通过引入非线性的控制通道和考虑生产场景之间的耦合以及无处不在的扰动, 一种参数化和层次化的控制系统架构被提出以响应瞬间变化的市场需求. 对于反馈控制系统的设计, 考虑到模糊建模技术在处理系统非线性上的巨大成功, 本文建立了基于模糊模型的控制方程. 特别的, 本文提出了一种模糊鲁棒滑模并行控制器, 对系统中的不确定性和扰动表现出较强的鲁棒性. 理论分析也表明闭环制造系统能够在有限时间内就以指数速率收敛到预设的状态中. 该层次化控制方法有如下的特点:

1) 设计了一种层次化控制架构, 能够实时应对外界快速变化的市场需求和抑制系统中无处不在的扰动;

2) 控制器的设计被投影为凸优化问题, 从而在多项式时间内求解;

3) 针对连续时间PDE模型的滑模控制算法能够移除已有方法的限制, 应用于具有非线性控制通道和受扰动干扰的一般连续时间制造系统模型.

结论

本文为一类多生产线可重入制造系统设计了层次化架构和对应的鲁棒控制器. 基于以双曲型偏微分方程描述的连续模型, 本文在控制系统中引入了层次化的设计思想, 构造了一种模糊滑模控制器使得闭环制造系统能够有效抑制扰动并快速实现平稳运行. 针对控制器设计的无穷维特性, 本文提出了一种凸优化算法在多项式时间内近似求解控制器. 该层次化智能控制策略可以应用于具有海量工艺和复杂加工技术的场景, 如国家目前大力发展的半导体制造产业和复杂化工品生产领域.

作者简介

张春阳硕士研究生, 目前研究方向为智能控制理论与深度学习;高庆教授, 目前研究方向为智能系统、控制理论和工业互联网;吕金虎教授, 目前研究方向为工业互联网与复杂网络;陈巍教授, 目前研究方向为复杂系统;王健男讲师, 目前研究方向为复杂系统.

期刊介绍

《控制理论与应用》(Control Theory & Applications)是经国家科学技术部批准, 教育部主管, 由华南理工大学和中国科学院数学与系统科学研究院联合主办的全国性一级学术刊物, 1984年创刊, 月刊, 国内外公开发行. 《控制理论与应用》是中国科学引文数据库首批统计源期刊之一，中文核心期刊，入选中国精品科技期刊顶尖学术论文F5000项目，中国科协自动化学科领域高质量科技期刊目录以及中国科协百篇优秀科技论文遴选计划，2021年入选广东省高质量科技期刊建设项目，2022-2024年连续获得基金委资助（科技活动专项）.

期刊封面2.jpg 目录2.jpg