学习周报

姓名	郝丹萌	时间范围	2025.3.24-2025.3.30
周次	第十四周	研究方向	大模型高效参数微调

AWQ 量化详细

•  AWQ: 激活感知的权重量化

• 2.1 观点 1-权重并非同等重要，需要基于激活分布来挑选权重的显著通道

• 2.2 观点 2-对显著权重进行放大可以降低量化误差

• 2.3 算法-计算缩放因子 s

1. 摘要

本文提出了激活感知权重量化 (AWQ)，这是一种适合硬件的 LLM 低位权重（比如 w4）量化方法。AWQ 发现，并非所有 LLM 权重都同等重要，仅保护 1% 的显著权重便能大幅减少量化误差。而要识别显著权重通道，应参考的是激活分布而非权重分布。为了避免硬件效率低下的混合精度量化，我们通过数学推导得出，放大显著通道可以减少量化误差。AWQ 采用等效变换来放大显著权重通道，用于保留权重显著通道值，保留的比例通过离线收集激活统计数据确定。

AWQ 不依赖反向传播或重构，因此可以泛化到不同领域和模态而不会对校准集过拟合。AWQ 在各种语言建模和领域特定的基准测试（编码和数学）中优于现有方法。凭借更好的泛化性，它在指令微调语言模型以及多模态语言模型上首次实现了卓越的量化性能，多模态模型量化是前作 SmoothQuant 没有测试的领域。

2. AWQ: 激活感知的权重量化

量化技术通过将浮点数映射为低位整数，有效的减少 LLM 模型权重体积和推理成本。本节中，作者首先提出了一种仅针对权重的量化方法，通过保护更多“重要”权重，在无需额外训练（QAT）或回归的情况下提升模型精度。随后，作者引入了一种数据驱动的优化方法，来搜索减少量化误差的最佳缩放因子（见图 2）。

图 2b 展示了可以基于激活分布找到 LLM 中 1% 的关键权重，将这些关键权重保留为 FP16 可以显著提升量化后的性能（困惑度从 43.2（左图）降至 13.0（中图））。但这种混合精度格式在硬件上效率较低，基于激活感知原则，作者提出了 AWQ（右图）。AWQ 采用逐通道缩放方式，保护关键权重并减少量化误差。作者测试了 OPT-6.7B 模型上使用 INT3-g128 量化下的困惑度 PPL(越小越好)表现为 13.0，和前面的混合精度量化一样，说明 AWQ 量化算法有效。

2.1 观点 1-权重并非同等重要，需要基于激活分布来挑选权重的显著通道

作者观察到，LLM 中的权重并非同等重要：仅有 0.1%~1% 的小部分显著权重对模型输出精度影响较大。如果能保留这部分关键权重，其他权重使用低比特量化推理，那么就能在保持模型精度的前提下，大幅降低模型内存占用和提高推理速度。

这里有个问题是，哪部分权重通道更重要呢？通常评估权重重要性的方法是查看其大小或 L2-范数（所有权重平方和的平方根） (Han 等，2015；Frankle 和 Carbin，2018)，但在量化推理中也是这样吗？为此，作者做了三个对比实验来判断挑选显著权重方法的有效性，结果发现保留大范数的权重通道（即基于 W 的 FP16%）对量化性能的提升有限，跟随机选择通道带来的提升类似。详细对比结果见表 1 所示：

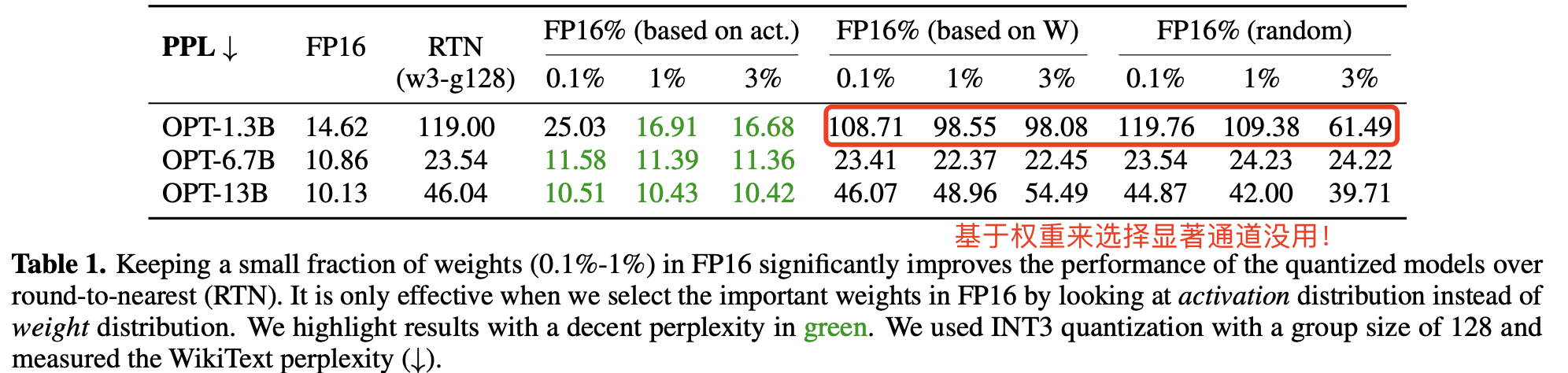
RTN 量化的核心思想是简单地将每个数值舍入到目标精度下的最接近值，量化缩放系数计算公式为 $\Delta =\frac{\text{max}-\text{min}}{2^n-1}$。

但有趣的是，作者发现基于激活值大小来选择权重可以显著提升性能！即使只保留 0.1%-1% 的通道为 FP16。推测是激活值较大的的输入特征通常更重要，而保留相应的权重为 FP16 可以更好地保护这些特征，从而提升模型性能。

具体实现上，作者是对激活值的每一列求绝对值的平均值，然后把平均值较大的一列对应的通道视作显著通道，保留 FP16 精度。

到这里可以总结出一个重要结论：LLM 权重并非同等重要，只有 0.1%~1% 的小部分显著权重对模型输出精度影响较大，又因为幅度较大的输入特征通常更重要，因此需要基于激活分布来挑选权重的显著通道。

局限性：尽管保留 0.1% 的权重为 FP16 可以提升量化性能，且不会显著增加模型的总位数，但混合精度的数据类型会推理系统实现复杂化。因此还需要找到一种方法，可以保护这些关键权重同时又不用实际保留它们为 FP16。

2.2 观点 2-对显著权重进行放大可以降低量化误差

论文描述是基于激活感知缩放保护关键权重 Protecting Salient Weights by Activation-aware Scaling，不是很清楚，这里我换了一种表达。

作者提出一种替代方案，通过逐通道缩放减少关键权重的量化误差，避免硬件效率问题。

量化误差分析

从权重量化带来的误差分析入手。假设一个权重组或块 $\mathbf{w}$，其线性操作可写为 $y=\mathbf{wx}$，而量化后的对应形式为 $y=Q(\mathbf{w})\mathbf{x}$，由此可定义量化函数为：

$$Q(\mathbf{w})=\Delta \cdot \text{Round}\left(\frac{\mathbf{w}}{\Delta }\right),\Delta =\frac{\max (|\mathbf{w}|)}{2^{N-1}}\text{\hspace{1em}(1)}$$

其中，$N$ 是量化位数，$\Delta$ 是由绝对值的最大值确定的量化缩放系数。

现在考虑对于一个权重元素 $w\in \mathbf{w}$，如果我们引入缩放因子 $s$，并在量化过程中将权重 $w$ 与 $s$ 相乘，同时将激活 $x$ 以同样的缩放因子 $s$ 逆向缩放！即 $Q(w\cdot s)(x/s)$，引入缩放因子之后的新线性操作函数形式变为：

$$Q(w\cdot s)\cdot \frac{x}{s}={\Delta }^{\prime }\cdot \text{Round}\left(\frac{ws}{{\Delta }^{\prime }}\right)\cdot x\cdot \frac{1}{s},\text{\hspace{1em}(2)}$$

虽然公式 1 和公式 2 在数学上是“等效”的，但是带来的精度损失是不一样的。

$\Delta ’$ 是在应用 $s$ 之后的新量化缩放系数。作者通过实验发现：

1. 来自 $\text{Round}(\cdot )$ 的期望误差（记为 $\text{RoundErr}(\cdot )$）不变：由于舍入函数将浮点数映射到整数，误差大致在 $[0,0.5]$ 范围内均匀分布，导致平均误差约为 0.25，即 $\text{RoundErr}(\cdot )\sim 0.25$。

2. 对单个元素 $w$ 进行缩放通常不会改变 $\mathbf{w}$ 组的最大值。因此可以得出 $\Delta ’\approx \Delta$ 的结论；

3. 由于 $\Delta$ 和 $x$ 以 FP16 表示，因此它们没有量化误差。

因此，方程 (1) 和 (2) 中的量化误差可以表示为公式（3）：

$$\text{Err}(Q(w)x)=\Delta \cdot \text{RoundErr}\left(\frac{w}{\Delta }\right)\cdot x$$$$\text{Err}\left(Q(w\cdot s)\left(\frac{x}{s}\right)\right)={\Delta }^{\prime }\cdot \text{RoundErr}\left(\frac{ws}{{\Delta }^{\prime }}\right)\cdot x\cdot \frac{1}{s}\text{\hspace{1em}(3)}$$

两个误差相除，可得新误差与原始误差的比率为 $\frac{\Delta \prime }{\Delta }\cdot \frac{1}{s}$。因为 $\Delta \prime \approx \Delta$ 且 $s>1$，则可推公式（2）的误差小于公式（1）。因此，量化时对显著权重进行放大即引入缩放因子 $s$，是可以降低量化误差的。

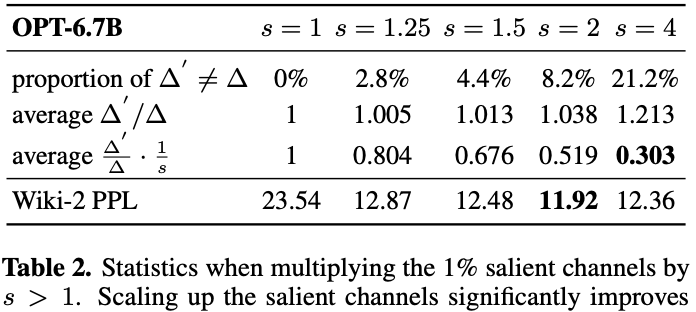
表 2 的实验结果直接证明了量化时对显著权重进行放大，是可以降低量化误差的，同时，在保护显著通道时，我们还需考虑非显著通道的误差。

转载本文请联系原作者获取授权，同时请注明本文来自郝丹萌科学网博客。

链接地址：https://wap.sciencenet.cn/blog-3622922-1479995.html?mobile=1

收藏

分享