 精选
精选
文章亮点介绍
1. 本文从底层原理角度讨论分析了线性及广义线性框架下,数据前期融合与后期融合的关系与差异,并给出了其等价性条件及证明。
2. 本文给出了一种数据驱动的融合模型效果评估方法,同时给出了优势算法反转临界样本量阈值点的估算方法,揭示了不同融合方法的样本量优势区间。
3. 本文提出了一种融合方法选择范式,缓解了重复实验带来的方法选择成本高的问题。
文章介绍
1. 研究背景及目的
数据采集技术的发展促进了用于表征复杂场景的多模态数据激增。为了追求分析的准确性,越来越多的研究者采用不同的数据融合方法增强模型的表征能力。目前主流数据融合方法分为前期融合、中期融合和后期融合。如何为特定任务选择合适的融合方法是一个重要问题,影响着模型的计算成本与性能。当前研究大多通过多次实验,对比不同融合方法的整体性能,进而选取合适的数据融合方法,但伴随而来的是高昂的计算成本。
图一展示了本文的整体研究框架。本文在广义线性的框架下,从融合机制、样本量及融合效果角度对比了前期融合、后期融合和渐进融合的异同。在此基础上提出了数据驱动的模型精度估算方程,分析不同融合模型精度发生逆转的临界样本量阈值,并给出了融合方法选择范式,可有效降低融合方法选择的计算成本。
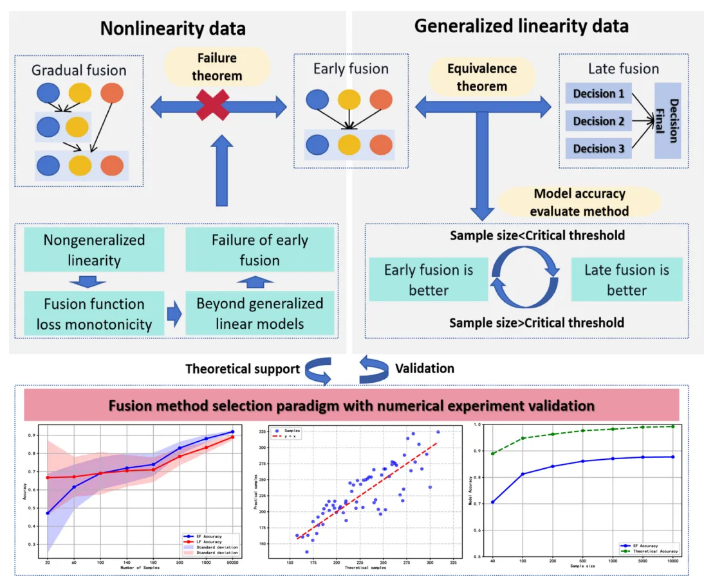
图1.本文研究框架。
2. 模型及结果分析
利用特征维度、样本量、模态数等数据属性构造融合模型精度评估方程:
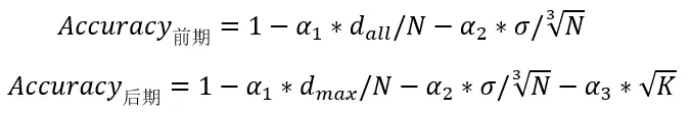
基于精度评估方程计算临界样本阈值:
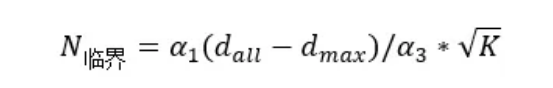
通过最小化理论和实际样本临界阈值误差的优化方法估计参数𝛼1和𝛼3,通过最小化理论和实际的前期融合模型精度误差的优化方法估计𝛼2。
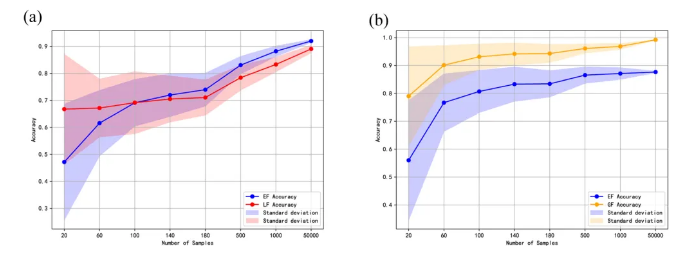
图2.100次仿真实验结果的对比:(a) 前期融合与后期融合模型精度仿真实验对比;(b) 前期融合与渐进融合模型精度仿真实验对比。
图2展示了100次仿真实验结果的对比,上述估算公式可有效表示模型准确率随训练样本数量的变化趋势。
融合方法选择范式:
从样本中进行随机抽样,并且每次抽样后计算数据信噪比;
利用广义线性模型构建前期融合与后期融合模型,并用抽样样本进行训练,记录模型精度,同时计算抽样样本下的模型理论精度;
将模型精度与理论精度进行比较,若模型精度与前期或者后期融合理论精度的最大误差不超过20%,则认为该任务可以用基于广义线性的前期或者后期融合方式进行,跳转到步骤d;否则跳转到步骤e。
计算优势算法反转临界阈值点,若训练样本量大于临界阈值点,则选择前期融合方法;否则,选择后期融合方法。
认为该任务中特征与标签间为非线性关系,并且以95%的置信度无法使用基于广义线性的前期或者后期融合进行,需要考虑融合非线性先验知识的渐进融合方法。
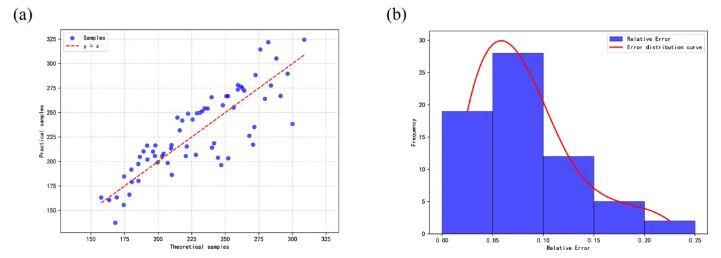
图3.(a) 临界阈值点在100次仿真实验中估算值与真实值;(b) 临界阈值点估算值与真实值的相对误差分析。
图3展示了样本临界阈值点的估算值和真实值。结果表明我们所提的方法选择范式可以有效估算算法性能发生翻转的临界阈值点,并判别特定场景下的融合方法适用性。
3.讨论与总结
本文中,我们提出了一个融合方法选择范式,为执行特定任务之前的模型选择提供了理论依据。在广义线性框架下对比了不同融合方法,揭示了在样本量充分大时,前期融合具有最优融合效果;而在特征维度高、样本量稀少时,后期融合往往具有更优融合效果,增强了对不同融合方法机理层面的理解。在理论的指导下构建了包含样本量、特征量和模态数的模型精度评估方程,并分析了模型的性能优势逆转的样本临界阈值,揭示了不同模型的适用样本量条件。最后,基于精度评估方程提出了融合方法选择范式。数值实验结果表明,该方法能够可靠地判别不同融合方法在特定问题下的适用性,有效缓解了重复实验带来的方法选择成本高的问题。
作者介绍
第一作者:刘子琦
北京航空航天大学数学科学学院,博士研究生,主要研究方向为复杂网络理论和多模态数据融合方法及其在疾病精准诊疗中的应用。
通讯作者:殷子樵
北京航空航天大学人工智能学院助理教授,研究生导师,长期从事数学、医学与人工智能的交叉领域研究,研究集中于人工智能算法的数理基础、面向医学场景的精准智能算法及仿生智能算法设计等前沿研究方向。
作者:米志龙
北京航空航天大学。
通讯作者:郭炳晖
北京航空航天大学人工智能学院副教授,博士生导师,数学信息与行为教育部重点实验室副主任,长期从事数学与信息交叉科学中人工智能基础问题、群体智能及进化智能理论与技术、人工智能在生命科学及金融学中的应用等前沿问题研究。
作者:郑志明
中国科学院。
原文出自 Mathematics 期刊:https://www.mdpi.com/2227-7390/13/8/1218
期刊主页:https://www.mdpi.com/journal/mathematics
Mathematics 期刊介绍
主编:Francisco Chiclana, School of Computer Science and Informatics, De Montfort University, UK
期刊主题涵盖纯数学和应用数学所有领域,重点发表代数与逻辑、几何与拓扑、数学分析、统计与运筹学、应用数学,包括数学与计算机科学、控制理论与力学、数学生物学、数学物理、金融数学等数学在其他各学科应用的文章。现已被 SCIE (Web of Science)、Scopus 等重要数据库收录,JCR category rank: 21/490 (Q1)。
2023 Impact Factor:2.3
2024 CiteScore:4.6
Time to First Decision:18.3 Days
Acceptance to Publication:1.9 Days


转载本文请联系原作者获取授权,同时请注明本文来自MDPI开放科学科学网博客。
链接地址:https://wap.sciencenet.cn/blog-3516770-1489601.html?mobile=1
收藏

