文章导读
卡尔曼滤波器由美国数学家鲁道夫•卡尔曼于1960年提出,利用系统状态的先验估计与实时测量值之间的加权平均来进行状态更新,成为解决线性高斯系统状态估计问题的经典方法,尤其是在导航和控制领域中获得了广泛应用。然而,随着工业设备的不断升级,许多系统的动态关系呈现非线性,并且噪声往往不是高斯分布的,这种非对称的噪声分布特性与传统方法假设的对称高斯模型形成显著冲突,这使得传统卡尔曼滤波器在这些复杂环境下无法保持其最优性,性能显著下降。
为了解决上述问题,研究人员发展出了多种改进算法,如扩展卡尔曼滤波、无迹卡尔曼滤波等,但它们在处理高非线性和非高斯噪声时仍然面临挑战——特别是在系统动力学方程和观测模型存在非对称结构时,传统线性化方法会破坏模型内在的对称性特征,导致估计偏差加剧。鉴于此,来自西南大学电子信息工程学院的王世元老师团队在 Symmetry 期刊发表了文章,提出了一种新型非线性滤波器——基于广义损失的广义转换滤波器 (Generalized Loss-based Generalized Conversion Filter, GLGCF)。该滤波器基于广义损失 (Generalized Loss, GL) 函数,对传统广义转换滤波 (Generalized Conversion Filter, GCF) 模型进行了重构,在重尾噪声和混合噪声环境下均呈现出良好的鲁棒性。
研究过程与结果
本文首先回顾了非线性卡尔曼滤波器在各领域的研究进展,分析了实际工程应用中非高斯噪声的普遍性及其影响。在梳理现有非高斯噪声处理方法的基础上,探讨了GL函数在非高斯噪声处理中的独特优势,特别是其灵活性和适应性特征。基于GCF的滤波框架,本文通过引入非线性回归模型将GL函数融入到GCF的滤波更新过程中,建立GL函数与状态量估计之间的非线性映射关系,最终获得了基于GL函数的最优状态量估计结果。
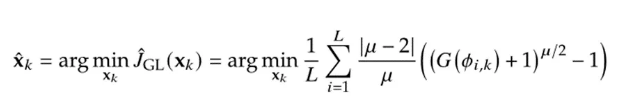
在基于GCF的滤波框架的基础上,引入负对数似然函数的参数优化机制,实现了GLGCF算法中GL函数形状参数的自动寻优,避免了更新过程中手动调参的繁琐过程,提升了算法的自适应能力。
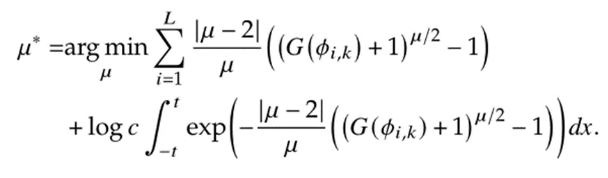
在本文的实验仿真部分,采用了协同转向目标跟踪模型,对所提出的GLGCF算法在重尾噪声和混合噪声环境下的滤波性能进行了系统性评估,与多种经典滤波算法进行了对比分析,包括粒子滤波器 (Particle Filter, PF)、无迹卡尔曼滤波器 (Unscented Kalman Filter, UKF)、容积卡尔曼滤波器 (Cubature Kalman Filter, CKF)、GCF以及最大相关熵广义转换滤波器 (Maximum Correntropy GCF, MCGCF)。结果显示,在重尾噪声 (见图1) 和混合噪声 (见图2) 环境下,GLGCF算法在目标位置估计精度和目标速度估计精度均优于上述对比算法,能够更准确地捕捉目标的动态变化,展现出更强的适应性和稳定性。
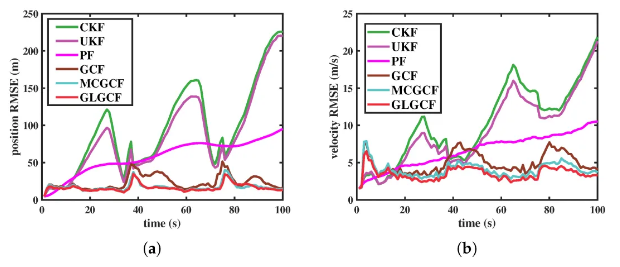
图1. 重尾噪声下不同滤波器在协同转向目标跟踪模型估计中的均方根误差。

图2. 混合噪声下不同滤波器在协同转向目标跟踪模型估计中的均方根误差。
研究总结
本文提出了一种广义转换滤波器的扩展版本——基于广义损失函数的广义转换滤波器。针对传统广义转换滤波器在高斯噪声环境下表现良好但在非高斯噪声中性能显著下降的问题,本研究通过非线性回归模型重构了广义转换滤波器的算法框架,采用广义损失函数替代传统的最小均方误差准则进行系统状态估计。最后,通过目标跟踪模型的仿真例子验证了所提算法的有效性和鲁棒性。本文的研究内容为拓展非线性卡尔曼滤波器的理论及其在非高斯噪声环境下的应用提供了参考。
原文出自 Symmetry 期刊:https://www.mdpi.com/2073-8994/17/3/334
期刊主页:https://www.mdpi.com/journal/symmetry
Symmetry 期刊介绍
主编:Sergei Odintsov, Institute of Space Sciences (ICE-CSIC), Spain
期刊主题涵盖了所有科学研究中有关对称/非对称现象的理论和应用研究,主要包括数学、计算机、工程与材料、物理学、生命科学、化学等领域的最新进展。期刊已被Scopus、SCIE (Web of Science)、CAPlus/SciFinder等多家知名数据库收录。
2023 Impact Factor:2.2
2023 CiteScore:5.4
Time to First Decision:17.3 Days
Acceptance to Publication:3.7 Days


转载本文请联系原作者获取授权,同时请注明本文来自MDPI开放科学科学网博客。
链接地址:https://wap.sciencenet.cn/blog-3516770-1480123.html?mobile=1
收藏

