 精选
精选
文章亮点介绍
在强化学习算法中,离策略学习是一种关键设置。近年来,即便在结合线性函数近似和引导式 (bootstrapping) 的情况下,基于值的强化学习中的离策略学习的稳定性也得到了保证。收敛速度分析目前是一个热点话题。然而,各种学习算法的收敛速度差异显著,分析其原因仍然是一个未解决的问题。在本文中,作者提出了一种简化版的收敛速度,用于生成通用的离策略时序差分学习 (off-policy temporal difference learning, off-policy TD) 算法。作者强调,影响收敛速度的主要因素是关键矩阵的最小特征值。此外,作者对各种离策略学习算法在不同数值场景中的影响因素进行了对比分析。实验结果验证了所提出的因素,该因素可作为设计更高效学习算法的基准。
文章介绍
研究背景及目的
离策略学习通过行为策略生成经验数据,并学习不同的目标策略。使用线性函数近似的off-policy TD学习在一些被称为“致命三角”的反例中可能会发散[1]。其根本原因在于off-policy TD的关键矩阵不一定是正定的[2]。在过去30年中,主要的研究集中在通过构建正定矩阵来确保离策略算法的收敛性,例如bellman residual (BR) [3]、gradient TD (GTD) [4]、fast gradient TD (GTD2)、TD with gradient correction (TDC) [5]、emphatic TD (ETD) [2]和modified Retrace (MRetrace) [6]。
近期,由于收敛性的保证,越来越多的研究开始关注强化学习算法的收敛速度分析。Dalal等[7]提出了一次时间尺度时序差分学习算法的期望收敛速度和高概率收敛速度。Dalal等[8]、Gupta等[9]、Xu等[10]以及Dalal等[11]获得了两次时间尺度时序差分学习算法的高概率收敛速度。Durmus等[12]提出了线性随机近似法在固定步长下的紧高概率界。对于控制设置,Xu和Liang[13]提出了Greedy-GQ的收敛速度,Zhang等[14]提出了投影SARSA的收敛速度,Wang等[15]提出了分布鲁棒Q学习的高概率收敛速度。
然而,上述分析并没有回答以下问题:这些算法中哪一个收敛更快?我们应该选择哪一个?本文的目的是直观的比较收敛速度。
假设与重要推论
Assumption 1:通用TD算法的关键矩阵𝐀是正定的。
Assumption 2:序列{𝑟𝑡, 𝜙𝑡, 𝜙′𝑡}具有一致有界的二阶矩。令ℱ𝑡 = 𝜎(𝜃1,𝑀1,…,𝜃𝑡−1,𝑀𝑡),则存在一个常数𝐶𝑠>0,使得以下条件成立:

Assumption 3:步长序列𝛼𝑡满足𝛼𝑡∈(0,1),式1和式2。
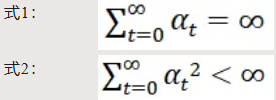
Assumption 4:特征矩阵Φ列满秩。
Assumption 5:假设每个算法共享相同的特征矩阵、相同的行为策略、相同的目标策略、相同的初始参数𝜃0、相同的常数𝐶𝑠和相同的学习率序列𝛼𝑡。
Corollary 1 (影响收敛速率的主要因素):假设满足Assumption1—5。从期望收敛速率的角度来看,影响收敛速率的主要因素是关键矩阵𝐀的最小特征值½𝜆min(𝑨+𝑨⊤)。此外,关键矩阵的最小特征值越大,算法的收敛速率就越快。
讨论与总结
基于所提出的收敛速度来构建通用的离策略时序差分学习算法,本文证明了影响收敛速度的主要决定因素是关键矩阵的最小特征值。聚焦于该因素将有助于开发收敛速度更快的离策略学习算法。
本文的局限性包括以下几个方面:(1) 本文假设所有算法的学习率相同,然而在实际中,不同算法的适用学习率范围不同。(2) 本文未考虑固定学习率的情景。(3) 本文重点研究了学习预测,未涉及学习控制。
未来的工作需要解决上述限制,并探索如何基于本文的结论设计更快速的算法。
作者介绍
陈兴国
南京邮电大学江苏省大数据安全与智能处理重点实验室。研究方向:强化学习。
秦旺荣
南京邮电大学江苏省大数据安全与智能处理重点实验室。研究方向:强化学习。
巩宇
南京邮电大学江苏省大数据安全与智能处理重点实验室。研究方向:强化学习。
杨尚东
南京邮电大学江苏省大数据安全与智能处理重点实验室。研究方向:强化学习、多智能体系统。
王文浩
国防科技大学电子工程学院。研究方向:强化学习、网络安全。
阅读英文原文:https://www.mdpi.com/2227-7390/12/18/2930
期刊主页:https://www.mdpi.com/journal/mathematics
Mathematics 期刊介绍
主编:Francisco Chiclana, School of Computer Science and Informatics, De Montfort University, UK
期刊主题涵盖纯数学和应用数学所有领域,重点发表代数、几何和拓扑、函数插值、差分和微分方程、计算和应用数学、概率与统计、数学物理、动力系统、工程数学、数学和计算机科学、数学生物学、网络科学、金融数学、以及模糊集、系统和决策等相关领域的文章。现已被SCIE (Web of Science)、Scopus等重要数据库收录,JCR Category Rank: 21/489 (Q1)。
2023 Impact Factor:2.3
2023 CiteScore:4.0
Time to First Decision:18.3 Days
Acceptance to Publication:1.9 Days


转载本文请联系原作者获取授权,同时请注明本文来自MDPI开放科学科学网博客。
链接地址:https://wap.sciencenet.cn/blog-3516770-1468101.html?mobile=1
收藏

