时称的浮力可以以压强、压力概念为基础推导出来

--暨浮力不应再称定律或原理

李务伦

现行教材浮力的成因是“压力差”，其大小是排开流体所受到重力的负值。这种詮释在《浮力的“压力差”成因解释是否不妥，https://blog.sciencenet.cn/blog-3433895-1478450.html》等已经谈过其不妥，并叙述其原因，这里不再重复。谈这不妥源于之前已利用万有引力定律导出来了浮力的存在，下面再用常用的知识讨论浮力的形成，以建立科学的浮力形成观念。如有不当敬请批评指正！

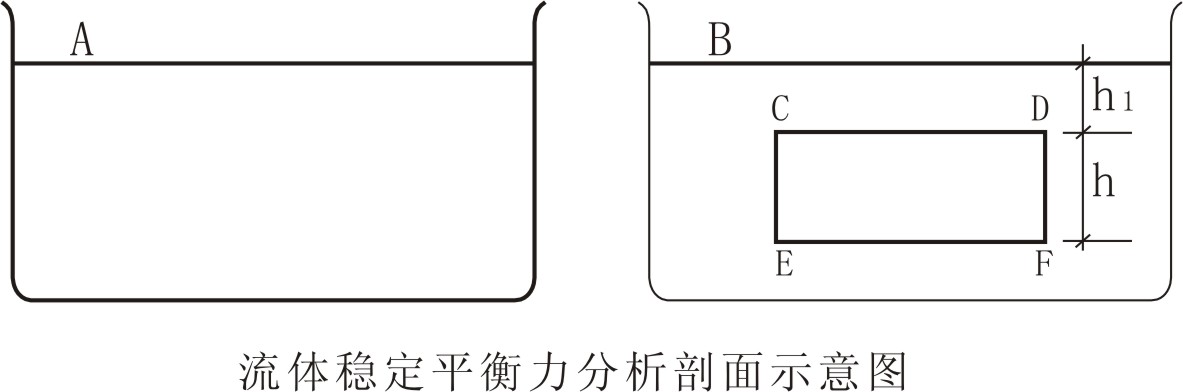
图1

图1 A中的容器盛有密度为ρ，处于静止状态的流体，所以任意一质点都处于稳定平衡状态。同一深度上压强相等，压力相等（球巨大球内性质的极限表达）。虽然流体中某一深度点的压强各向相等，但对等的是各向对该点的压强也是相等的。如果确定某一方向对该点的压强为正，对等的与这一方向相对的压强即为负。而各向相等的压强是由上部液体的重力对其下部的作用形成的，因此下部的液体必提供同等的压强以达到液体内部的稳定与平衡。因此沿任意一垂直流体表面方向，在其任意一点上来自上部物质产生的压强设为负，那么来自其底部的压强即为正，且同值，这一同值符合作用力与反作用力原理。后面提到压强方向就依这一约定。

在A中任意划定一如图1 B中所示的长方体区域。对于划分的长方体区域也存在上表面CD和下表面EF，上、下表面面积都为S，在其深度上的压强值分别为：ρgh₁和ρg(h₁+h)。上表面CD和下表面EF又可分为朝向流体表面的面和朝向壁底的面，朝向流体表面的以上两面称为上表面CD上和下表面EF上，朝向壁底的平面两面称为上表面CD下和下表面EF下。根据上面压强的约定，作用于上表面CD上和下表面EF上的压强分别为：-ρgh₁和-ρg(h₁+h)；作用于上表面CD下和下表面EF下液体的压强分别为：ρgh₁和ρg(h₁+h)。因此上表面CD上和下表面EF上来自上部液体的压力分别为-ρgh₁S和-ρg(h₁+h)S；上表面CD下和下表面EF下，来自下部液体反向压力分别为ρgh₁S和ρg(h₁+h)S。-ρgh₁S和ρgh₁S，-ρg(h₁+h)S和ρg(h₁+h)S是两对作用力与反作用力。

这样以来划定区域对下表面EF下部流体的作用压力差为：

F_差下=-ρg(h₁+h)S-(-ρgh₁S)=-ρghS…（1）

下部流体对下表面EF上部划定区域反作用力的压力差为：

F_差上=ρg(h₁+h)S-ρgh₁S=ρghS…（2）

两式中hS为划定区域长方体的体积V，ρhS划定区域的质量为m，于是上述两式又可分别表述为：

F_差下=-ρgV=-mg…（3）

F_差上=ρgV=mg…（4）

上面两式中mg是质量为m的划定区域在地球引力场中受到的重力值，前面一式（3）表示了划定区域液体对下表面EF下部液体的作用力，后一式（4）表示了划定区域受到的下表面EF下部液体对其反作用力，二者等值而反向。这一对等值而反向的作用力和反作用力维护着流体内部的平衡稳定。这二力在《浮力的“压力差”成因解释是否不妥》等以往博客中前者称稳定平衡力，后者称稳定平衡支撑力。

前述划定区域置换成异于流体密度ρ_i的物质时，也用同样的分析方法进行分析。划定区域物质置换后，图示的垂直长方体上、下表面的区域压强和压力，会因长方体密度的改变而发生改变，而其外部区域则与前面一样保持不变。在垂直长方体上下表面的区域内，上表面CD以上液体对上表面CD压强仍为ρgh₁，过上表面CD，因密度的改变至下表面EF压强为ρgh₁+ρ_igh。因此上表面CD上来自上部液体的压强为-ρgh₁，其上压力为-ρgh₁S；下表面EF上来自上部液体和密度为ρ_i长方体物质的压强为-ρgh₁-ρ_igh，其上压力为-ρgh₁S-ρ_ighS。而上表面CD上的压强-ρgh₁直接作用于密度为ρ_i长方体的上表面，密度为ρ_i长方体上表面必有与之相对的方向相反的压强ρgh₁，密度为ρ_i长方体上表面对上表面CD下的作用力为ρgh₁S。下表面EF下，由于与外部连通，外部与下表面EF下同一平面内压强为ρgh₁+ρgh并没有改变，所以密度为ρ_i长方体下表面下表面EF下压强也为ρgh₁+ρgh，下表面EF下压力仍为ρgh₁ρS+ρghS。

由上的分析知，上表面CD下和下表面EF下两者上的压力的压力差没有改变，仍为式（2），因此密度为ρ_i长方体下的液体，对密度为ρ_i长方体底面作用力仍为（4）。对于划定区域置换成异于流体密度ρ_i的物质后，也由上的分析知，原划定区域压力对对下表面EF下部流体的压力差或作用力变为：

F_差下i=-(ρgh₁+ρ_igh)S-(-ρgh₁S)=-ρ_ighS=-ρ_igV=-m_ig  i=1或2…（5）

式（5）中ρ₁＜ρ＜ρ₂。在进行下面的讨论前，先讨论式（5）中ρ_i与流体密度相等时，和式（1）相同。所以即便换了其它物质，根据上面的讨论上述各种力不变，所有质点仍处于稳定平衡状态。

当流体密度ρ大于置换划定区域的长方体ρ₁时，式（5）力的绝对值小于式（3）力的绝对值，也小于式（4）的力，密度为ρ₁时的长方体显然不再稳定。式（4）力克服密度为ρ₁时的长方体式（5）的力，具有向流体表面运动的合力-m₁g+mg，如果该合力再次克服长方体与流体间的粘滞力后，将上升，否则不动。

当流体密度ρ小于置换划定区域的长方体ρ₂时，式（5）力绝对值大于式（3）力的绝对值，也大于式（4）力，密度为ρ₂时长方体显然也不稳定。式（4）所表达力不敌长方体式（5）力，具有向壁底运动的合力-m₂g+mg，如果该合力再次克服长方体与流体间的粘滞力后，将下降，否则不动。

通过以上的分析，异密度物体取代相应位置流体后，破坏了原有位置处的力的平衡，而对取代位置的反作用力并没有因此而改变。这一反作用力对小密度物而言，克服小密度物的重力而上升；对大密度物而言，大密度物重力克服反作用力而下降，并使其所居位置再次恢复平衡，所以这一反作用力式（4）才是浮力的成因和本质。因此浮力的定义笔者认为应是：物体浸入取代另一密度某一位置物质后，原有的力的平衡被破坏，但承载原处物质平衡的反作用力并不因此而改变，这一不变的反作用力即为浮力，其值等于原处物质所受重力的负值。而此处给出浮力这样一个定义时，之所以没有特指流体，根据前面的讨论，可知这浮力是不依赖物质的相态而存在。这也与之前博客推出的浮力定理相一致，同时有益于中学生在没有引力场概念时的浮力概念建立，为后面再认识浮力源于万有引力打下基础。

时下流行的对浮力有以下两种表达：1、“浮力的大小等于物体排开的液体所受的重力，方向竖直向上”；2、“浮力指物体在流体（包括液体和气体）中，各表面受流体（液体和气体）压力的差（合力）”。这两条时称为阿基米德定律和形成原因。根据前面的分析二者都有一定道理，但又都存在不足。

通过以上分析，发现可以通过数理知识，可以推导出浮力的形成的数理根据。所以笔者认为可以补足浮力没有数理根据的局面，因此浮力再称原理或定律应不再恰当，而称浮力定理应是不错的选择！

2025年4月21日于哈尔滨香坊

转载本文请联系原作者获取授权，同时请注明本文来自李务伦科学网博客。

链接地址：https://wap.sciencenet.cn/blog-3433895-1482785.html?mobile=1

收藏

分享