浮力的“压力差”成因解释是否不妥
李务伦
浮力的成因的解释以往共识是：“液体对浸入其中的物体上下表面的压力差”。这种解释是否妥当呢？笔者根据万有引力定律对浮力形成的探讨过程，这种解释应该是不全面、不妥当，甚至是错误的。下面就这问题做陈述，并请老师们给予指导，对此首先表示感谢！
远离地球引力场或远离一切星球引力场的相当量的可塑物质，所有质点在万有引力的作用下将同其它星球一样成为球体，也同其它星球一样并有独立的引力场。单密度可塑物质形成均匀球体；多密度物质形成具有同心球层，且由内而外密度是逐渐减小的球体；在这些球体内，同半径的球面为等引力强度值球面，且任意点的引力强度方向指向球心；同半径球面为等压力面；同半径球面为等引力位面；球内所有质点均处于稳定平衡状态。这些在过往的博文中称之为球内性质。这是一切星体为球态的稳定、平衡的最基本性质和最基本动力，没有这一最基本动力谈其它问题应缺乏应有的基础。
1、从力的平衡谈浮力“压力差”的成因不妥切
图1
图1为多密度可塑物质形成的球体，在图示的球层中圈定了球形和旋转球台区域。所圈定区域范围密度与所在球层相同，内球层密度为ρA，外球层密度为ρB。圈定区域相当于浸入同等体积，同等形态，同样密度的物体。显然圈定区域，根据《谈一谈地球球内压力的计算https://blog.sciencenet.cn/blog-3433895-1441051.html》已给出计算公式，可以用这些公式计算圈定区域各自存在的压力差具体表达式，然具体计算公式与要解决的问题意义不大，故不给出具体表达式。尽管存在“压力差”，根据球内性质，图1中圈定区域处于稳定平衡状态，可见“压力差”解释浮力的形成并不妥切。为后面叙述方便，将此时的压力差称为稳定平衡压力差。同时也应看到小球的底球面或旋转球台底面任意点处的压力与该点向邻点压力相等，保持稳定平衡关系。
对图1各圈定范围，根据《浮力形成的万有引力定律又再计算再解释https://blog.sciencenet.cn/blog-3433895-1467553.html》一文的陈述，存在稳定平衡力和稳定平衡支撑力；稳定平衡支撑力等于稳定平衡力的负值。图1中小球的稳定平衡力分别为：
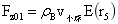……（1）
……（2）
旋转球台的稳定平衡力，由于以往没有给出具体结果。下面对图1外球层内的旋转球台，假设大球的球内物质密度相同的情况下，给出经积分计算后的结果：
……（3）
（3）式中前部中括号为旋转球台的体积，后一中括号后面分式为旋转球台的质心距球心的距离即后半部分的r7。对于含球层的情况也为旋转球台的质量乘以旋转球台质心的引力强度（已推算），即为圈定旋转球台的受力。内球层旋转球台的受力为：
……（4）
而以上公式相应的稳定平衡支撑力为：
，
，
，
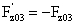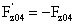。这些等式又可称为作用力和反作用力平衡方程。而当图1圈定范围的密度改变为ρxi，且大于或小于所在球层的密度。根据《浮力形成的万有引力定律又再计算再解释》，圈定范围的非稳定力分别为：
，
，
，
。
这些非稳定力较之稳定平衡力发生改变，密度大于所在球层密度，非稳定力绝对值大于稳定平衡力绝对值，否者相反。这样以来非稳定力绝对值大于稳定平衡支撑力时，图1中所示的小球和旋转球台，在球层黏度许可的情况下，将向球心运移，否者相反。由此而知稳定平衡支撑力才是浮力。以上从力的角度分析了浮力产生的成因，下面再从压力差上分析浮力的成因。
图1圈定区域密度的改变，不论是小球还是旋转球台，压力差也会改变。当圈定区域密度大于所在球层的密度，圈定范围内相同点上的压力，密度改变后的压力大于未改变前的压力，沿某一方向至小球底球面或旋转球台底面，较密度未改变前存在一个压力正增量。这种压力正增量一方面形成新的且大于稳定平衡压力差的新压力差，另一方面打破原有的压力平衡，促使小球或旋转球台向球心运动。当圈定区域密度小于所在球层的密度，则与上面的情况相反，不再赘述。为今后叙述方便，这种因密度改变形成的新压力差称为非稳定压力差。如果非稳定压力差减去稳定平衡压力差称为压力差增量，于是可有如下的陈述：压力差增量大于零，浸入物体在外围物质黏度形成的阻力许可的前提下向球心的方向运动；压力差增量小于零，在外围物质黏度形成的阻力许可的前提下向远离球心的方向运动。通过上面的讨论用压力差增量说是浮力的成因，也较勉强，因为压力差增量的产生，是密度的改变，因此笔者到是认为浮力的产生是密度差造成的，比压力差增量更为妥贴。同时即便不是流体，为固体只要存在密度差，浮力亦然存在，例如地质上的盐丘的存在就是全固体情况下所产生，所以时下流行的浮力定义或定律内涵存在严重的错误。而密度差的存在改变了图1球内引力场，下面再从引力场角度说明浮力产生的成因。
2、浮力引力场产生的引力场成因
图1中红色的线是含球层下的引力场中的引力线，这些引力线的方向均指向球心。对于单密度形成的引力场，也有同样的引力场线。但在均匀球内或含球层球内假如存在异密度ρxi的小球或旋转球台，它将改变球内引力场，这在以往的博文通过大球引力强度和小球增量描述了球内引力场的改变，见图2。在图2中，大球密度为ρ，它大于或小于小球的ρxi，大球半径为R，小球半径为r0。
图2
在假设小的密度和大球相同的前提下，以大球球心为坐标原点，大球球内大球引力场强度为：
……（5）
图2中的红色方向线为大球引力强度引力线。在式（5）小球质量没有完全计入或多计计，小球任意点多计入或少计的质量Δm=-ΔV(ρ-ρxi)，Δm多计质量（ρ＞ρx1）和少计的质量（ρ＜ρx2）引起的小球引力强度，分别命名为小球正增量和小球负增量，在图2中以小球心为坐标原点的极坐标系中，得小球增量如下两表达式。
…（6）
…（7）
以小球正增量为例，小球正增量在图2任意红色引力线上任意点有两个分量：平行红色引力线--小球平行正增量，垂直红色引力线--小球垂直正增量。小球平行正增量将大球内部分为两个区域：一个区域是半径为l的蓝球区域，小球平行正增量与大球引力强度同向，一个区域是半径为l的蓝球外部区域，小球平行正增量与大球引力强度反向，见图2中小箭头所示。小球垂直正增量上半球以OA为对称，在OA上为零，沿图示的圆背向的不断改变方向，到图示的水平红色引力线小球垂直正增量与AB平行；过此，以OB为对称，变为沿图示的圆相向的不断改变方向，到OB为零，图2中空心箭头表示了以上变化。
由此，小球平行正增量在蓝色球内小球增量使得该区域的任意点上的大球引力强度增加，蓝色球外部区域任意点上的大球引力强度减少，而以小球周边最大。这样以来，蓝色球内任意质点因引力强度增大，导致任意质点的压力增大，蓝色球外部任意质点的压力减小；球内任意质点引力位亦同。蓝色球球内压力较没有小球正增量时压力增大，蓝色球球外部分压力较没有小球正增量时压力减小。这样以来小球底部蓝色球为小球提供了上升的力，蓝色球外部减小了对小球上升的阻力。小球垂直正增量，上半球中心对称横向背向出现的引力强度，引起横向压力以松弛对称轴方向的压力，以小球周边最大；下半球中心对称横向相向出现的引力强度，引起横向压力以增加对称轴方向的压力。上半球松弛的压力为小球的上升提供进一步的可能，下半球增加的压力通过大球球心方向提供给蓝色球，进一步推动小球上升。
通过以上的分析，从引力场的角度分析出了导致低密度小球上浮的成因。以同样的方法，也可以分析出大密度小球下沉的成因。对于其它形态的物体，如图2中的虚线标注的旋转球台，不论旋转球台密度是大是小，与上的情况相同，蓝色的球不再是正球体如图虚线所示的椭球，其它不变。
3、结语
通过上面的讨论，结合以往浮力计算，搞清了浮力的成因与定量表达式数理根据。笔者之所以对浮力问题孜孜以求，是因为这一问题与目前裹足不前的地球动力学有着莫大关系。这是因为异密度的小球于大球中存在，可导致以下以不同参数的动力学：质心动力学、压力或压力梯度动力学、引力或引力梯度动力学、位能或位能梯度动力学、如果结合物质黏度还可以有应力积累动力学等。另一点就是将浮力由一个定律问题，转成为引力力学体系下的定理问题，为星球动力学扫清了一个障碍。
转载本文请联系原作者获取授权，同时请注明本文来自李务伦科学网博客。
链接地址：https://wap.sciencenet.cn/blog-3433895-1478450.html?mobile=1
收藏
