人们通过对惯性陀螺和股票市场大量的观察实验和实证研究,发现惯性陀螺随机游走与股票价格波动是具有相同性质及规律的布朗运动现象,均为“瞬时速度为白噪声”和“功率谱密度与频率的平方成反比”的布朗噪声(Brown Noise)或红噪声(Red Noise)。
但是,《随机信号分析》和《数理金融学》却采用了不同的研究方法,因而建立的数学模型相互矛盾,实际应用效果更是大相径庭,一个获得了成功应用,一个却获得了失败应用。
一、《随机信号分析》的“时间函数”研究方法及应用效果
图1为惯性陀螺中的随机游走(布朗噪声)和瞬时速度(白噪声)。
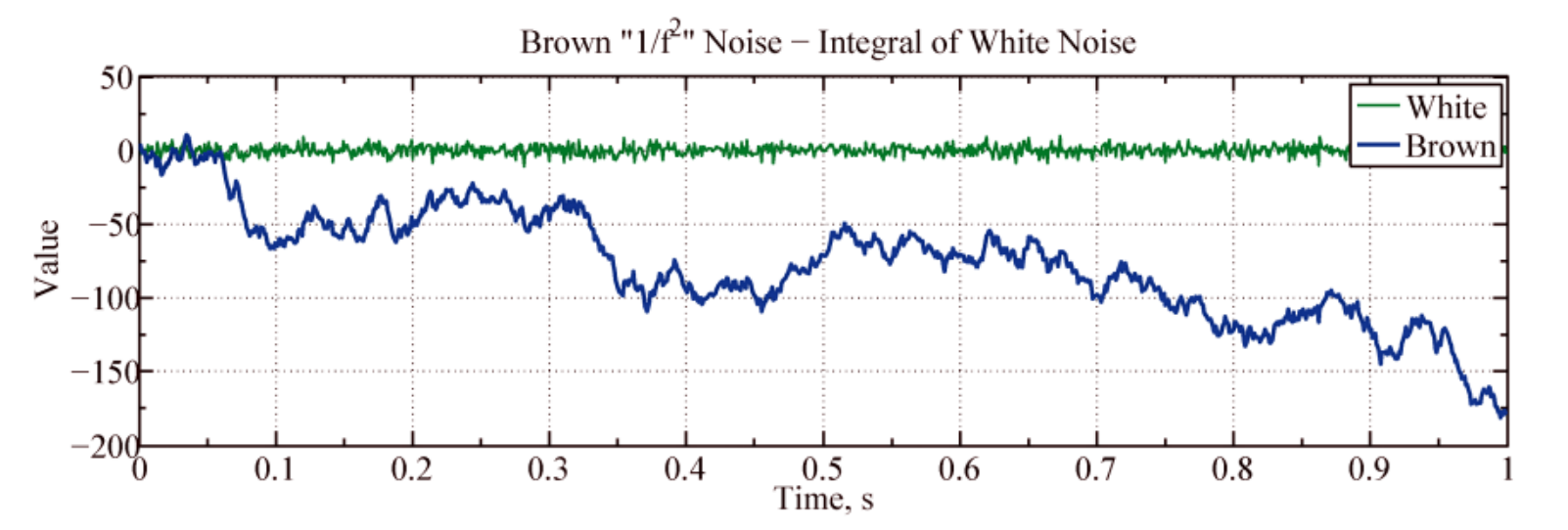
图1 惯性陀螺中的随机游走与瞬时速度
布朗噪声是通过对瞬时速度白噪声的积分获得的,显然,布朗噪声B(t)和白噪声n(t)均为时间t的函数。
假设n(t)为平均功率为σ2的白噪声,则随机游走(布朗噪声)B(t)可表示为:
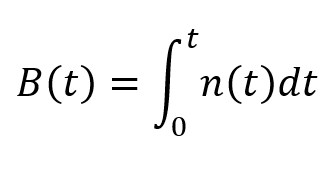
《随机信号分析》教科书、中华人民共和国国家军用标准《光纤陀螺仪测试方法(GJB2426A-2004)》和IEEE国际标准《IEEE Standard Specification Format Guide and Test Procedure for Single-Axis Laser Gyros(IEEE 647-2006)》就是将上式作为布朗噪声定义或惯性陀螺随机游走定义。
《随机信号分析》中的布朗噪声模型可正确描述、预测并补偿惯性陀螺仪中的随机游走误差,成功地解决了飞机、舰船、火箭、卫星、宇宙飞船和导弹的精确导航和精确制导问题,在航空、航天、航海和军事等领域获得了极为成功和广泛的应用。
二、《数理金融学》的“随机变量”研究方法及应用效果
图2为《量化交易:算法、分析、数据、模型和优化》书中给出的股票价格Pt和股票价格变化Dt =Pt+∆t - Pt 随时间t的变化曲线。
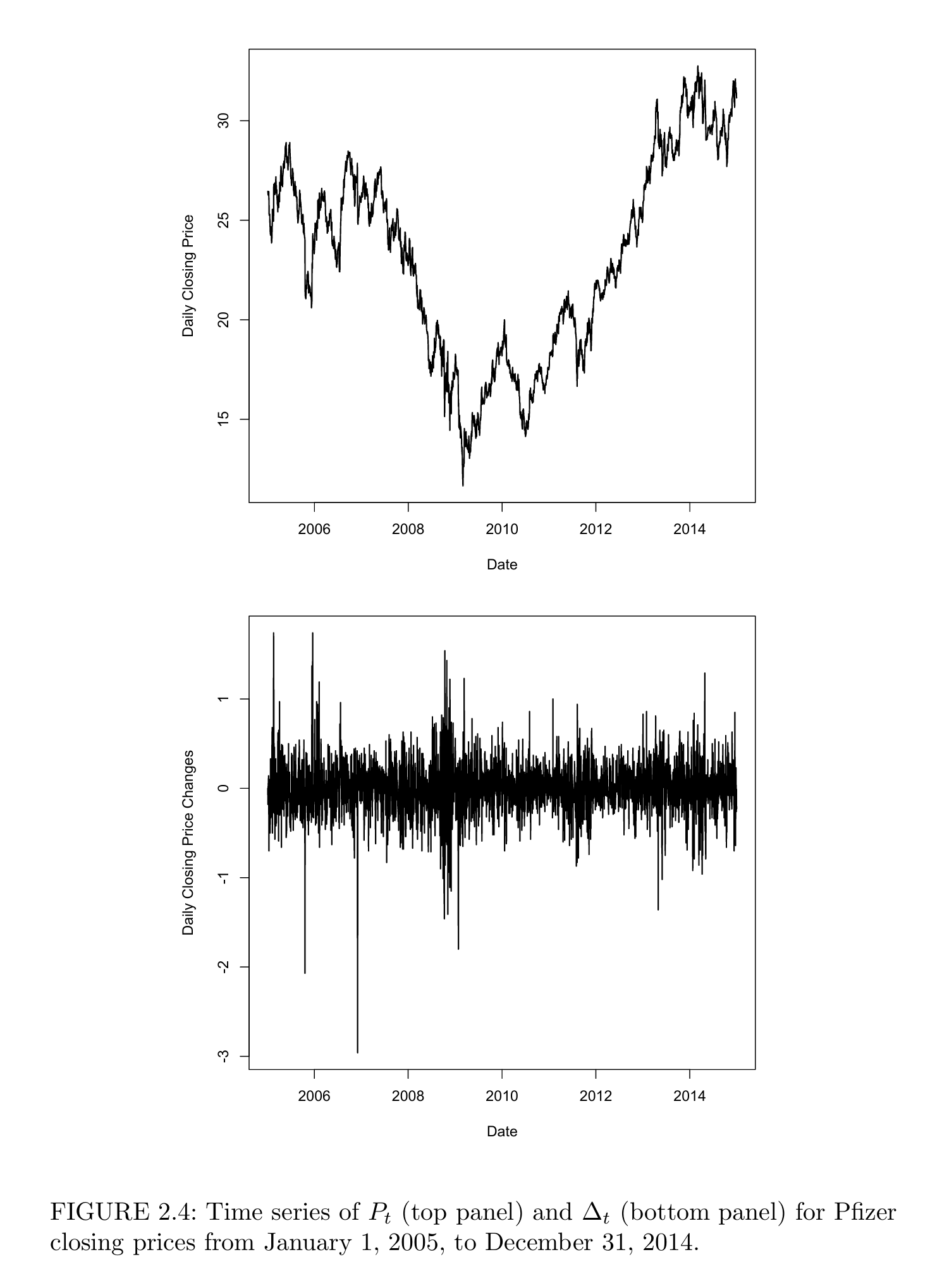
图2 股票每日收盘价和每日收盘价变化
《数理金融学》明确指出:图2所示的股票价格Pt和股票价格变化Dt均为时间序列(Time series),也就是说,股票价格Pt和股票价格变化Dt均为时间函数,因此,Dt就是《随机信号分析》中的白噪声信号n(t)。
但是,《数理金融学》的奠基人、法国数学家巴舍利耶(Bachelier)却将股票价格的变化Dt假设为独立同分布的“随机变量”,因而得出了股票价格Pt服从正态分布的结论:
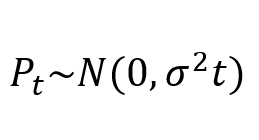
从而将股票价格Pt从“时间序列(时间函数)”改变为概念不同的“随机变量”。
显然,巴舍利耶在推导过程中,没有保持股票价格Pt和股票价格变化Dt概念的同一,将股票价格Pt和股票价格变化Dt从“时间序列(时间函数)”替换为“随机变量”,从而产生了违反同一律的“偷换概念”逻辑错误,这将导致Pt无法正确描述股票价格现象及规律。
例如,图2所示的股票价格Pt并不具有正态分布的“集中性”和“对称性”特征,Pt不可能服从正态分布。另外,巴舍利耶认为股票价格Pt随机波动的方差与时间t成正比,表明Pt随机波动的幅度随时间越来越大,但是,图2股票价格随机变化Dt的方差是固定的,与巴舍利耶的结论相悖。
《数理金融数学》基于巴舍利耶“股票价格服从正态分布”的结论,推导出了著名的B-S期权定价公式,由于无法正确描述并预测金融市场的波动趋势及波动程度,导致B-S期权定价公式成为造成1987、1997和2007年三次重大金融危机的罪魁祸首。
被誉为“中国金融数学开创者”的彭实戈院士在《中国基础研究发展报告(2019年)》中明确指出:B-S期权定价公式是造成以前历次重大金融危机的关键性原因。
畅销书《黑天鹅》作者塔勒布(Taleb)在《金融时报》上发表了题为“破坏市场的伪科学”专栏文章,对《数理金融学》进行了严厉的批判。塔勒布在文章中指出:人们从一次又一次的金融危机中得出了“《数理金融学》的有效性与占星术一样不靠谱”的惨痛教训,并痛斥B-S期权定价公式获得诺贝尔奖不仅是对科学的侮辱,而且一直使金融体系面临崩溃的风险。
彭实戈院士认为:现有数学理论无法正确描述、解释并预测金融现象,其主要原因是:现代金融现象是非线性复杂现象,传统的《概率论》是线性理论,因而无法正确描述、解释并预测现代金融市场的资产价格波动现象。
因此,彭实戈院士亲自带领山东大学数学学院和金融研究院的团队,自1997年以来一直致力于探索和研究《非线性概率论》。2018年在教育部基础研究“珠峰计划”的支持下,山东大学成立了彭实戈院士任主任的教育部非线性期望前沿科学中心,试图攻克现有数学理论无法正确描述、解释并预测金融市场资产价格波动现象的世界难题。
三、结论
《数理金融学》若采用《随机信号分析》的“时间函数”研究方法来描述股票市场中的价格波动现象,则可正确描述、解释并预测股票价格波动现象及规律,解决现有数学理论无法正确描述、解释并预测金融市场资产价格波动现象的问题,并彻底消除《数理金融学》给金融市场带来的金融危机风险。
转载本文请联系原作者获取授权,同时请注明本文来自高宏科学网博客。
链接地址:https://wap.sciencenet.cn/blog-3418723-1507933.html?mobile=1
收藏

