第一性原理(First Principles)是一种基于事物本质规律进行推演的思维范式与方法体系,其核心在于从不可再简化的基础真理出发,通过逻辑推理构建知识体系。
早在2000多年前,亚里士多德就在他的《形而上学》中探讨了第一性原理,认为每个系统中都存在一个最基本命题或假设(如欧几里得几何中的公理),它不能被违背、删除或忽略,是决定事物最本质的不变法则。
所以,推翻一个结论,无需从结论入手,而是从它的隐含假设开始。如果根基的隐含假设不成立,则结论自然不成立。
一、随机试验是《随机过程》理论的逻辑出发点
《随机过程》是研究动态随机现象统计规律性的一门学科。要对随机现象的统计规律性进行研究,首先要对随机现象进行重复观察。
《随机过程》和《概率论》把对随机现象的观察称为随机试验,并把随机试验的每一种可能结果称为样本点,记为ω,把全体样本点的集合称为随机试验的样本空间,记为Ω。
图1为《随机过程》的理论演进过程,显然,随机试验是《随机过程》的最基本命题或基础真理。
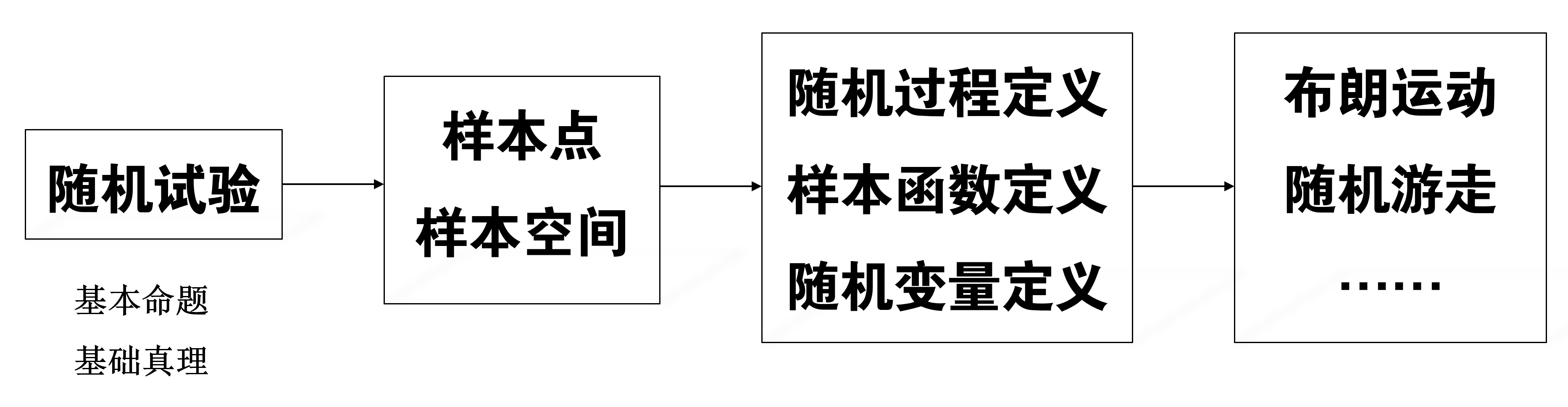
图1 《随机过程》理论的演进过程
二、随机过程、随机变量及样本函数定义
同时观察多个随机运动粒子的位移随时间变化过程,或多次观察一个随机运动粒子的位移随时间变化过程,可得到一族时间函数表示的随机试验结果(图2)。《随机过程》首先将随机试验的所有可能结果(一族时间函数)映射到样本空间Ω,每个时间函数对应一个样本点ω,然后用定义在Ω×T上的二元函数X(ω,t)来描述随机过程的所有试验结果。
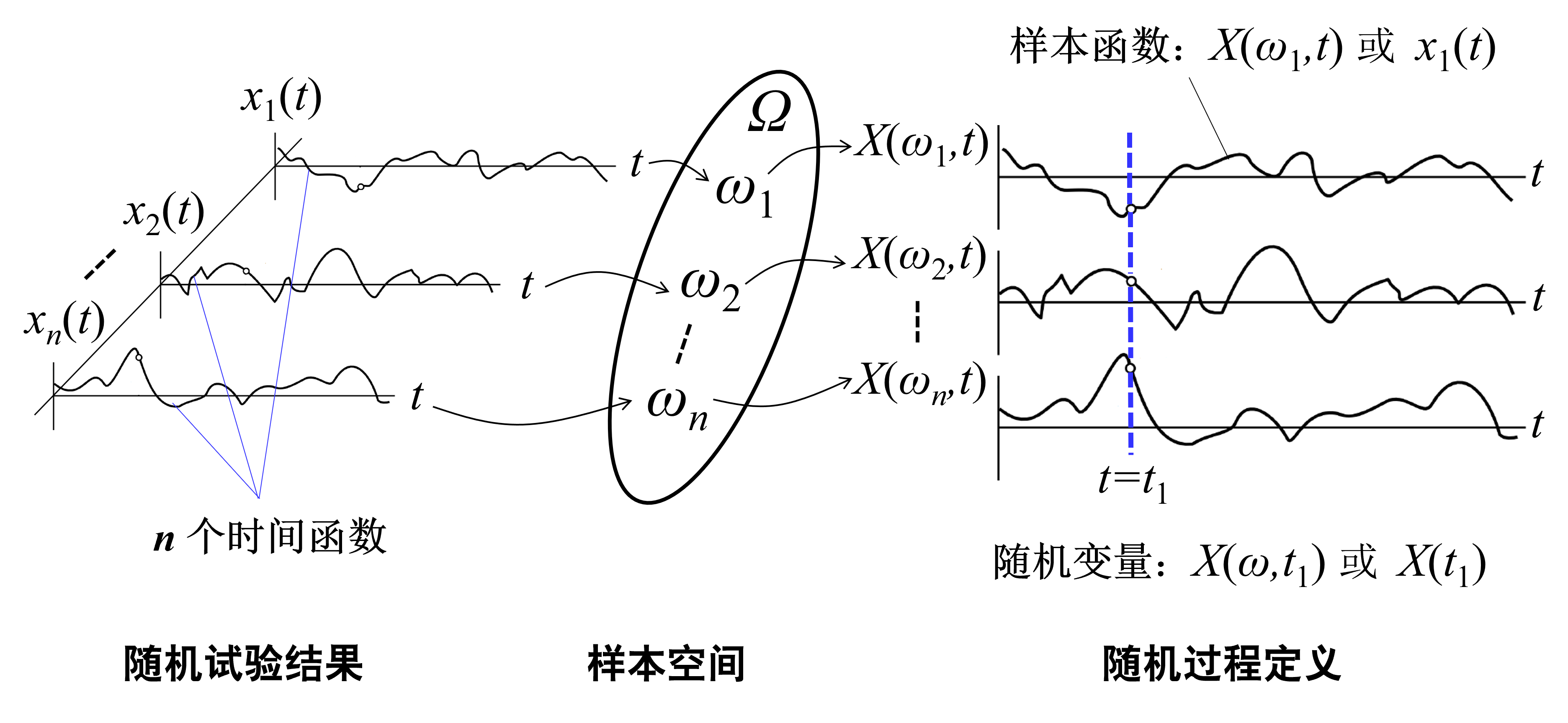
图2 随机过程、随机变量及样本函数定义
随机过程X(ω,t)有以下四种不同的情况:
(1)固定ω,X(ω,t)是时间t的函数,描述单个粒子的位移随时间变化过程,称为样本函数,或随机过程的一个物理实现,记为x(t)。
(2)固定t,X(ω,t)是样本点ω的函数,描述所有粒子在t时刻的空间位置分布状态,称为随机变量,记为X(t)。
注意:随机变量X(t)虽然使用了时间函数符号,但它不是时间t的函数,而是样本点ω的函数。
(3)固定ω,固定t,X(ω,t)是一个实数,表示某个粒子在t时刻的位移观测值。
(4)当ω和t同时变化时,X(ω,t)是一族依赖于样本空间的时间函数集合,或一族依赖于时间的随机变量集合,称为随机过程。
从随机过程X(ω,t)的定义可以看出,样本函数x(t)是描述单个粒子“个体行为”的数学概念,而随机变量X(t)是描述所有粒子“集体行为”的数学概念。
三、《随机过程》“混淆概念”逻辑错误分析
从图2所示的随机试验结果和随机过程定义可以看出,《随机过程》的研究对象有两个:
一是单个粒子的运动状态(位移、速度及加速度)随时间t的变化过程,随机过程定义将单个粒子在t时刻的位移x(t)抽象为样本函数x(t);
二是所有粒子在t时刻的空间位置分布状态,随机过程定义将所有粒子在t时刻的空间位置[x1(t), x2(t),……, xn(t)]抽象为随机变量X(t)。
表1 为《随机过程》的随机过程定义和布朗运动定义对两个研究对象的数学抽象。
表1 《随机过程》研究对象及数学抽象

从表1可以看出,随机过程定义将随机试验中的单个粒子在t时刻的位移x(t)抽象为样本函数x(t),而布朗运动定义却将随机试验中的单个粒子在t时刻的位移x(t)抽象为随机变量X(t)。
显然,布朗运动定义没有保持与随机过程定义概念的一致性,将“随机变量”和“样本函数”这两个内涵与外延完全不同的数学概念等同使用,产生了违反同一律的“混淆概念”逻辑错误。
布朗运动定义的“混淆概念”逻辑错误不仅使《随机过程》教科书在逻辑上不能自洽,而且导致《随机过程》教科书对布朗运动位移和瞬时速度的描述与自然科学、工程技术和社会科学大量的观察实验结果不符,无法正确描述实际的布朗运动现象及规律。
四、数学史上最著名的“混淆概念”逻辑错误
数学史上最著名的违反同一律“混淆概念”逻辑错误出现在牛顿创立的《微积分》理论中。
牛顿首先假设质点位移x(t)的增量∆x≠0,然后在推理和证明过程中又随意令∆x=0,将两个完全不同的数学概念等同使用,产生了著名的“贝克莱悖论”,从而引发了一场持续150多年的“第二次数学危机”,《微积分》理论险被推翻。
英国大主教贝克莱(Berkeley)严厉批评牛顿是有意识地“混淆概念”,《微积分》理论是“分明的诡辩”,并指出“逻辑错误不会产生科学”。
法国著名数学家罗尔(Rolle)则批评牛顿的《微积分》完全基于不严谨的逻辑推理,认为“微积分是巧妙的谬论的汇集”。
整个18世纪,数学家们的首要任务就是消除《微积分》中违反同一律的“混淆概念”逻辑错误,几乎每一位数学家都为此做出了巨大的努力。
后来柯西(Cauchy)将极限概念作为《微积分》的理论基础,才彻底消除了牛顿《微积分》中的“混淆概念”逻辑错误和“贝克莱悖论”,彻底解除了数学史上的第二次危机。
五、结论
历史总是惊人的相似,还是那熟悉的姿势,《随机过程》如今也步牛顿《微积分》的后尘,出现了违反同一律的“混淆概念”逻辑错误,这将导致《随机过程》理论面临重大范式危机和范式转换,为中国的数学学科进入世界一流水平前列提供了千载难逢的历史性发展机遇。
转载本文请联系原作者获取授权,同时请注明本文来自高宏科学网博客。
链接地址:https://wap.sciencenet.cn/blog-3418723-1498105.html?mobile=1
收藏

