 精选
精选
近年来的人工智能发展,从总体上看,是不太介意有没有可解释性的,预测性能为王,因为后者更容易变现。
自留地—随机邻域嵌入
事情得从t-sne(t分布的随机邻域嵌入, t-stochastic neighborhood embedding)说起,深度学习研究者都希望通过可视化的方法来让人们看到模型到底干什么,以便能更好地说明模型的效果,顺便通过可视化的图把论文的页数填满。
对于预测或者分类问题,t-sne能够比较好地在二维平面上将不同类别的数据点用不同颜色着色后展示出来。如果分得好,那么相同类别的数据点会聚在一起,且与其它类别分得比较开,就像一块一块自留地一样。他意味着,只要用几个简单的线性分类器,比如建几条直路,就能把各自的自留地分开,从而大幅度减少分割不好引发的土地纠纷。分得不好,那不同类别的数据就会像打群架一起,混在一起,傻傻分不清楚。
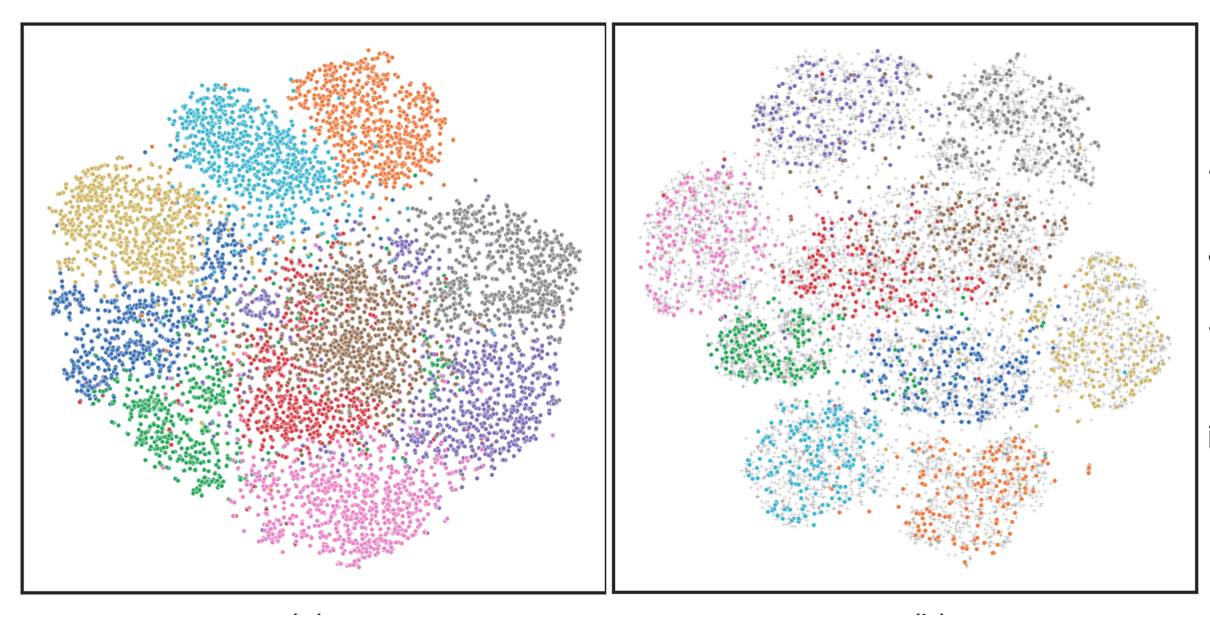
图1: t-sne数据可视化示例
t-sne的发布时间算起来其实也不短,距今快20年,是由深度网络先驱兼大咖辛顿提出的。这一算法提出的大背景是当时风头正盛的流形学习(manifold learning)。一开始是2000年三篇代表作的出现,一篇是强调人类认知可能是以连续吸引子而非我们常见的离散吸引子来记忆事物,比如人的身份。连续的好处在于允许只记一张人脸,却可以在大脑里张成一条曲线或一个曲面甚至更高维的超曲面,那么当再次碰到同一人,但不同角度时,人们可以在这隐含了角度控制变量的超曲面上自由旋转来匹配相同人的身份。另两篇则是用相对简单的算法发现高维数据里的低维结构,如从手旋杯数据中发现了内在的旋转,从人脸数据集发现了上仰下俯、左右变换甚至表情的低维表达。因为从理论上,超曲面是流形的一种表达形式,从认知上,他又能解释一些现象,从维度上,他又实现了高维数据的降维并能可视化进行解释。所以,这三篇代表作迅速地掀起流形学习研究的热潮。
辛顿也不例外。他首先提了一个随机邻域嵌入算法。这个算法的特点是假设高维数据是存在分布的,但分布在邻域意义下是不对称的,比如我自留地和其它相邻的几块包括张三的可以形成一个分布。张三的也可以和其它人的形成分布。这样的话,以我为中心张三的自然地出现的概率,就不会等同于张三为中心我的自由地出现的概率,因为我和张三划邻域的框是不同的。这文章发表后不久,辛顿又发现一个问题,高维数据在低维可视化时,如果数据真正的低维是十维,硬坍缩到二维来显示,有可能会把数据点原本正常的结构也压缩点,毕竟居住面积减少太多了。所以,他把不对称的概率分布用t-分布做了替换,从而解决了这一问题。他也把t-sne的源码开了源。至此,人工智能的科研工作者们都乐得使用t-sne来了解自己提的算法是否能够把数据点分开,以便验证算法的预测性能是好是坏。虽然后来有t-sne可视化改到三维球上显示的,也有其他一些改进,但t-sne仍然稳定下来,成为人工智能领域首选的高维数据可视化工具。
一分为二 -- 线性判别分析
为啥经t-sne可视化后,数据分得越开,就能叫好呢?这事倒不是t-sne提出的,是更早的线性判别分析(Linear Discriminant Analysis, 简称LDA)形成的观念。t-sne只是负责可视化。
最早这么思考的方法是线性判别分析,而在此之间科学家们常用的数据降维方法是主成分分析(Principal Component Analysis,简称PCA)。自1904年左右提出至今,它统治了数据分析领域可能近百年时间。从名字可以知道,主成分分析希望做的是发现主要矛盾,去掉次要矛盾。从统计的角度来看,比如第一主要矛盾,就是找一条穿过数据中间的步道。这条道最能反映沿数据跑直线时,能展开的最大长度,同时,又能保证数据点到这条步道的距离差的总和最小。严格来说,即是保持方差(长度)最大,偏差(距离差)最小。第二主要矛盾找法相同,只是道路与第一主要矛盾的垂直。通过找与前几主要矛盾垂直的步道,最终能找到若干能代表数据主要矛盾的步道,俗称主成分。
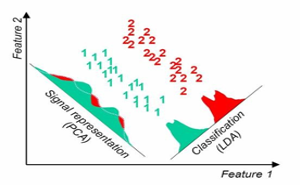
图2: 主成分分析(PCA)与线性判别分析(LDA)对数字1和2的降维可视化效果
不过,主成分的问题在于没有利用数据点的标签,比如人脸图像数据,张三照片的标签是张三,李四的标签是李四。如果想做好人脸识别,提升识别性能,只找到主要矛盾的帮助不大,更好的策略是利用标签。如何用呢?一个直接的思路,是让同一标签的都尽可能靠在一起,比如张三在不同时间、不同角度拍的照片聚在一起,再让不同标签的都尽量分开,比如张三的照片放一团,李四的也放一团。在这种情况下,我要找条能把这两人分开的路,便是第一判别主要矛盾。而要获得这条路的办法,是保证类内尽可能小,类间尽可能大。直觉来想,要实现这个目标,极端情况下,就是要把同一类的缩成一个点,不同类的拉远即可。这便促成了线性判别分析的算法动机。借助这一思路,引入标签的学习策略都能很大程度地提升了预测的性能。即使到了人工智能的深度学习时代,为了提升预测性能,采用的策略依然如此。一方面尽可能多的加标签,监督学习是人工加标签、自监督学习是利用数据特点来生成正负标签、基于人类反馈的强化学习是学习人类的标签,诸如此类;另一方面则是沿袭线性判别分析的观念,比如深度学习里常用的两个损失函数:对比损失和三元组损失函数,从其机理来看,仍然是期望获得“类内足够小,类间足够大”。
退化的结构/可解释性
值得我们注意的是,主成分分析与线性判别分析之间的差异在于前面捕捉了数据的统计结构。与主成分分析类似的保持结构的还有不少,比如上面提及的流形学习,是为了保持数据的几何结构,使其尽可能光滑。反观从预测角度出发的线性判别分析,并不关心结构的保持,而是为了能让标签的预测尽可能准确,有意识的坍缩类内空间和拉远类间距离。从近几年来的深度学习文章来看,用t-sne可视化特征表达时,似乎都在表达这层意思。同类数据成团了,不同类的有了好的分离。虽然也有如解耦学习这样的,期望把某些维度拉伸获得一定的可解释性,但既然主要目标是提升预测,其它维度必然会被牺牲不少。
然而,结构的丢失,或多或少意味着数据原本结构的丢失,这意味着可解释性的丢失。
而这种结构或可解释性的保持或恢复,也许才是人工智能打开人类智能之门的关键钥匙。
张军平
2024年4月15日
转载本文请联系原作者获取授权,同时请注明本文来自张军平科学网博客。
链接地址:https://wap.sciencenet.cn/blog-3389532-1429859.html?mobile=1
收藏

