引用本文
程松松, 陈茹, 樊渊, 邱剑彬. 基于镜像下降的分布式弱凸优化算法研究. 自动化学报, 2025, 51(8): 1842−1856 doi: 10.16383/j.aas.c240784
Cheng Song-Song, Chen Ru, Fan Yuan, Qiu Jian-Bin. Distributed mirror descent algorithm design for weakly convex optimization. Acta Automatica Sinica, 2025, 51(8): 1842−1856 doi: 10.16383/j.aas.c240784
http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c240784
关键词
分布式优化,弱凸,镜像下降,Bregman-Moreau包络,零阶梯度
摘要
机器学习中的诸多非凸优化问题, 如鲁棒相位恢复、低秩矩阵补全以及稀疏字典学习等, 本质上可归结为弱凸优化问题. 然而, 弱凸优化问题固有的非凸特性使得此类问题的求解极具挑战. 此外, 由于系统复杂度和问题规模的增加以及相关参数的分布式存储需求, 传统的基于单个个体的集中式计算框架难以高效求解此类问题. 针对上述挑战, 设计一种分布式镜像下降算法, 并从Bregman-Moreau包络的角度分析其收敛性, 证明算法的收敛速度为$ \mathrm{O}(\ln K/\sqrt{K}) $, 其中$K$为算法的迭代步数. 进一步地, 考虑目标函数梯度信息难以精确获取的情形, 采用正交随机方向矩阵法进行梯度估计. 相较于传统的基于随机向量的方法, 该方法利用多维方向信息进行估计, 从而显著提高梯度信息的估计精度和效率. 基于高效的梯度信息估计, 提出一种分布式零阶镜像下降算法, 并获得与已知精确梯度信息情形下相一致的收敛速度. 最后, 通过基于相位恢复问题的数值仿真和实验验证了所提出的两种算法的有效性.
文章导读
现实世界中, 很多问题都可以转化为优化问题来解决, 如基于传感器网络的定位问题、智能电网的资源分配问题以及推荐系统的设计问题等. 然而, 随着问题规模和复杂度的增加, 传统的集中式框架难以实现大规模复杂优化问题的求解. 基于网络化系统的分布式优化因其鲁棒性强、隐私性好以及不依赖中心节点等优点能够有效求解大规模优化问题[1−7]. 针对基于网络化系统的大规模优化问题, 涌现了诸多性能优良的分布式求解算法[8−11].
在实际场景中, 个体的决策变量往往受资源的限制, 相应的问题通常构建成带有集合约束的分布式优化问题. 针对有集合约束的凸优化问题, 文献[12]设计基于投影的分布式算法, 并分析算法的收敛性能. 文献[13]则研究集合约束下的分布式光滑凸优化问题, 从原始−对偶的角度设计基于投影的分布式比例−积分算法. 文献[14]考虑多个集合约束的分布式强凸优化问题, 指出多个集合约束情形下带有固定步长的投影梯度跟踪算法的非精确收敛性, 并通过设计衰减步长保证算法的收敛性. 但是上述算法在确定具体的投影点时基本都是基于欧氏距离框架进行计算. 这种基于欧氏距离的投影方法理论简单、便于分析, 但通常仅适用于处理简单的集合约束, 针对较复杂的约束集合(如单纯形等), 难以给出投影点的显示表达. 镜像下降(Mirror descent)采用Bregman散度替代传统欧氏距离度量, 是一种基于对偶域优化的参数学习算法, 该类算法能够有效地处理带有复杂约束集合的优化问题. 针对凸优化问题, 文献[15]提出一种镜像下降算法, 指出该算法是投影次梯度算法的一般推广, 特别地, 当距离生成函数为欧氏二范数时, 则退化为投影次梯度算法. 针对有约束的随机凸优化问题, 文献[16]设计分布式镜像下降算法, 并结合Epoch技术进一步优化算法的收敛性能.
在现实工程应用中, 很多分布式优化问题在本质上是非凸的(目标函数为非凸函数或可行域为非凸集合). 然而, 由于非凸优化问题的种类繁多, 目前尚缺乏统一的分布式求解算法, 并且现有算法的收敛性能往往不甚理想. 例如, 针对特定类型的非凸优化问题, 文献[17]设计依赖中心节点的近端交替方向乘子法(Proximal alternating direction method of multiplier, P-ADMM), 但该方法仅能渐近收敛到算法稳定点的邻域. 值得注意的是, 现实中很多非凸优化问题, 例如鲁棒相位恢复、低秩矩阵补全和稀疏字典学习, 可以等效转化为弱凸优化模型, 以便更有效地求解. 针对可行集约束下的弱凸优化问题, 文献[18]提出一种基于动量的Frank-Wolfe算法, 但其收敛速度仅局限于$ \mathrm{O}(1/\ln K) $. 文献[19]首次设计投影次梯度方法, 并从Moreau包络的角度证明了算法能够以$ \mathrm{O}(\ln K/\sqrt{K}) $的速度收敛到最优解. 进一步地, 文献[20]将次梯度方法推广到有通信延迟的情形, 并证明了在弱凸目标函数满足锐度特性的条件下, 该方法具有线性收敛速度.
目标函数的梯度信息在设计优化算法时直接影响算法的迭代方向. 然而在很多实际问题中, 目标函数的梯度信息往往难以甚至无法精确获取. 为此, 一种可行的策略是在决策变量邻域进行微小摄动, 并利用摄动点和原决策变量点的目标函数值进行差分, 从而估计梯度信息. 针对凸优化问题, 文献[21]从双向差分、左向差分以及右向差分三个维度提出梯度信息的估计策略, 并在此基础上设计分布式优化算法. 此外, 文献[22−23]研究分布式随机零阶梯度算法. 针对分布式非凸优化问题, 文献[24]从原始−对偶的角度设计分布式零阶优化算法, 并证明了其在PŁ 条件下的线性收敛性. 而文献[25]则进一步将零阶梯度与梯度跟踪技术相结合, 提出一种新的分布式优化算法, 并系统地论证了其在满足PŁ 条件下的线性收敛性.
基于以上讨论, 分布式有约束弱凸优化的求解尚存在如下问题有待进一步解决:
1) 针对带有简单约束的弱凸优化问题, 可采用传统的投影梯度方法进行求解. 然而针对带有复杂约束的弱凸优化问题, 投影梯度方法在保证解的可行性时计算负担较大. 如何设计更有效的分布式镜像下降算法求解该类问题?
2) 针对有约束弱凸优化问题, 现有的基于投影梯度方法构建的Moreau包络分析框架难以直接应用于分布式镜像下降算法的收敛性能分析. 如何拓展现有Moreau包络框架以分析分布式镜像下降算法的收敛性?
3) 在梯度信息不可精确获取的情形下, 如何突破现有梯度估计框架, 设计更高效的梯度估计策略, 以提升算法的求解性能? 此外, 基于零阶梯度设计的算法能否获得和基于精确梯度信息算法相匹配的收敛性能?
针对上述挑战, 本文聚焦于大规模有约束弱凸优化问题, 设计分布式镜像下降算法, 并进一步扩展至梯度信息不可精确获取的情形, 分析算法收敛性能, 并应用于相位恢复问题的求解. 本文的主要贡献简要总结如下:
1) 相较于文献[12, 19]中基于欧氏距离的投影算法, 本文设计更一般的基于Bregman散度的镜像下降算法, 能够有效处理更复杂的集合约束(如单纯形约束等). 此外, 与文献[15−16]中针对强凸函数的镜像下降算法相比, 本文考虑更一般的弱凸优化问题, 从而拓宽了镜像下降算法的适用范围.
2) 针对分布式弱凸优化问题的非凸属性, 本文从Bregman-Moreau包络的角度建立算法收敛性能的分析框架, 并从邻近投影的角度分析算法的收敛速度. 特别地, 文献[19, 26]中的相关方法和结果即为本文中距离生成函数$ \phi({{{\boldsymbol{x}}}}) $取$ \frac{1}{2}\|{{{\boldsymbol{x}}}}\|^{2} $时的特殊情况.
3) 相较于传统的基于随机向量的梯度估计策略[21−25], 本文从更高维度引入基于随机方向矩阵的梯度信息估计方法, 提升梯度信息的估计精度. 在此基础上, 本文设计分布式零阶优化算法, 并证明其收敛速度可达到$ \mathrm{O}(\ln K/\sqrt{K}) $.
本文结构安排如下: 第1节介绍网络拓扑相关的基础知识并给出分布式弱凸优化问题以及相关的基础理论; 第2节考虑在梯度信息精确已知的情形下, 设计分布式镜像下降算法, 并分析算法的收敛性能; 第3节进一步考虑梯度信息未知情形, 设计基于零阶梯度的分布式镜像下降算法并给出算法收敛性能; 第4节通过相位恢复的数值仿真和实验验证了所提算法的有效性; 第5节总结全文.
图 1 网络化系统示意图
图 2 例1中算法1和算法2的仿真结果
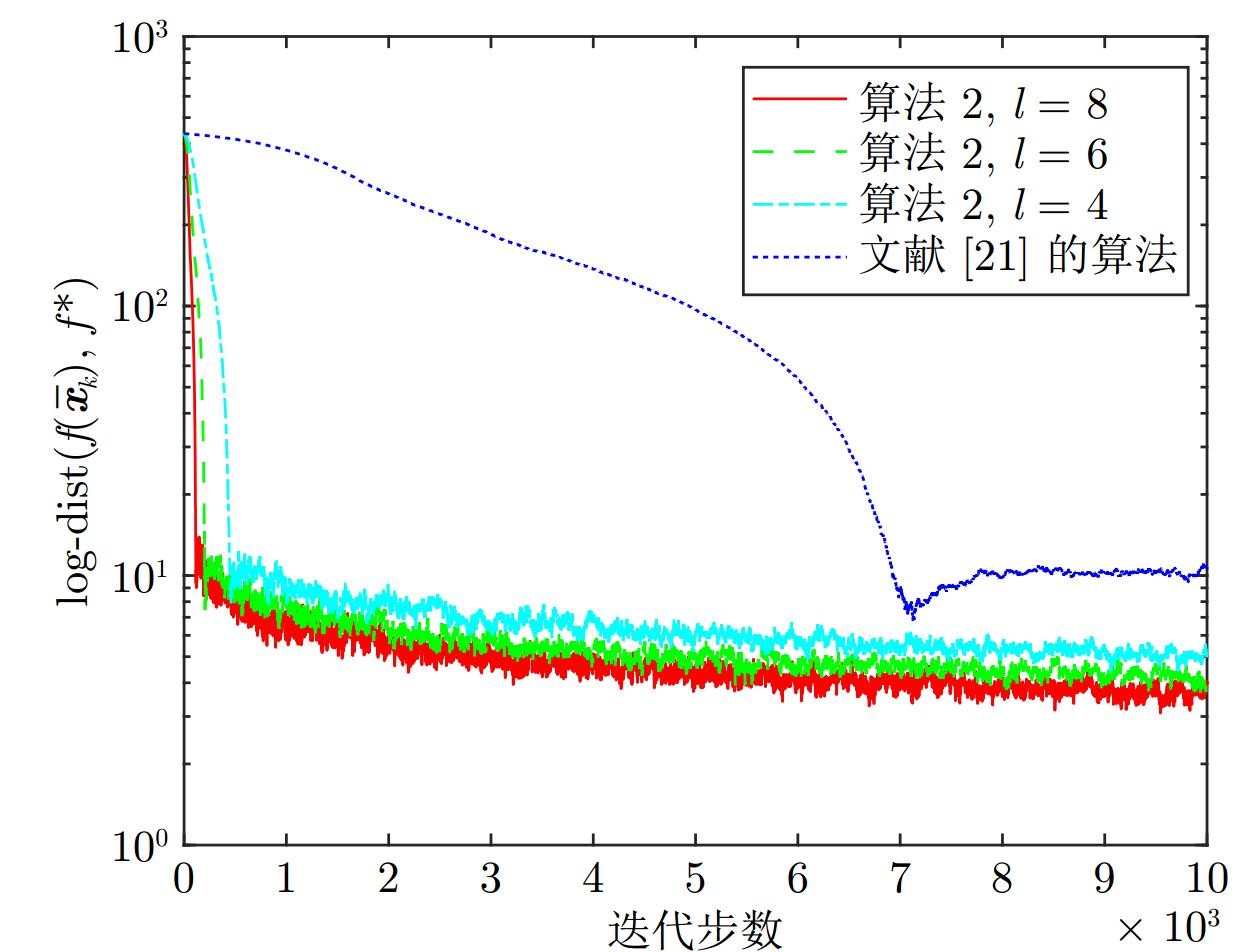
图 3 例1中算法2与文献[21]中算法的仿真结果
针对广泛存在的大规模弱凸优化问题, 本文设计分布式镜像下降算法, 从Bregman-Moreau包络的角度分析算法的收敛性. 此外, 考虑梯度信息无法精确获取, 提出基于正交随机方向矩阵的分布式零阶镜像下降算法. 特别地, 正交随机方向矩阵列数$ l $越大, 梯度信息估计效果和算法收敛性能越好. 经分析, 本文所提出的一阶和零阶分布式镜像下降算法均能获得$ \mathrm{O}(\ln K/\sqrt{K}) $的收敛速度.
作者简介
程松松
安徽大学电气工程与自动化学院副教授. 2018年获得中国科学技术大学控制科学与工程专业博士学位. 主要研究方向为分布式计算, 优化与博弈. E-mail: sscheng@ahu.edu.cn
陈茹
安徽大学电气工程与自动化学院硕士研究生. 主要研究方向为基于对偶理论的分布式非凸优化与博弈. E-mail: ruchen@stu.ahu.edu.cn
樊渊
安徽大学电气工程与自动化学院教授. 2011年获得中国科学技术大学和香港城市大学控制科学与工程专业博士学位. 主要研究方向为分布式控制与优化, 机器人导航与控制. 本文通信作者. E-mail: yuanf@ahu.edu.cn
邱剑彬
哈尔滨工业大学智能控制与系统研究所教授. 2009年获得中国科学技术大学和香港城市大学机械电子工程专业博士学位. 主要研究方向为智能控制理论与应用, 人工智能大模型, 航天器智能自主控制, 智能机器人. E-mail: jbqiu@hit.edu.cn
转载本文请联系原作者获取授权,同时请注明本文来自Ouariel科学网博客。
链接地址:https://wap.sciencenet.cn/blog-3291369-1504549.html?mobile=1
收藏