科学网-基于边缘动态事件触发的在线分布式复合Bandit优化算法-Ouariel的博文

基于边缘动态事件触发的在线分布式复合Bandit优化算法

2025-9-30 15:33

阅读：1416

引用本文

熊梦辉, 杨春雨, 赵建国, 张保勇, 袁德明. 基于边缘动态事件触发的在线分布式复合Bandit优化算法. 自动化学报, 2025, 51(8): 1811−1828 doi: 10.16383/j.aas.c250070

Xiong Meng-Hui, Yang Chun-Yu, Zhao Jian-Guo, Zhang Bao-Yong, Yuan De-Ming. Edge dynamic event-triggered-based online distributed composite Bandit optimization algorithm. Acta Automatica Sinica, 2025, 51(8): 1811−1828 doi: 10.16383/j.aas.c250070

http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c250070

关键词

在线分布式优化，复合优化，动态事件触发通信，Bandit反馈，动态遗憾

摘要

研究带宽受限的非平衡有向多智能体网络环境下的在线分布式复合Bandit优化问题. 该问题中每个智能体的局部目标函数具有复合结构: 其一为梯度信息不可获取的时变损失函数, 其二为具有特定结构的正则化项. 为应对网络带宽的受限, 设计具有控制因子的边缘动态事件触发通信协议, 以降低通信开销. 同时, 针对局部损失函数梯度信息难以获取的挑战, 分别引入单点和两点梯度估计方法, 以支撑损失函数梯度信息的获取. 基于此, 结合近端算子, 分别设计仅要求加权邻接矩阵满足行随机性质的在线分布式复合单点和两点Bandit优化算法, 并使用动态遗憾指标分析两种算法的收敛性. 结果表明, 在合理的假设和参数设定下, 两种算法在期望意义下分别可获得${\cal{O}}({K^\frac{3}{4}}(1+{{\cal{P}}_K}))$和${\cal{O}}({K^\frac{1}{2}}(1+{{\cal{P}}_K}))$的动态遗憾上界, 其中$K$是总迭代次数, ${\cal{P}}_K$是路径变差度量. 进一步, 当${\cal{P}}_K$能够被提前估计时, 两种算法分别可获得${\cal{O}}({K^\frac{3}{4}}\sqrt{1+{{\cal{P}}_K}})$和${\cal{O}}({K^\frac{1}{2}}\sqrt{1+{{\cal{P}}_K}})$的期望动态遗憾上界. 最后, 通过对在线分布式岭回归问题的仿真实验, 验证了算法的收敛性以及理论结果的正确性.

文章导读

近年来, 随着机器人技术、人工智能、无线通信及计算机科学等领域的迅猛发展, 控制系统的规模不断扩大, 控制任务的复杂性也日益增加, 从而推动多智能体系统的快速发展. 多智能体系统是由一群具备一定感知、通信、计算和执行能力的智能体通过特定方式相互关联而构成的大规模网络系统, 其优势在于通过智能体之间的信息交互与协同合作, 能够有效地完成某些特定的复杂任务[1−2]. 分布式优化是在多智能体系统的框架下, 通过智能体之间的协作和交互来实现全局优化目标. 与传统的集中式优化不同, 分布式优化是一种去中心化的优化方式, 其不依赖一对一的全局通信, 而仅要求相邻智能体之间进行局部信息交换. 这种“分而治之”的特性, 使得分布式优化在应对大规模复杂问题时, 展现出较高的灵活性和鲁棒性, 因而被广泛应用于电力系统、机器学习、传感器网络等领域[3−6], 并得到越来越多的关注.

在分布式优化框架的初期构建阶段[7], 主流的分布式优化算法主要是以离线形式呈现, 如(投影)梯度下降算法、对偶平均算法、镜面下降算法等[8−11]. 更多详细介绍可参见相关综述[12−14]. 这些算法主要适用于静态环境中的优化问题, 即目标函数在整个迭代过程中保持恒定不变. 然而, 在实际应用中, 许多优化问题往往处于动态或不确定环境中, 目标函数可能随时间发生变化. 在这种情况下, 在线优化架构应运而生[15]. 该架构可视为在线参与者(玩家)与对手(环境)之间的一个有结构、反复进行的博弈过程, 具体规则如下: 在初始迭代时刻, 在线参与者做出决策, 该决策对应一个代价, 而该代价在决策前无法预知, 仅能在做出决策后由对手揭示. 在线参与者根据所揭示的代价信息(梯度或相关函数值), 更新下一迭代时刻的决策, 从而生成一系列决策, 以最小化累积代价函数[16]. 与离线分布式优化不同, 基于在线优化架构的在线分布式优化能够适应复杂且实时变化的动态环境, 允许目标函数在迭代过程中动态变化. 这使得其能有效应对具有任务时变、环境突变等挑战性的应用场景[17−19]. 进一步地, 在在线分布式优化场景中, 一些优化问题可能同时涉及时变目标函数以及具有其他复杂性质的函数(如非光滑的正则化项等), 从而衍生出在线分布式复合优化问题[20]. 机器学习中涉及$ L_1 $范数正则化项的LASSO (Least absolute shrinkage and selection operator)问题就是一个典型例子. 解决这类问题的相关算法包括在线分布式近端梯度下降算法[21−24]、在线分布式复合镜面下降算法[20]、分布式前向–后向分裂算法[25]等.

在一些在线分布式优化的真实应用场景中, 由于计算资源或其他不确定因素的限制, 导致直接获取目标函数的梯度信息是不现实的. 例如, 在数据网络的在线路由问题[16]中, 在线决策者从已知网络中选择一条路径(其代价是所选路径的长度)后, 其仅能测量一个数据包通过网络传输的往返时延, 而很难掌握整个网络的拥堵模式. 这个问题体现在线优化模型的一个典型挑战: 目标函数的梯度信息有时难以获取. 由于缺乏对网络全局状态的完全了解, 决策者只能基于有限的局部信息做出决策, 而无法直接依赖于整个系统的拥堵或延迟模式进行优化. 在这种情况下, 基于梯度信息的在线优化算法变得不再适用, 因此需采用一些无梯度在线优化算法来应对此类问题. 例如, 基于Bandit反馈的在线优化算法[26−27], 通过仅依赖在决策点附近的一个或多个目标函数值来进行梯度估计, 从而避免对全局梯度信息的需求, 有效解决了在信息不完全的环境下进行优化的挑战. 在已公开的关于在线分布式复合优化的研究[20−25]中, 文献[20, 23−24]均采用无梯度信息反馈的策略, 提出相应的算法框架. 具体来说, 文献[20]采用两点梯度估计方法, 设计基于两点Bandit反馈的在线分布式复合镜面下降算法; 文献[23]则分别采用单点和两点梯度估计法, 提出具有延迟Bandit反馈的在线分布式近端梯度下降算法; 而文献[24]则利用高斯平滑梯度估计方法, 在无梯度场景下设计基于事件触发的在线分布式近端梯度下降算法. 然而, 需要指出的是, 这些研究提出的算法框架通常要求通信网络是平衡的, 即通信网络所对应的加权邻接矩阵为双随机矩阵. 这一要求可能会给这些算法的实际应用带来一定的限制. 因此, 基于现有在线分布式复合优化算法框架, 深入探讨非平衡通信网络环境下的在线分布式复合Bandit优化算法具有重要意义. 这是本文的第一个研究动机.

在多智能体系统模型中, 智能体之间的通信交互通常依赖于通信网络. 然而, 在实际应用中, 通信网络的带宽资源往往是有限的. 因此, 在基于多智能体系统框架设计在线分布式(复合)优化算法时, 考虑网络带宽约束显得尤为重要. 在日趋成熟的网络化控制系统的研究中, 用于节约网络带宽资源的有效策略是事件触发通信[28−30]. 随着这一领域的不断发展, 事件触发通信的思想逐渐被引入在线分布式(复合)优化算法的研究中, 并且已经公开一些有意义的工作[24, 31−36], 其中仅有文献[24]针对在线分布式复合优化算法展开研究. 具体来说, 文献[24, 31−35]采用的事件触发通信协议均是基于节点形式, 即当特定节点触发事件时, 该节点将同步向其所有邻居传输信息. 这类事件触发通信协议虽然在一定程度上有助于节省网络带宽资源, 但在攻击频繁的开放网络环境中面临重大挑战, 甚至可能无法保证算法性能. 与此不同, 文献[36]采用边缘事件触发通信协议, 允许有选择性地异步传输信息, 从而能够更加灵活地应对网络环境的变化, 减少由于攻击或网络问题带来的潜在风险, 进而确保算法的性能. 此外, 值得指出的是, 上述文献中采用的事件触发通信协议本质上都是静态的, 即事件触发阈值通常是预先定义的单调非增函数. 这种设置在算法性能提升与带宽资源节约之间的权衡上可能存在一定的局限性. 因此, 在在线分布式复合Bandit优化算法的研究中, 设计一种合理的边缘动态事件触发通信协议显得尤为重要, 以便在保证算法良好性能的同时, 尽可能地节约网络带宽资源. 这是本文的第二个研究动机.

鉴于上述讨论, 本文首先设计一种带有控制因子的边缘动态事件触发通信协议. 然后, 结合近端算子, 运用单点和两点梯度估计方法, 在非平衡有向网络图上分别设计基于边缘动态事件触发通信的在线分布式复合单点和两点Bandit优化算法, 并在常规假设下分析两种算法的动态遗憾上界. 主要贡献如下:

1)考虑到基于多智能体网络的在线分布式复合Bandit优化问题中潜在的带宽资源受限, 设计一种带有控制因子的边缘动态事件触发通信协议, 以在保证算法性能的同时, 尽可能地节约网络资源. 不同于文献[24]采用的基于节点的静态事件触发协议, 我们所提出的事件触发协议是动态的、基于链接边的, 并且引入控制因子, 以更有效地节约网络资源. 与文献[37]针对连续时间优化算法设计的连续事件触发协议不同, 我们设计的是针对离散时间在线优化算法的离散边缘动态事件触发通信协议. 此外, 区别于文献[38]提出的基于节点的动态事件触发协议, 我们提出的动态事件触发协议是基于链接边的, 并且引入额外的控制因子.

2)我们移除在线分布式复合Bandit优化算法对双随机加权邻接矩阵的假设, 仅要求加权邻接矩阵满足行随机性质. 具体而言, 结合所提出的边缘动态事件触发通信协议和近端算子, 我们基于单点和两点梯度估计法, 在非平衡有向多智能体网络上分别开发具有边缘动态事件触发通信的在线分布式复合单点和两点Bandit优化算法, 能有效应对在线分布式复合优化问题中带宽受限以及损失函数梯度信息不易获取的挑战. 不同于文献[20, 23]开发的在线分布式复合Bandit优化算法, 我们所开发的算法不仅引入边缘动态事件触发通信协议以节约有限的网络资源, 还仅要求加权邻接矩阵满足行随机性质, 在一定程度上降低了算法的应用限制.

3)我们在合理的假设下分析两种算法的动态遗憾上界. 在常规的迭代步长设置下, 两种算法在期望意义下分别可获得$ {\cal{O}}({K^\frac{3}{4}}(1+{{\cal{P}}_K})) $和$ {\cal{O}}({K^\frac{1}{2}}(1\;+ {{\cal{P}}_K})) $的动态遗憾上界, 其中$ K $是总迭代次数, $ {\cal{P}}_K $是路径变差度量. 当$ {\cal{P}}_K $能够被提前预估, 并基于此设置迭代步长时, 两种算法在期望意义下可分别获得 $ {\cal{O}}({K^\frac{3}{4}}\sqrt{1+{{\cal{P}}_K}}) $和$ {\cal{O}}({K^\frac{1}{2}}\sqrt{1+{{\cal{P}}_K}}) $的动态遗憾上界.

本文其余部分安排如下: 第1节介绍本文所研究的优化问题模型及相关的预备知识; 第2节设计基于边缘动态事件触发通信的在线分布式复合单点Bandit优化算法, 并分析其动态遗憾上界; 第3节设计基于边缘动态事件触发通信的在线分布式复合两点Bandit优化算法, 并分析其动态遗憾上界; 第4节对比两种算法的动态遗憾上界; 第5节给出仿真实验; 第6节对全文进行总结与展望.

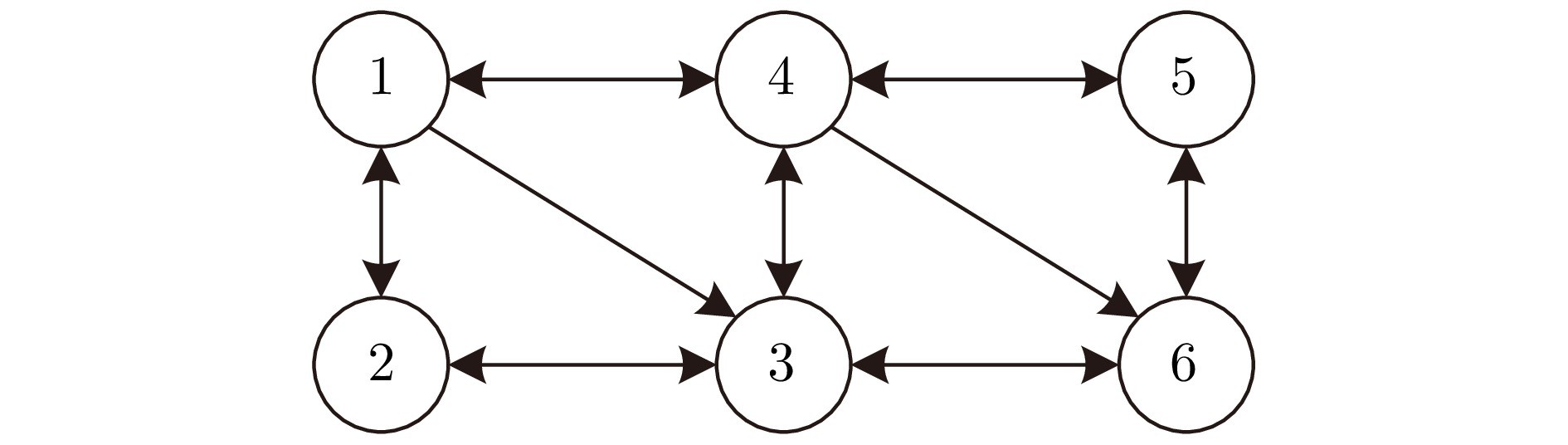
图 1 包含6个节点的有向网络图

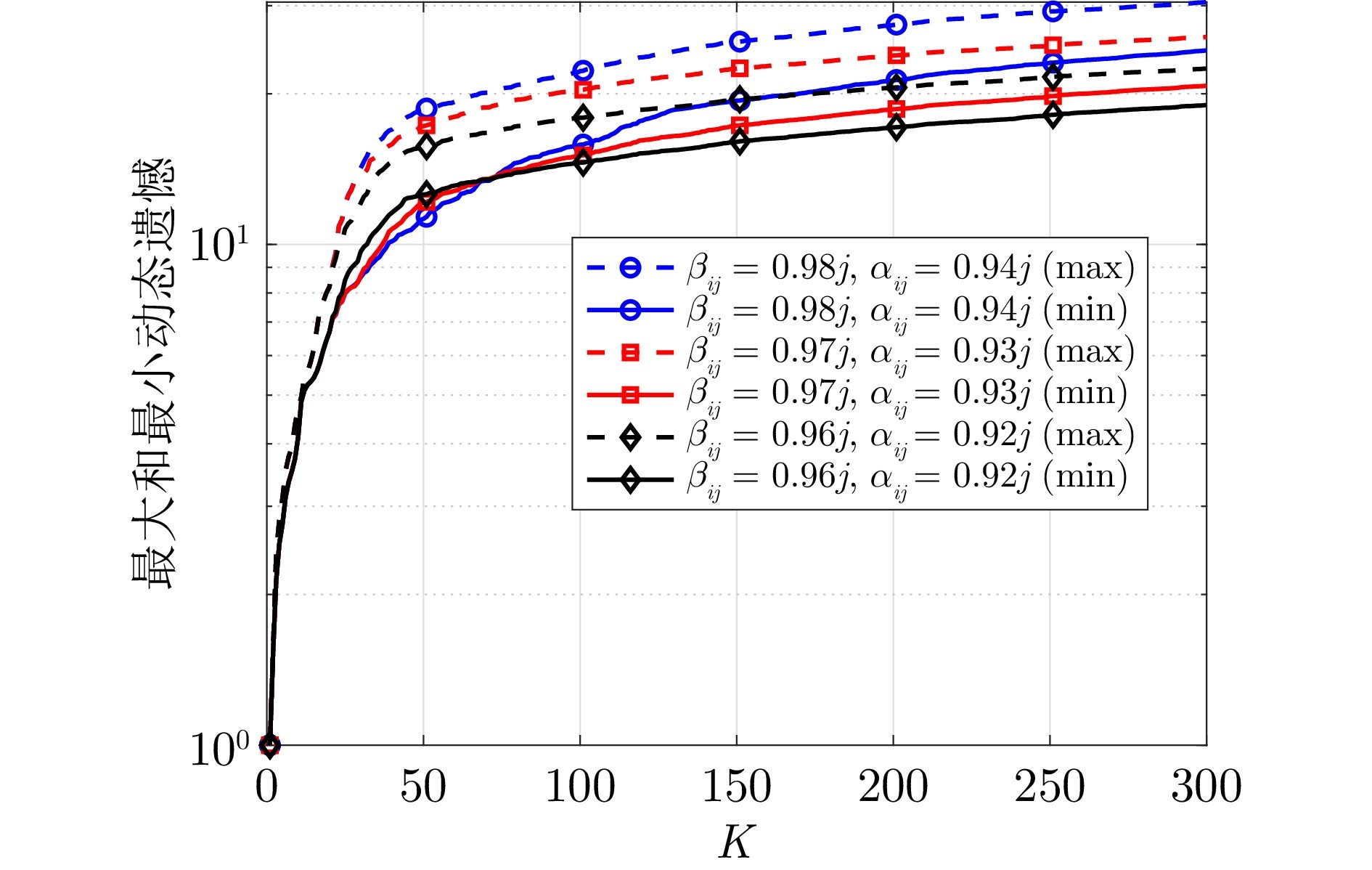
图 2 不同参数下算法1的动态遗憾($ j = 1,\;2,\; \cdots, \; 6 $)

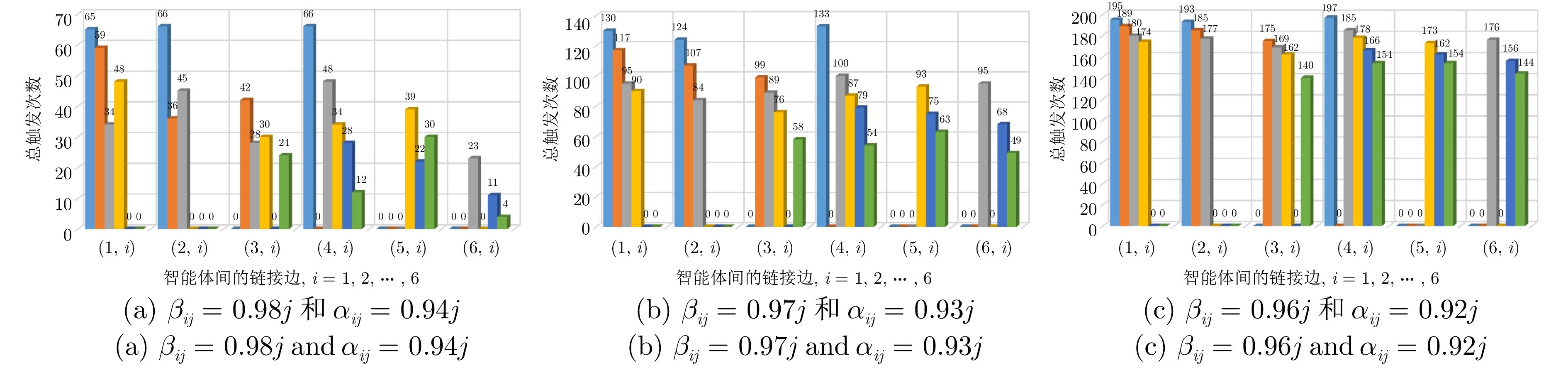
图 3 算法1下不同参数对应的链接边触发次数($ j = 1,\;2,\; \cdots, \; 6 $)

针对非平衡有向网络上的在线复合优化问题, 本文在局部损失函数梯度信息未知且网络通信带宽受限的双重考虑下, 分别基于单点和两点Bandit反馈策略, 提出两种具有边缘动态事件触发通信的在线分布式复合Bandit优化算法. 在合理的假设条件下, 采用动态遗憾指标理论分析两种算法的收敛性, 严格证明在适当参数配置下, 两种算法均能实现次线性的动态遗憾增长. 此外, 通过设置具体参数, 还明确给出两种算法动态遗憾增长速率的表达式. 最后, 以在线分布式岭回归问题为仿真算例, 验证了所提算法的有效性及理论结果的正确性, 同时揭示了事件触发参数对算法收敛性能的影响. 未来, 将算法从固定有向网络推广至时变有向网络, 并在触发协议中设计更为有效的自适应控制因子, 将是一个极具研究价值的方向.