引用本文
曹力丰, 阎高伟, 肖舒怡, 董珍柱, 董平. 基于域适应物理信息神经网络的时间序列预测方法. 自动化学报, 2025, 51(6): 1329−1346 doi: 10.16383/j.aas.c240566
Cao Li-Feng, Yan Gao-Wei, Xiao Shu-Yi, Dong Zhen-Zhu, Dong Ping. Time series prediction method based on domain adaptation physics-informed neural network. Acta Automatica Sinica, 2025, 51(6): 1329−1346 doi: 10.16383/j.aas.c240566
http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c240566
关键词
物理信息机器学习,概念漂移,域适应,线性动力算子神经网络
摘要
基于机器学习的预测方法通常能够实现较高的拟合精度, 但模型可解释性和泛化性能较差. 在工业过程中, 由于概念漂移现象的存在, 这些方法的稳定性受到影响, 使得在复杂工业环境中精确建模成为一项既困难又具挑战性的任务. 为此, 提出一种基于线性动力算子的域适应物理信息神经网络方法. 首先通过历史工况数据建立线性动力算子神经网络模型, 捕获多变量时间序列数据的动态特性. 然后通过前向欧拉法对机理模型进行离散化, 构造物理信息正则化项, 促使模型服从机理约束. 最后通过最大均值差异对历史工况和当前工况下隐藏层状态变量进行分布对齐, 构建域适应损失, 降低变工况下数据分布变化对模型的影响. 在多个数据集上的实验表明, 该方法可以有效提高模型预测精度和泛化性能.
文章导读
随着流程工业生产过程复杂性的增加, 关键变量的精确测量因高成本和物理限制而受阻, 许多重要变量在实际操作中难以通过物理传感器直接测量[1]. 为此, 机理模型作为主要工具, 通过构建基于物理和化学规律的数学模型, 实现对关键变量的预测. 然而, 机理模型建模过程中进行较多的假设和一定的简化, 不可避免地影响模型的精度[2], 限制其在复杂环境中的应用. 随着数据获取和计算能力的提升, 数据驱动模型逐渐成为一种有效替代. 基于数据驱动的软测量方法直接利用过程数据来建立模型, 以预测关键变量, 在复杂工业系统中展现出巨大潜力[3−4]. 传统的多元统计方法, 如主成分回归[5] (Principal component regression, PCR)和偏最小二乘回归[6] (Partial least squares regression, PLSR)等机器学习方法, 尽管在某些特定应用中表现出色, 但非线性捕捉能力相对较差, 限制了其非线性建模精度. 近年来, 深度学习方法, 如卷积神经网络[7] (Convolutional neural network, CNN)、循环神经网络[8] (Recurrent neural network, RNN), 凭借其强大的多层次特征提取和非线性建模能力, 展示了在大规模数据环境下的巨大潜力. 然而, 传统的深度学习方法往往被视为一个黑盒代理模型, 其内部模型结构的复杂性和庞大的参数量导致对模型行为的有效解释变得极为困难[9], 并且存在泛化性差的问题.
基于深度学习的软测量方法通常依赖于大量的标记数据, 然而, 在诸多科学应用场景中, 这样的数据往往难以获取. 此外, 这类纯数据驱动建模的模型, 在预测结果方面往往缺乏与已知物理规律的科学一致性[10]. 因此, 模型所体现的参数关联特性与实际机理规律存在较大偏差, 在科研和工程实践中受到诸多限制[11−12]. 鉴于机理模型和数据驱动模型各自的局限性, 众多学者已着手探索机理与数据相结合的混合模型, 力求构建能精确反映系统物理特性的混合预测模型. 当前关于这种混合体系结构的术语使用尚未统一, 出现诸如“使用先验信息[13]”、“物理引导[14]”、“基于先验知识[15]”、“物理知情[16]”、“物理约束[17]”等多种表述方式. 物理信息神经网络[18−19] (Physics-informed neural network, PINN)近年来在机器学习领域取得显著进展, 并成为一个主要范例. PINN已被证明在模拟各种物理系统方面是有效的, 例如流体动力学[20−21]、工程力学[22−23]和流程工业[24] 等.
普通的PINN通常采用全连接(Fully connected, FC)层作为其基础架构, 然而, 网络中的参数数量庞大且相互作用复杂, 使得直接理解每个参数的具体功能变得十分困难. 这些神经网络参数对最终输出的影响高度抽象且间接, 缺乏直观的可解释性[25]. 为克服这一局限性, 最近的研究展示了算子学习在神经网络中的应用潜力, 例如深度神经算子网络[26] (Deep operator network, DeepONet)和傅里叶神经算子[27] (Fourier neural operator, FNO), 但这些方法通常需要大量的数据进行网络训练, 并且训练时间相对较长. 线性动力算子神经网络[28] (Linear dynamical operator neural network, dynoNet)提供一种不同的解决方案, 其核心要素是一个由有理传递函数描述的线性无限脉冲响应动态算子. dynoNet引入线性时不变(Linear time-invariant, LTI)动态层作为可微算子, LTI层具有良好定义的正向和反向行为, 可以使用传统神经网络的反向传播算法进行端到端训练. 在序列建模和系统识别方面, LTI层成功地近似了复杂的非线性因果动力学[29], 这种表示方法允许使用相对较少的参数来建模长期的时间依赖关系, 从而显著降低计算复杂度, 能够在保持模型复杂性的同时, 提高神经网络的计算效率.
在流程工业中, 由于生产设备老化或生产环境变化等原因, 使得不同工况的数据分布会随时间发生变化, 导致基于旧工况样本建立的模型不能适用于新的工况, 即存在概念漂移现象[30−31]. 近年来, 基于域不变表示的域适应[32] (Domain adaptation, DA)方法常用来解决因数据分布存在差异而导致模型预测性能下降的问题. Zhang等[33]提出一种域适应偏最小二乘算法, 利用目标域的少量标记样本来更新内模型的权值, 实现对潜在变量分布的自适应. Zhao等[34]通过域适应对齐不同分布数据的潜在变量二阶统计量, 解决概念漂移问题. 部分学者通过寻找历史工况和当前工况的域不变空间, 使用DA方法实现不同工况过程数据的分布对齐, 然后利用对齐后的数据建立回归模型实现最终的预测[35]. 其中, 关联对齐[36] (Correlation alignment, CORAL)通过线性变换方法对齐源域和目标域数据的二阶统计量, 提高无监督域适应预测效果. 迁移成分分析[37] (Transfer component analysis, TCA)通过增强源域与目标域中相似特征成分的一致性, 使不同域的数据分布在新的子空间内对齐. 最大均值差异[38] (Maximum mean discrepancy, MMD)是一种用于度量两个数据集之间差异的方法, 它能够量化不同工况下数据的分布差异. 通过计算不同工况下的数据分布之间的MMD值, 可以量化工况之间的差异程度. 基于这种差异, 可以调整优化模型或预测算法, 使其能够更好地适应不同工况下的数据分布. 为提高软测量模型对变工况的适应性, 研究域适应和物理信息融合的策略, 可以有效降低变工况下数据分布变化对模型的影响, 提高模型预测精度.
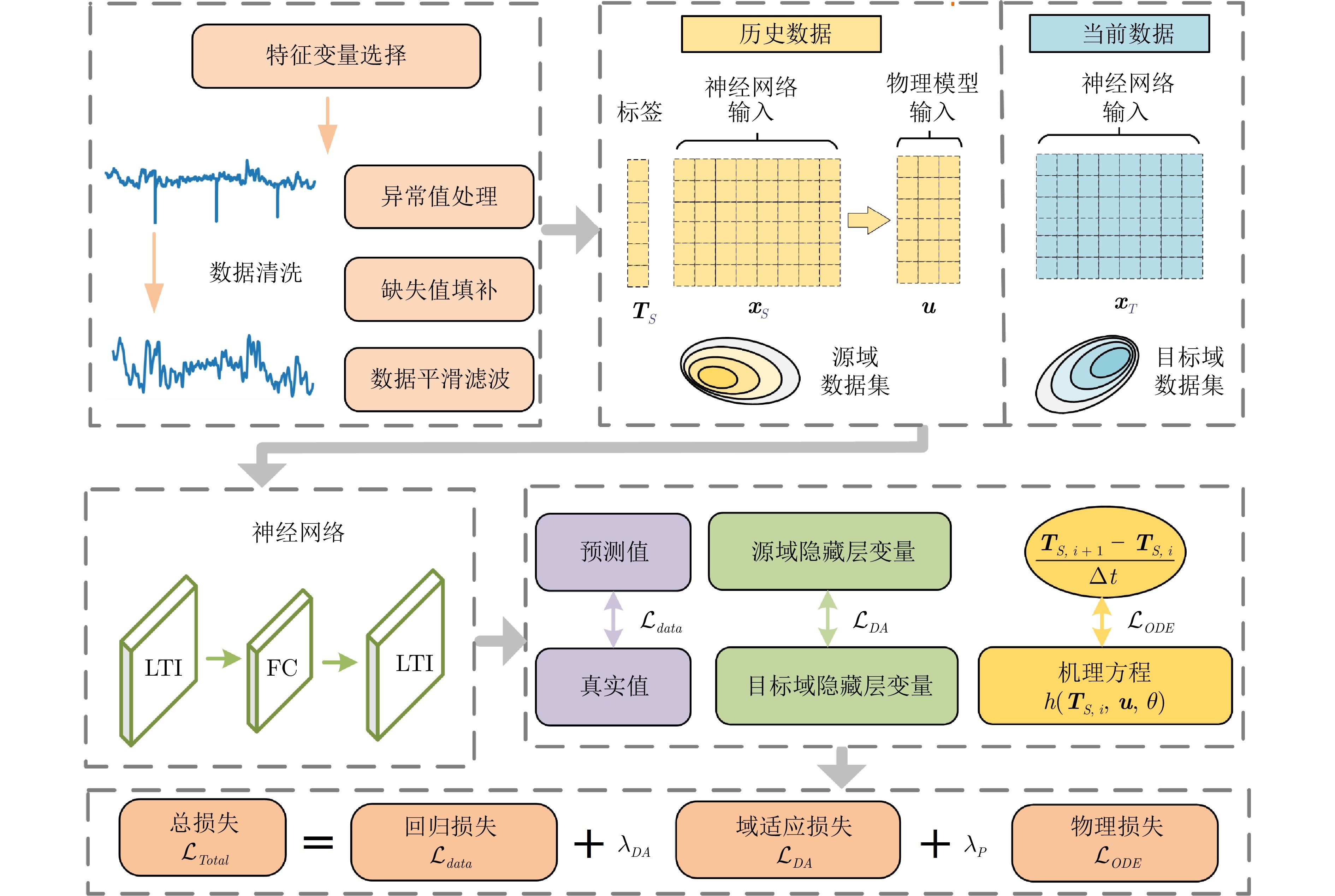
针对数据驱动建模存在的问题, 本文研究一种新颖的混合建模策略, 提出基于线性动力算子的域适应物理信息神经网络(Domain adaptation physics-informed neural network for linear dynamical operator, LDO-daPInet)方法. 图1展示数据预处理、数据划分和模型构建流程的整体框架. 首先, 对原始数据进行预处理, 以提高数据的可靠性. 将清洗后的数据划分为历史数据和当前数据, 用于模型的训练和预测. 划分后的数据被输入到LDO-daPInet模型中, 该模型由FC层和LTI层组成, 能够捕获多变量时间序列数据的动态特性. 然后, 机理模型利用前向欧拉法进行离散化, 生成包含物理信息的正则化项, 促使模型符合物理约束. 同时通过MMD方法对历史和当前数据的隐藏层状态变量进行分布对齐, 减少不同工况下数据分布差异对模型的影响. 最后, 通过最小化总损失函数来更新模型参数, 得到最终训练的模型. 本文的贡献如下: 1)提出一种域适应物理信息神经网络方法, 根据线性动力算子建立神经网络模型, 挖掘多变量时间序列数据的长时依赖性; 2)将机理模型通过前向欧拉法进行离散化, 构造物理信息正则化项, 对神经网络进行物理约束, 降低数据驱动模型对大量训练数据的依赖; 3)在物理信息神经网络中引入最大均值差异, 对历史工况和当前工况下隐藏层状态变量进行分布对齐, 构建域适应损失, 降低变工况下数据分布变化对模型的影响.
图 1 总体框架图
本文内容安排如下: 第1节回顾线性动力算子和物理信息神经网络的相关工作; 第2节给出本文所提方法的详细描述; 第3节对本文方法进行实验验证, 并对实验结果进行分析和讨论; 第4节进行总结与展望.
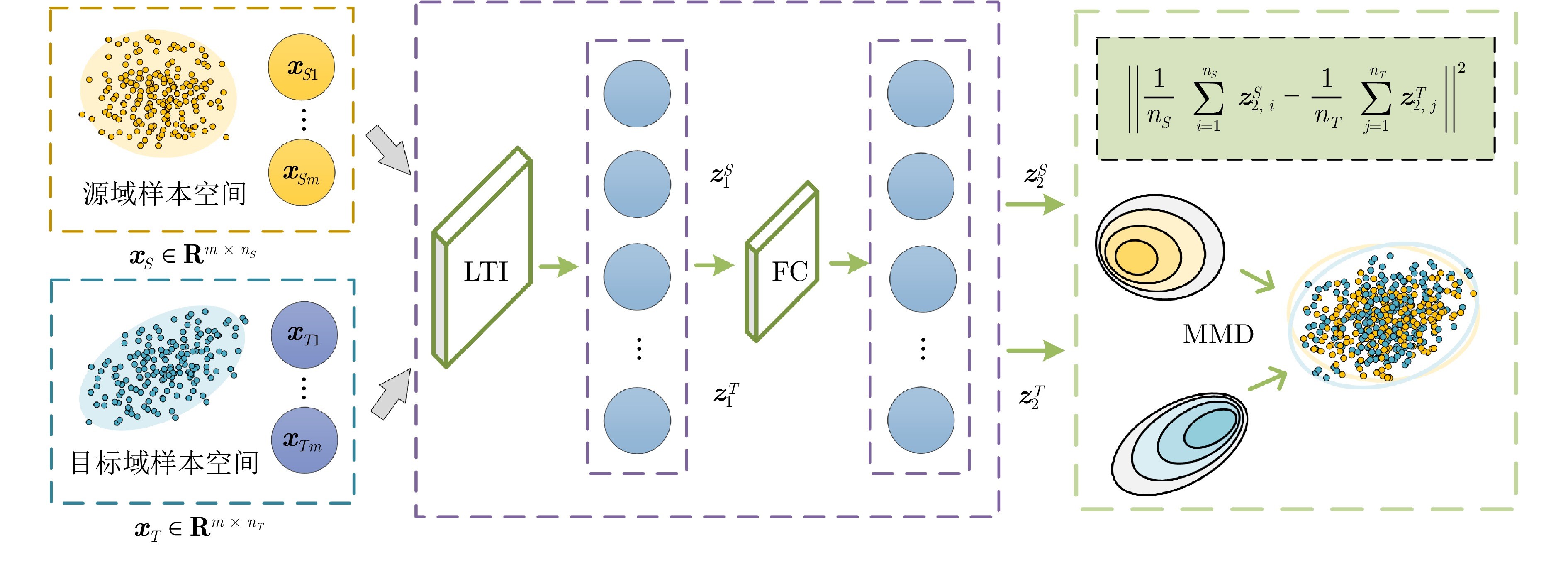
图 2 域适应框架图
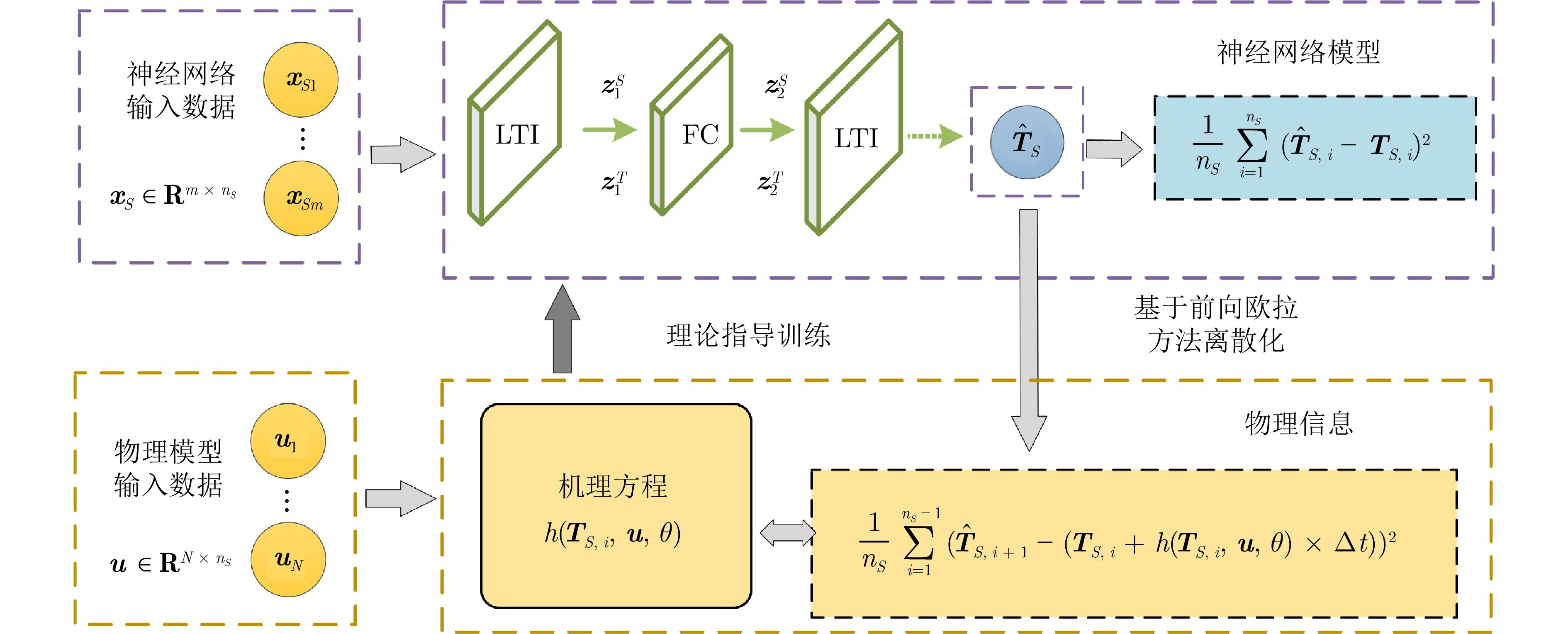
图 3 基于物理的约束机制
为了应对实际工业过程中由于工况变化等因素造成概念漂移下的预测模型失效问题, 提出一种基于线性动力算子的域适应物理信息神经网络建模方法. 利用有理传递函数来构建描述线性无限脉冲响应特性的动态算子, 进而构建能够反映系统动态特性的神经网络模型. 随后, 借助基于机理模型的物理信息融入, 促使模型服从机理约束; 同时, 应用最大均值差异的域适应方法, 降低不同工况下数据分布差异带来的影响. 通过仿真模型数据和实际燃煤发电过程数据对模型进行评估验证, 结果表明所提出的LDO-daPInet模型在变工况条件下能有效提高模型预测性能.
虽然本文实现了基于线性动力算子的物理信息神经网络建模方法, 并且通过域适应方法能够适应工况的变化, 但面对实际中的各种复杂情况, 还需要进一步深入开展理论和应用研究. 一方面研究自适应的权重优化方法和参数在线递推更新的变工况软测量方法, 另一方面探索干扰环境下鲁棒的物理信息神经网络建模方法, 以提高模型在复杂干扰环境下的实用性.
作者简介
曹力丰
太原理工大学电气与动力工程学院硕士研究生. 主要研究方向为软测量系统. E-mail: 18636531698@163.com
阎高伟
太原理工大学电气与动力工程学院教授. 主要研究方向为机器学习与人工智能, 软测量系统. 本文通信作者. E-mail: yangaowei@tyut.edu.cn
肖舒怡
太原理工大学电气与动力工程学院讲师. 主要研究方向为多智能体系统协同控制, 鲁棒自适应控制和容错控制. E-mail: xiaoshuyi@tyut.edu.cn
董珍柱
山西华光发电有限责任公司工程师. 主要研究方向为火电厂运行与控制. E-mail: hgfddzz@163.com
董平
山西华光发电有限责任公司工程师. 主要研究方向为火电机组热力系统动态建模及智能优化控制. E-mail: 15935164319@163.com
转载本文请联系原作者获取授权,同时请注明本文来自Ouariel科学网博客。
链接地址:https://wap.sciencenet.cn/blog-3291369-1495538.html?mobile=1
收藏