引用本文
陈鹏宇, 刘士荣, 段帅, 端军红, 刘扬. 基于梯度损失的离线强化学习算法. 自动化学报, 2025, 51(6): 1218−1232 doi: 10.16383/j.aas.c240481
Chen Peng-Yu, Liu Shi-Rong, Duan Shuai, Duan Jun-Hong, Liu Yang. Gradient loss for offline reinforcement learning. Acta Automatica Sinica, 2025, 51(6): 1218−1232 doi: 10.16383/j.aas.c240481
http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c240481
关键词
强化学习,离线强化学习,平坦最小值,梯度最小化
摘要
离线强化学习领域面临的核心挑战在于如何避免分布偏移并限制值函数的过估计问题. 尽管传统的TD3+BC算法通过引入行为克隆正则项, 有效地约束了习得策略, 使其更接近行为策略, 从而在一定程度上得到有竞争力的性能, 但其策略稳定性在训练过程中仍有待提高. 尤其在现实世界中, 策略验证可能涉及高昂的成本, 因此提高策略稳定性尤为关键. 该研究受到深度学习中“平坦最小值”概念的启发, 旨在探索目标策略损失函数在动作空间中的平坦区域, 以得到稳定策略. 为此, 提出一种梯度损失函数, 并基于此设计一种新的离线强化学习算法——梯度损失离线强化学习算法 (GLO). 在D4RL基准数据集上的实验结果表明, GLO算法在性能上超越了当前的主流算法. 此外, 还尝试将该研究的方法扩展到在线强化学习领域, 实验结果证明了该方法在在线强化学习环境下的普适性和有效性.
文章导读
近年来, 随着深度学习技术的飞速发展, 深度强化学习[1−2]在控制[3−4]、游戏[5−6]、电力调控[7−8]、医疗[9−10]、智能汽车[11−13]等多个领域取得显著的突破. 然而, 尽管深度强化学习展现出强大的能力, 但其往往依赖于与环境的频繁交互, 这在现实世界中可能带来高昂的成本和潜在的风险, 尤其是在自动驾驶、医疗决策、机器人控制等高风险领域. 为克服这些限制, 学者们提出离线强化学习[15−16] (Offline reinforcement learning, Offline RL)的概念.
离线强化学习的核心思想是利用历史数据集, 在不需要与环境实时交互的情况下, 通过分析和学习过去的交互数据来优化策略. 这种方法能够减少与环境交互的成本和风险, 但也带来新的挑战. 一个主要的问题是, 由于离线学习是在静态数据集上进行的, 这可能导致习得策略与数据采集时的行为策略之间出现分布偏移 (Distribution shift). 这种分布偏移会在策略评估和优化过程中引入外推误差(Extrapolation error), 即在面对数据集分布外的样本时, 离线强化学习算法所估计的值函数可能会产生较大的过估计, 导致策略性能不佳[15−16].
如何避免分布偏移, 限制值函数的过估计是离线强化学习所面临的核心问题之一. 一种有效的解决方法是限制习得策略与数据集行为策略之间的距离, 从而减少生成分布外动作的可能性. 这种类型的方法被归类为策略限制类方法. 例如, TD3+BC算法[17]在经典的TD3[18]算法框架上进行改进, 通过在目标函数中引入行为克隆[19] (Behavior cloning, BC)正则项, 并应用标准化技巧, 有效地限制了策略生成分布外动作. 这种方法通过较小的改进, 在学习效果和效率上展现出竞争力. 而SPOT[20]方法采用了变分自编码器(Variational autoencoder, VAE[21])来表示行为策略, 通过这种方式, 策略生成的动作被限制为接近VAE所编码的动作. 这种方法充分利用VAE的强大表示能力, 为策略学习提供一种新颖的约束机制. 此外, Diffusion-QL[22]算法则采用扩散模型[23]表示行为策略, 和使用正态分布表达策略相比, 扩散模型可以更好地拟合多峰分布的数据, 更准确地表达行为策略.
然而, 在实验中观察到, 在部分数据集下, TD3+BC算法的学习效果显现出一定的不稳定性[24]. 这种不稳定性限制了TD3+BC方法在更广泛场景下的应用潜力. 为克服这一挑战, 本研究从深度学习中的平坦最小值[25] (Flat minima)概念中受到启发, 并针对离线强化学习的特定背景进行创新性的改进, 提出梯度损失函数, 设计新的基于梯度损失函数的离线强化学习算法, 以增强策略学习的稳定性.
平坦最小值[25]的概念于1997年被Hochreiter和Schmidhuber提出, 这一理论在机器学习和深度学习领域具有深远的影响. 在深度学习中, 平坦最小值通常指的是在参数空间中具有较小梯度范数的局部最小值点. 在这些区域内网络的输出保持相对稳定不变. 这意味着, 即使参数在该区域内发生微小变化, 也不会导致损失函数的值出现显著的波动, 网络的性能不会受到显著影响. 因此平坦最小值通常被认为和模型泛化能力有密切的关系[25]. 一般而言, 当一个模型收敛到一个平坦的局部最小值时, 其鲁棒性会更好, 相反, 当模型收敛到一个尖锐的局部最小值时, 其鲁棒性较差.
在深度学习实践中, 寻找平坦最小值通常与损失函数对参数的梯度范数密切相关. 一种常见的策略是通过对梯度范数进行惩罚来引导优化过程向平坦最小值靠拢. 这种方法涉及对损失函数关于参数的梯度进行优化, 因此在优化过程中需要计算参数的Hessian矩阵. 然而, 在当前的硬件条件下, 直接计算和处理Hessian矩阵是极具挑战性的, 因为它不仅计算复杂度高, 而且存储需求巨大[26]. 为克服这一难题, 研究人员探究用替代方法来近似Hessian矩阵的特征, 例如利用一阶梯度的变体来间接地引导网络参数更新到参数空间中的平坦区域[26].
在离线强化学习领域也有类似的工作, Gao等[27]提出梯度惩罚方法, 该方法旨在减小Q函数关于其网络参数θ的梯度, 从而降低分布外动作对策略学习的负面影响. 通过在策略评估的损失函数中引入梯度惩罚项, Gao等鼓励Q函数保持一定的平滑性, 即Q函数对于输入动作的微小变化不应过于敏感. 并提出一种基于一阶近似的方案来计算梯度范数的梯度, 从而避免直接计算Hessian矩阵的复杂性. 这种方法在处理包含非专家策略的污染数据集时展现出较高的鲁棒性.
尽管Gao等的工作与本文在思路上有相似之处, 都通过引入梯度来改进离线强化学习算法, 但两者在目标和实现上都有本质区别. Gao等的研究聚焦于离线强化学习算法在非专家策略污染数据集上的性能下降问题, 关注值函数的准确性. 为此使用梯度范数正则项约束Q函数的平滑性来提升模型的鲁棒性. 然而, 现有离线强化学习算法在训练过程中仍面临不稳定问题. 为此, 本文提出梯度损失函数, 并设计基于该损失函数的离线强化学习算法, 通过寻找目标策略损失函数在动作空间中的平坦区域提高训练过程中策略的稳定性.
基于梯度的离线强化学习算法的目标是寻找目标策略损失函数在动作空间中的平坦区域, 并据此更新策略网络, 从而获得表现稳定的策略网络. 在D4RL数据集[28]上的实验结果表明, 梯度损失离线强化学习算法在多个任务中均表现出超越当前主流算法的性能, 证实了算法在解决TD3+BC算法学习不稳定问题方面的有效性, 显示了其在离线强化学习领域的应用潜力.
此外, 本研究还探讨将梯度损失函数作为正则项应用于在线强化学习环境的可能性. 实验结果表明, 即使在与环境实时交互的在线学习场景中, 梯度损失正则项同样能够提升算法性能. 这一观察进一步证实了梯度损失概念的普适性和强大潜力.
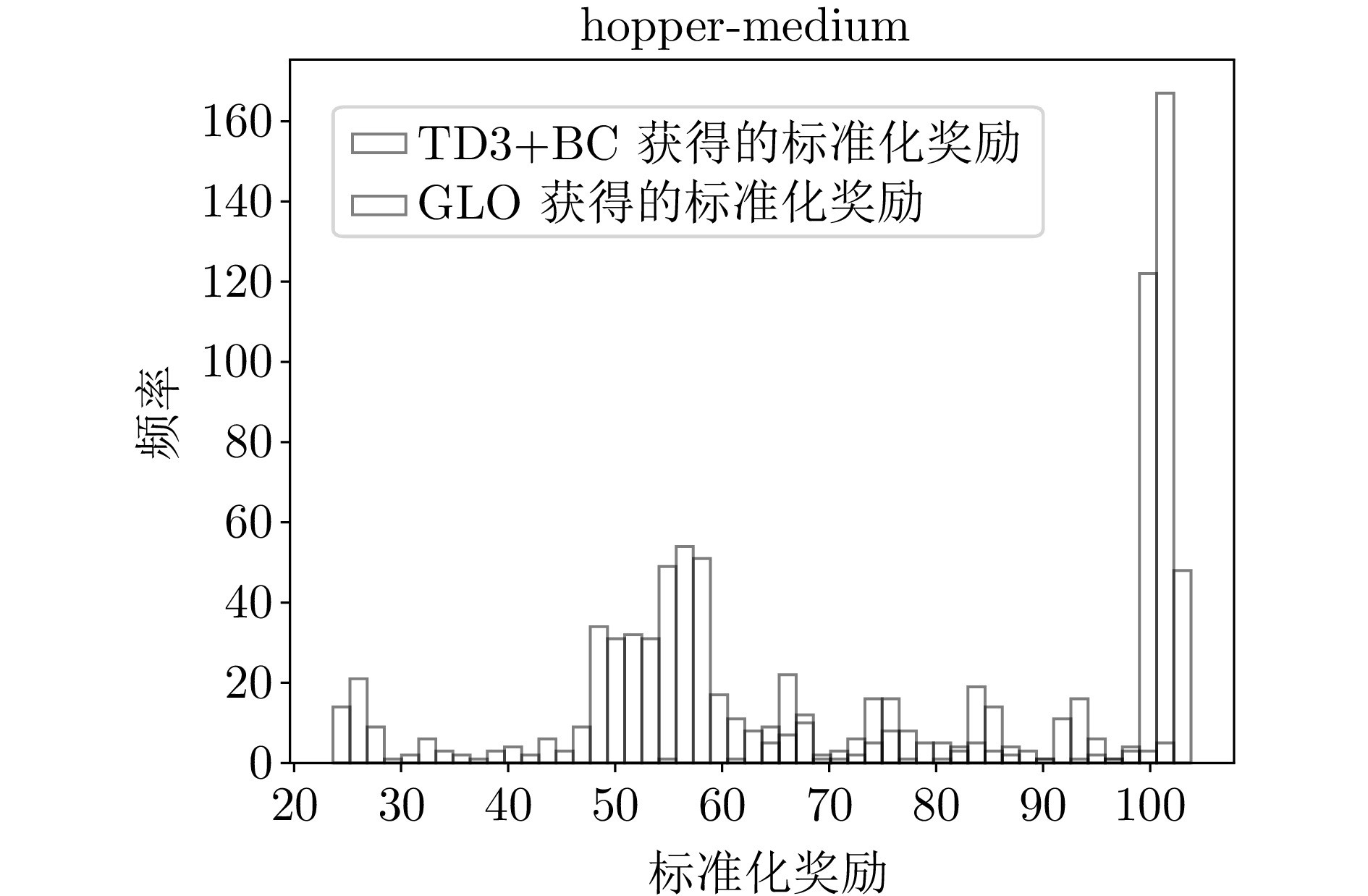
图 1 hopper-medium环境下的标准化奖励分布直方图
随着深度学习的发展, 深度强化学习在多个领域取得了显著的突破. 但受限于昂贵且危险的交互, 深度强化学习在实际应用中遇到了困难. 为了解决这一问题, 研究人员提出了离线强化学习, 但是由于只从历史数据集中学习的特点, 离线强化学习遇到了全新的挑战, 即避免学习中的分布偏移问题. TD3+BC是一种经典的离线强化学习算法, 通过策略约束来减小分布偏移. 然而, 该算法学习中的稳定性较弱, 为了解决这一问题, 本文结合深度学习中的平坦最小值概念, 提出了一种基于梯度损失的离线强化学习算法, 旨在解决传统离线强化学习算法训练稳定性较差的问题.
通过消融实验, 本文进一步验证了算法中关键结构的有效性. 并在超参数λ的作用分析中, 发现λ在不同质量的数据集下对算法性能有显著影响, 证明了λ在控制策略保守程度方面的作用.
本文提出的基于梯度损失的离线强化学习算法在D4RL数据集下的实验中展现出了优越的性能. 该研究成果为离线强化学习领域提供了新的视角和方法, 具有重要的理论和实践意义. 此外, 本研究还探索了梯度损失函数在在线强化学习中的应用, 实验结果表明, 在在线环境下, 梯度损失函数同样具有潜力.
转载本文请联系原作者获取授权,同时请注明本文来自Ouariel科学网博客。
链接地址:https://wap.sciencenet.cn/blog-3291369-1494110.html?mobile=1
收藏