引用本文

朱纪洪, 张骁骏, 杨赟杰, 袁夏明. 基于固定时间模型参考方法的倾转旋翼无人机姿态控制. 自动化学报, 2025, 51(5): 972−984 doi: 10.16383/j.aas.c240621

Zhu Ji-Hong, Zhang Xiao-Jun, Yang Yun-Jie, Yuan Xia-Ming. Attitude control of tilt-rotor unmanned aerial vehicle based on fixed-time model reference method. Acta Automatica Sinica, 2025, 51(5): 972−984 doi: 10.16383/j.aas.c240621

http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c240621

关键词

倾转旋翼无人机，姿态控制，固定时间收敛，模型参考控制，滑模控制 

摘要

倾转旋翼无人机动力学特性复杂, 过渡过程中的变速变构型特性导致系统具有较大的模型不确定性, 且容易受到阵风扰动等影响, 对姿态控制律设计提出很高要求. 针对该问题, 本文建立一种扰动观测器结合终端滑模补偿器的模型参考姿态控制方法. 基于齐次系统理论设计固定时间收敛扰动观测器, 实现对倾转旋翼无人机未建模动态和外部扰动的准确估计; 基于一种新型非线性饱和函数设计固定时间收敛终端滑模控制器, 结合低通滤波实现对指令的快速高品质跟踪; 为进一步解决控制奇异性问题, 提出在纵轴附近邻域对控制器的改进策略. 仿真结果表明, 所提方法在应对倾转旋翼无人机模型不确定性和外部扰动方面具有较强的鲁棒性, 相比基于有限时间稳定性理论的模型参考姿态控制方法, 固定时间收敛控制提供了更高的控制精度和更平滑的输出.

文章导读

常规构型的无人机(Unmanned aerial vehicle, UAV)可分为固定翼和旋翼两种类型. 固定翼无人机主要依靠机翼产生升力, 具有飞行速度快、效率高、航程长等优点. 然而, 其需要机场跑道或辅助设备起降且无法悬停, 限制了应用范围. 旋翼无人机通过旋翼产生的拉力直接抵抗重力, 具备优异的低速性能, 能够实现垂直起降和低空低速飞行, 但其前飞速度慢、效率低、航程短. 由此可见, 固定翼和旋翼无人机各有优缺点. 因此, 结合两者优势的新构型垂直起降固定翼无人机成为航空领域的研究热点, 其中一种重要构型是倾转旋翼无人机[1-2]. 

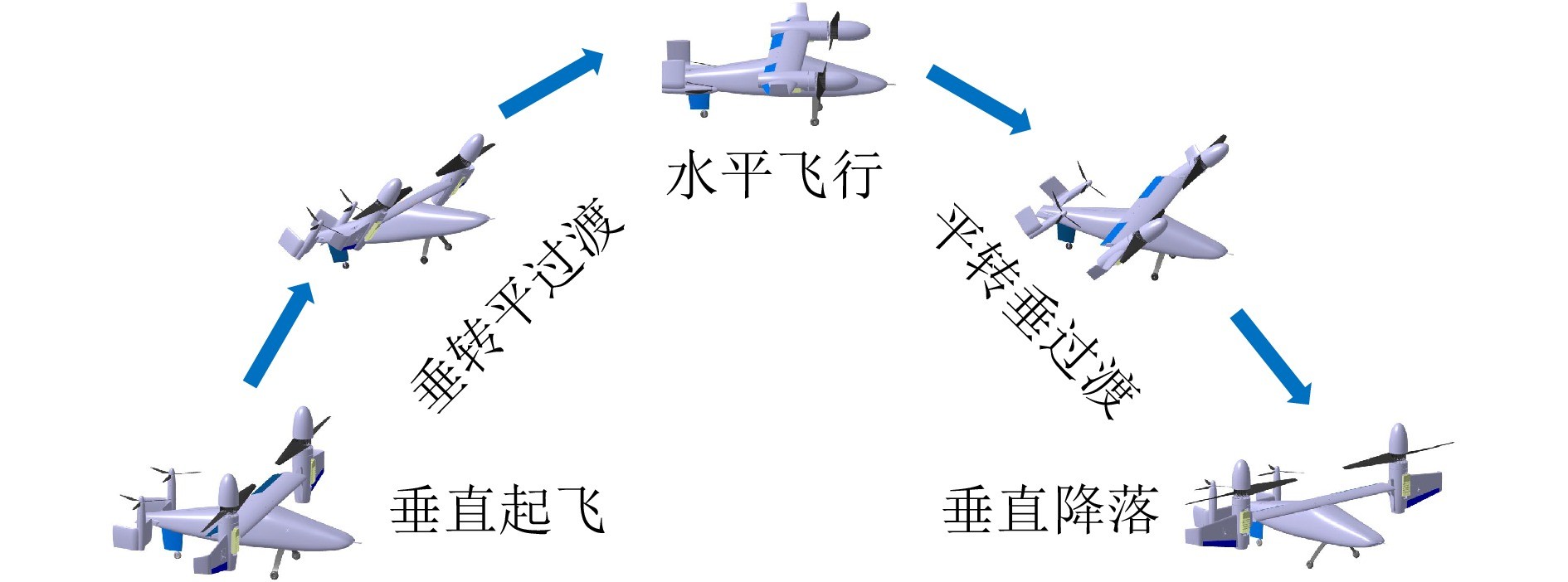
倾转旋翼无人机通过倾转旋翼/短舱合体来改变螺旋桨拉力方向, 实现垂直起降与高速平飞模式的转换. 图1展示倾转旋翼无人机的全包线飞行过程, 其典型飞行模式包括: 1)垂直起飞模式: 在该模式下旋翼/短舱处于90° 竖直状态, 螺旋桨拉力垂直于地面向上以平衡重力; 2)悬停转巡航模式(“垂转平”模式): 无人机达到一定飞行高度之后, 旋翼/短舱逐渐由垂直状态向水平状态倾转, 无人机逐渐加速至超过最小平飞速度; 3)巡航飞行模式: 即普通固定翼飞机飞行模式, 无人机可以达到较高的飞行速度和飞行效率; 4)巡航转悬停模式(“平转垂”模式): 在此阶段无人机减速, 旋翼/短舱逐渐由水平状态向垂直状态倾转以平衡重力, 最终达到悬停状态; 5)垂直降落模式: 无人机在悬停状态调整姿态和位置, 在预定地面降落. 可以看出, 在连接垂直起降与巡航飞行的“垂转平”及“平转垂”模式, 倾转旋翼无人机的短舱角和飞行速度都会经历大范围的变化, 在此过程中, 自由来流和螺旋桨滑流的耦合使得其动力学特性具有很强的非线性和未知不确定性, 尤其是气动特性的急剧改变、外界阵风的随机干扰等方面[3-5]. 同时, 推进系统带宽呈现出大范围时变特性, 不同阶段执行器对控制指令的响应快慢差异很大, 给姿态控制律设计带来挑战. 

图 1  倾转旋翼无人机全包线典型飞行状态

目前, 多种不同的线性控制律[6-9]和非线性控制律[10-13]设计方法在倾转旋翼无人机中得到了广泛的理论和应用研究. 其中, 模型参考控制是一种通过反馈被控对象与参考模型的输出或者状态误差, 使被控对象的输出跟随参考模型的控制方法[14-16], Anderson等[17]针对倾转旋翼无人机存在未知载荷和惯量不确定问题建立基于障碍李雅普诺夫函数的鲁棒模型参考自适应律, Liu等[18]针对倾转四旋翼飞机设计一种基于预测器的模型参考自适应横滚和偏航控制器, 用于补偿系统的不确定性和参数变化. 然而, 经典的稳定性理论难以确定系统收敛到平衡点的时间, 故而学者们在此基础上发展了有限时间稳定性理论[19-21]. 其给出与初始状态有关的系统收敛时间上界, 主要有李雅普诺夫理论[22]和齐次系统理论[23]两个发展方向. 固定时间稳定性理论是有限时间稳定性理论的进一步发展, 其收敛时间上界为固定值, 与初始状态无关[24-25]. 有限/固定时间稳定性理论可以应用于控制器和观测器设计, 由于快速性和鲁棒性, 其在飞行控制[26-27]、网络控制[28]、制导律设计[29]和多智能体控制[30]等方面得到广泛应用. 

相比于垂直起降和巡航飞行模式, 倾转旋翼无人机在“垂转平”和“平转垂”过渡过程中动力学特性变化快、模型不确定性强. 基于固定时间稳定性理论设计观测器可保证在固定的时间上界内得到对扰动的准确估计, 可应用于对强侧风等强时效性扰动的补偿, 提高闭环系统的鲁棒性. 本文基于固定时间稳定性理论, 将固定时间滑模控制器和观测器配合使用, 通过状态观测器实现闭环反馈, 通过扰动观测器实现不确定性补偿, 减小切换项增益和滑模控制器的抖振, 同时具有快速收敛特性, 提高倾转旋翼无人机过渡过程阶段飞行控制系统的鲁棒性. 

本文内容安排如下: 第1节给出倾转旋翼无人机姿态控制问题描述; 第2节对有限/固定时间稳定性理论的预备知识作简要介绍; 第3节介绍倾转旋翼无人机过渡过程阶段模型参考姿态控制架构; 第4节开展固定时间收敛扰动观测器设计, 证明观测器误差可在固定时间上界内收敛到零; 第5节开展固定时间收敛终端滑模控制器设计, 证明广义误差系统可在固定时间上界内收敛到原点; 第6节开展倾转旋翼无人机过渡过程姿态控制律仿真, 比较有限时间和固定时间收敛模型参考姿态控制方法; 最后, 第7节对本文进行总结与展望. 

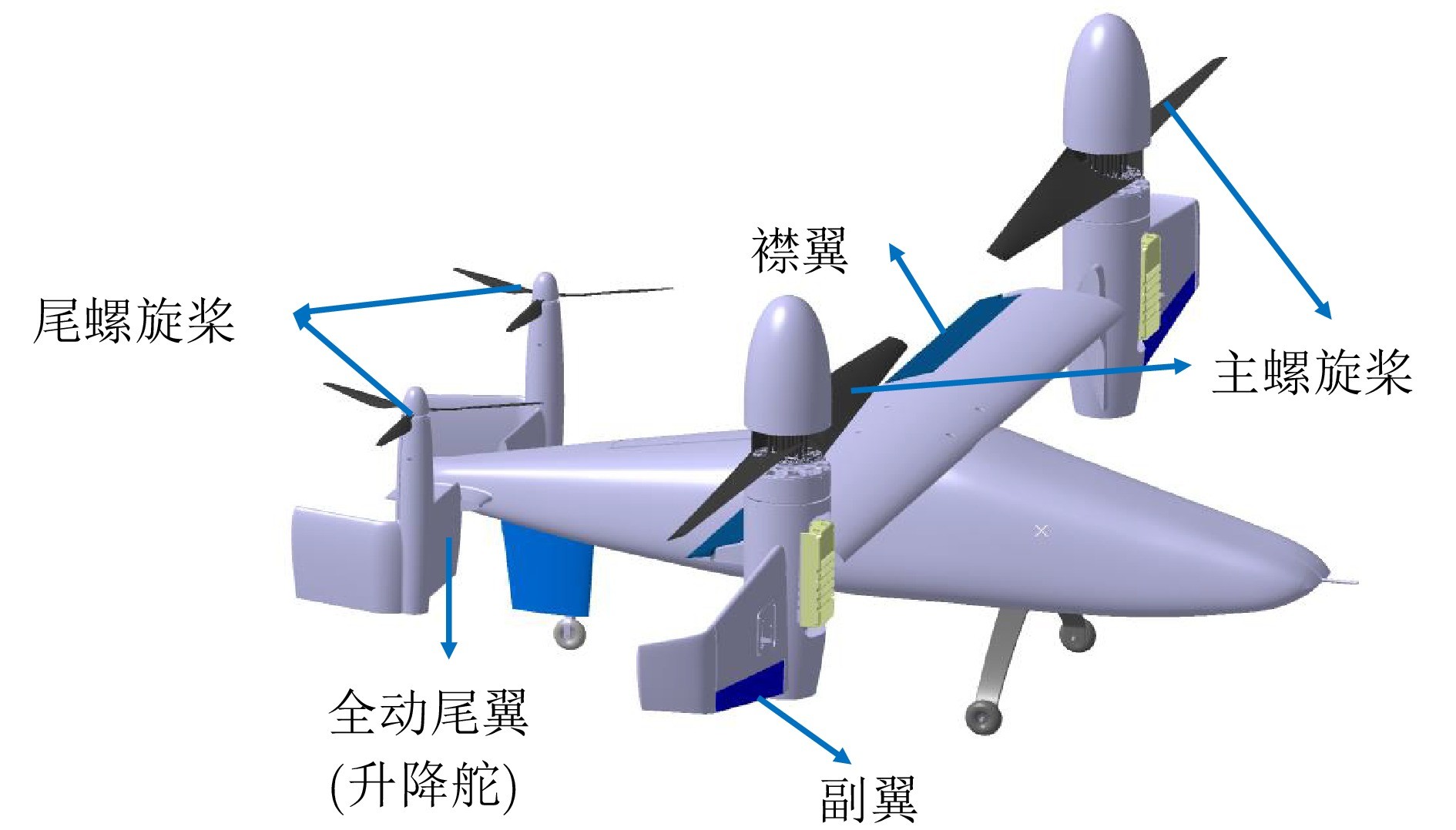
图 2  倾转旋翼无人机布局

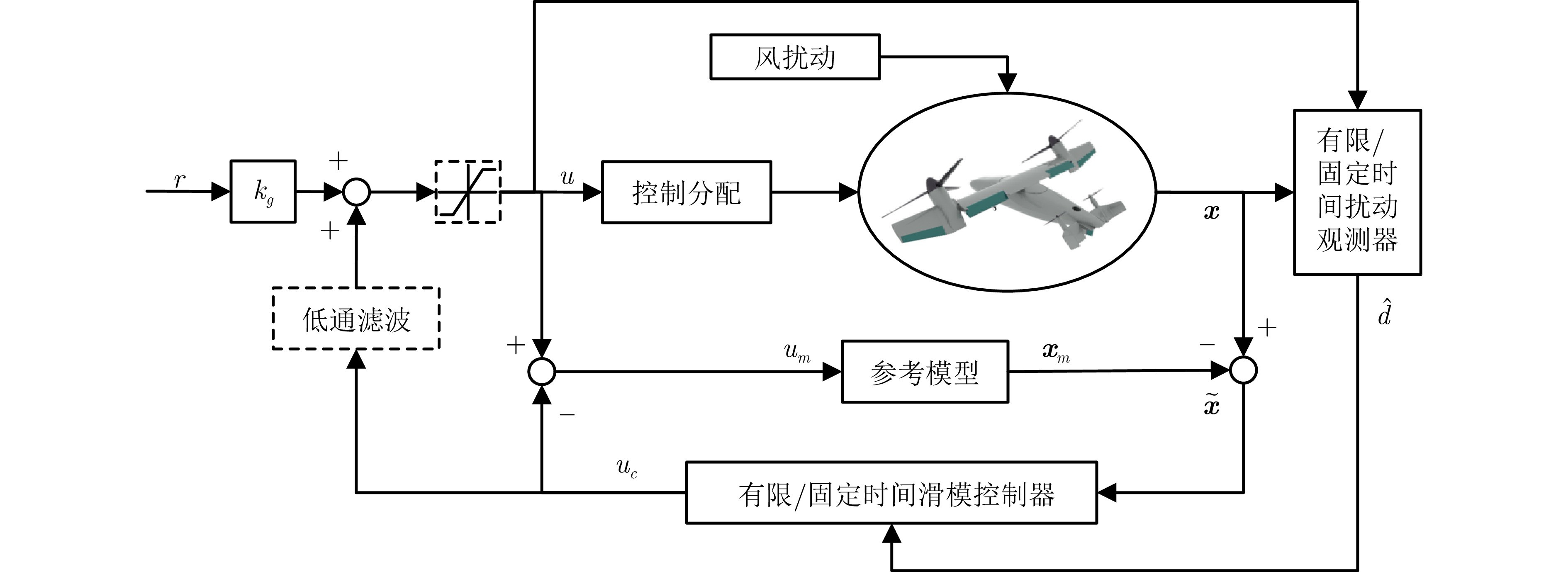
图 3  模型参考姿态控制器架构

针对倾转旋翼无人机飞行过程中模型不确定性大、易受外部扰动影响的问题, 研究基于固定时间稳定性理论的模型参考姿态控制方法. 通过滤波和限幅模块保证被控对象输入的平稳, 基于齐次系统理论设计固定时间扰动观测器, 基于非线性饱和函数提出固定时间终端滑模控制器设计方法. 仿真结果表明, 所提方法对模型不确定性和外部扰动具有较强的鲁棒性, 被控对象状态能够快速准确地跟踪参考模型, 保证了闭环动态特性和跟踪精度; 相对于有限时间方法, 固定时间模型参考控制方法具有更高的控制精度和更平滑的控制输出. 在未来研究工作中, 将对倾转旋翼无人机姿态控制中有限时间方法的系统收敛性和稳定性方面开展更深入的理论研究; 同时, 还将通过倾转旋翼无人机飞行试验, 对研究成果做系统性应用验证. 

作者简介

朱纪洪

清华大学精密仪器系、时空信息精密感知技术全国重点实验室教授. 主要研究方向为先进飞行器动力学与智能控制技术. E-mail: jhzhu@tsinghua.edu.cn

张骁骏

中航工业成都飞机设计研究所工程师. 主要研究方向为飞行器设计及飞行控制技术. E-mail: xj-zhang31@foxmail.com

杨赟杰

清华大学精密仪器系、时空信息精密感知技术全国重点实验室助理研究员. 主要研究方向为飞行动力学与非线性控制技术. 本文通信作者. E-mail: yangyunjie@tsinghua.edu.cn

袁夏明

清华大学精密仪器系、时空信息精密感知技术全国重点实验室助理研究员. 主要研究方向为无人系统及智能控制技术. E-mail: xmyuan@tsinghua.edu.cn