01研究背景
优化问题的求解一直是数学、计算机科学和工程领域的核心课题。在实际应用中,许多复杂系统的优化问题需要在有限时间内找到最优解,这对算法的收敛速度和计算效率提出了更高的要求。传统的优化方法如梯度下降法、牛顿法等,虽然在理论上能保证收敛,但在实际应用中由于计算资源有限、环境扰动、收敛速率慢等因素,往往难以满足高效求解的需求。
近年来,有限/固定时间(FxT)稳定性理论的发展为优化问题的求解提供了新的视角。FxT稳定性能够在一定的有限时间内(与初值无关)实现系统状态的稳定,这为设计加速收敛的优化算法提供了理论基础。此外,非光滑复合优化问题和包含方程约束的优化问题在许多实际应用中广泛存在,如机器学习中的正则化问题、网络控制中的一致性问题等,这些问题的求解对优化算法的鲁棒性和适应性提出了更高的要求。研究具有固定时间收敛的约束优化算法,这对需要实时响应和快速决策的应用场景具有重要意义,如自动驾驶和机器人控制等。研究干扰环境下具有鲁棒性的优化算法,可以提高系统的可靠性和适应性,确保在各种复杂环境中仍能有效运行。
02成果介绍
俄罗斯科学院院士、欧洲科学院院士、IEEE Fellow、东南大学曹进德教授及其合作团队提出了一种统一的固定时间梯度流(FxTGFs)算法框架用于求解约束优化问题。本文在目标函数满足Polyak-Łjasiewicz非凸假设下,针对无约束(含扰动)优化、等式约束优化和非光滑复合优化问题,基于固定时间稳定性理论,分别设计一阶(鲁棒)/二阶、投影以及近端FxTGFs,并提供了几种典型FxTGFs的静态遗憾分析。研究成果发表于IEEE/CAA Journal of Automatica Sinica 2024年第十一卷第八期:X. Shi, X. Xu, G. Wen, and J. Cao, “Fixed-time gradient flows for solving constrained optimization: A unified approach,” IEEE/CAA J. Autom. Sinica, vol. 11, no. 8, pp. 1849–1864, Aug. 2024. doi: 10.1109/JAS.2023.124089
加速方法在求解优化问题中的应用一直是一个引人入胜的话题。基于非线性动力系统的固定时间(FxT)稳定性,本文提出了一种设计FxT梯度流(FxTGFs)的统一方法。首先,本文提供了一类用于设计FxTGFs的通用非线性函数,在目标函数满足Polyak-Łjasiewicz非凸假设下,设计一阶FxTGFs;当梯度流中存在有界和消失的扰动时,进一步提出了一类具有抗扰能力的不连续鲁棒FxTGFs。在严格凸性假设下,给出了基于牛顿法的FxTGFs,并进一步扩展以解决时变优化问题。此外,本文还将所提出的FxTGFs用于求解含方程约束优化问题;针对非光滑复合优化问题,提出了具有广泛参数取值范围的FxT近端梯度流。
为了进一步展示各种FxTGFs的有效性,本文还详细提供了几种典型FxTGFs的静态遗憾分析,并得出结论:并非所有FxTGFs都有与初值无关的固定遗憾界限。最后,本文将提出的FxTGFs应用于解决两个网络问题,即网络一致性问题和线性方程组问题。通过选择分量保号的动力学函数,上述问题可以以分布式方式求解。
在实验仿真部分,本文设计了多个算例验证所提出算法的快速收敛性和鲁棒性。算例1为设计鲁棒的FxTGFs来求解干扰环境下逻辑回归问题,图1展示了算法在不同初值下的快速收敛性和鲁棒性能。
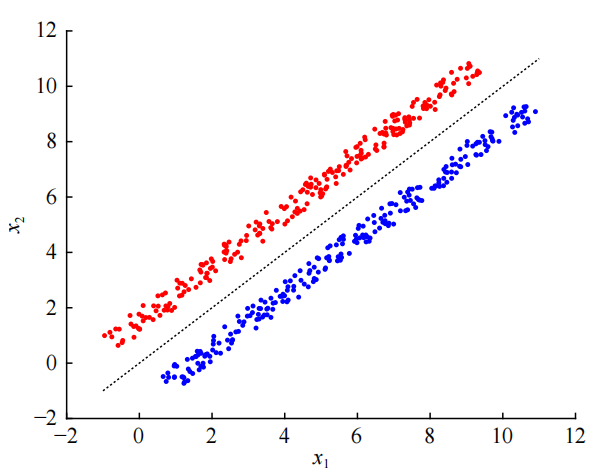
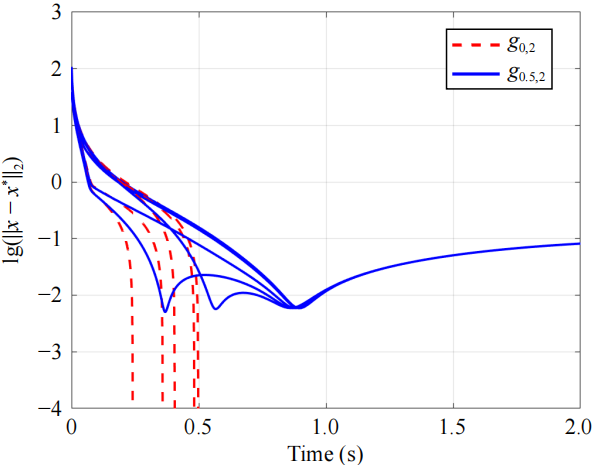
图1 算例1:鲁棒在带扰动的逻辑回归问题上性能(左图为数据点分布,右图为算法性能对比,其中g0,2则对应所设计鲁棒非光滑一阶FxTGF)
算例2为求解含有非光滑正则项、等式/集合约束的Lasso问题,通过将所提出FxTGFs与指数时间梯度流(EPGF)算法相比验证了所提算法的快速收敛性。算例3则为在扰动环境下求解线性方程组问题,仿真表明所提出非光滑分布式/集中式FxTGFs收敛时间均能实现固定时间收敛且表现出一定的鲁棒性能。
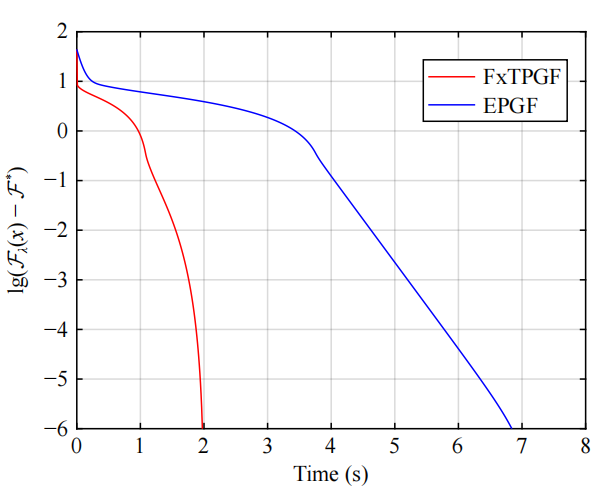
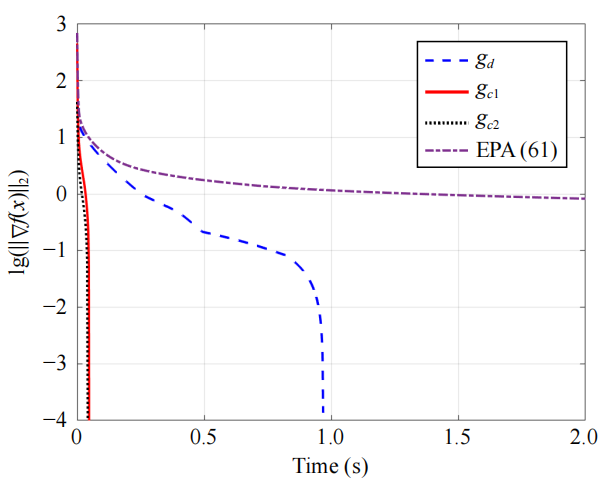
图2 算例2(左图):所提出FxTGFs与EPGF算法对比;算例3(右图):干扰环境下算法对比(gd对应所设计分布式算法,gc对应所设计集中式算法,EPA为现有算法)
总之,本文不仅在优化理论上提出了新型固定时间加速方法,还通过实际应用验证了这些方法在资源受限和扰动环境下求解复杂优化问题中的有效性和鲁棒性。
03作者及团队

时欣利,东南大学副教授,博士生导师,IEEE Senior Member,本、硕、博毕业于东南大学,曾获得江苏省优秀博士学位论文,入选江苏省双创博士、小米青年学者、江苏省科协青年科技人才托举工程,获ARC DECRA Fellow、东南大学授课竞赛二等奖和江苏省自动化学会青年科技奖(2024),主持国家自然科学基金面上/青年项目和科技部重点研发计划课题各1项,累计发表SCI权威期刊论文50余篇 (Automatica、IEEE/JAS汇刊30余篇),其中包含第一或通信作者论文30余篇。主要研究方向包括分布式学习与优化、多智能体强化学习等。

徐向平,东南大学助理研究员,入选东南大学至善博士后、江苏省“卓越博士后”,主持国自然青年基金、中国博士后基金特别资助和面上项目各1项,以第一或通信作者在IEEE TC/TITS/TSMCS/TASE等IEEE汇刊发表论文10篇。主要研究方向包括群体智能优化、路径规划和强化学习等。

温广辉,东南大学首席教授,博士生导师,2012年博士毕业于北京大学,第十八届中国青年科技奖、国家杰出青年科学基金获得者、国家优秀青年基金获得者、IET Fellow,获ARC DECRA Fellow,中国指挥与控制学会青年科学家奖,中国指挥与控制学会科学技术一等奖等学术奖励。持续入选科睿唯安高被引科学家榜单(2018-)、斯坦福大学发布的全球前2%顶尖科学家榜单(2019-)。主要研究方向包括自主智能系统,分布式控制和优化,强化学习等。

曹进德,东南大学首席教授、江苏国家应用数学(东南大学)中心主任、江苏省网络群体智能重点实验室主任。首届全国创新争先奖获得者,享受国务院政府特殊津贴。先后当选为俄罗斯科学院院士、欧洲科学院院士、俄罗斯工程院院士、欧洲科学与艺术院院士、立陶宛科学院院士、非洲科学院院士、巴基斯坦科学院院士、国际系统与控制科学院院士和IEEE Fellow等。长期从事复杂网络与复杂系统、神经动力学与优化和工程稳定性等研究,先后主持国家重点研发计划项目1项,国家自然科学基金项目9项(含重点项目),教育部博士点基金3项。
感谢本文作者提供以上简介
转载本文请联系原作者获取授权,同时请注明本文来自Ouariel科学网博客。
链接地址:https://wap.sciencenet.cn/blog-3291369-1489616.html?mobile=1
收藏

