崔雷

【摘要】在1976年Donald·Knuth提出Knuth’s Up-arrow Notation和2011年崔雷提出类似的广义幂指函数以来，本文讨论在定义 a^a=a^^2之后a^^0.5的问题。

1   幂指函数讨论基础

   历史上，在1976年Donald·Knuth提出Knuth’s Up-arrow Notation[1]和崔雷2011年独立提出广义幂指函数，其他有学者独立提出类似思想。

   在1976年，唐纳德（图灵奖获得者 ）在《Science》公开Knuth Up-arrow 的计数法，用他的写法是：

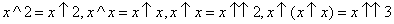
   三年后，Blakley在《Advance in Mathematics》严格定义了“ ”运算，并改动了写法：

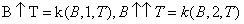
   这种运算的拓展由来已久，最早可以追溯至20世纪初超运算的递归函数理论研究。1928年，Wilhelm Ackermann提出Ackermann函数，首次系统化定义了运算层级的递推结构。此后，Goodstein（1947）将其形式化为超运算序列，涵盖加法、乘法、幂运算及更高层级。

   超运算序列 的递推定义如下：

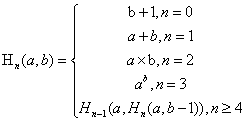
   除了上述表示外，通常还有以下记号法：

   标准符号记法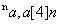 、高纳德箭号表示法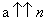、超运算符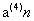、ASCII符号a^^n、阿克曼函数、迭代指数法、Hooshmand符号记法等。这些记为Tetration（后文称CF2函数）计数法。

   通常的分析历程是：

    a+a+a=a*3（3是加法中a的个数），a*a*a=a^3（3是乘法中a的个数），a^(a^a)=a^^3（3是幂指a的个数，此时称a^^3幂指函数的2阶3次，其中二阶指的是有2个“^”，3次指的是有3个“a”。2阶幂指幂指函数又称为迭代幂次）；

   此时可以继续推广至3阶等。一个不太严格的幂指函数（后称崔数函数）计算：

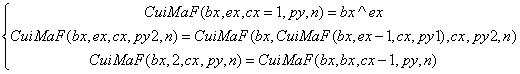
   这里面的bx是底数，就是前面举例的“a”；ex是指数，就是前面举例的3；cx为阶数，就是“^”的个数；px是前面的运算结果，n为顺序符。n顺序符指的是从原点向右的个数，这个对于多个值的表示是有用的。这里面的计算原则是：按照定义展开CuiMaF 函数，然后按照最里层先降次、降至2次后再降阶、然后依次向外展开，最终展开至幂函数。

   这种CuiMaF的推广并不是多余，因为对于前缀CuiMaF的崔数函数标记，对于bx、ex、cx、px存在一个假设：任意给出其中3个可得另一个。因此存在CuiMaFBP 之类函数，其中指的是Bx是自变量、Py是因变量。

   另外单独定义CMF2 、CF2函数如下：

CF2(bx)=CMF2(bx,2)=bx^bx=bx^^2 。实际上，对于a^^0.5 在目前的体系是无定义的（注意它不同于a^0.5 ）。那么可重新定义1 、 “/” 、 2符号，比如令：a^^2=b

    ，那么b^^(1/2)=a 。

   另外，对CMF2函数的指数另外定义“+ ”，即CMF2(bx,ex1+ex2) 和CMF2(bx,ex2+ex1) 并不相等（因为运算顺序的原因），这也是另行启用CMF2 函数的原因。

　　对于复合函数f(f(x))=g(x) 类型可以进一步形式化定义：CuiMaF(f(x),ex,0,g(x)) ，ex是复合的次数，这种复合函数定义为0阶崔数函数。

　　这种形式化定义用处是ex可以形式上定义为分数或者其他数。如果像崔数函数那样，重新定义 1 、“/” 、2之类的，就可以得到一个解释分支：

　　 CuiMaF(f(x),2,0,g(x))则 CuiMaF(g(x),1/2,0,f(x)) 。

   那么可把ex=1/2 称为半迭代、把ex=1/3 称为1/3 迭代。此时，CuiMaF的0阶1/2 次类似于朗伯W函数（Lambert's W Function）。

2   分数次拓展的核心问题和Kneser解析延拓

　　上述重新定义“/”是解决分数次拓展的一种办法（也是其中一个解释分支），而更常见的办法是Kneser的解析延拓方法。而此时分数次拓展主要是解决：

　　连续性扩展：如何将离散的运算层级映射为连续函数；

　　唯一性保障：是否存在唯一合理的扩展方式；

　　实际应用：分数次运算能否描述物理的渐进过程。

　　在1950年Kenser解析延拓提出来后，通过复分析工具构造全局函数，成为分数次CF2 函数的常规处理方法，然后应用 Schroder 方程与线性化解决计算问题。

　　Knser函数计算2^^0.5 的结果通过：

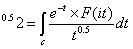
　　其中C为特定积分路径，此时按照Kneser的方法给出2^^0.5≈1.459。

2.1 一般的认为Kneser解析延拓F(z)满足条件

　　1.连续性：分数次结果在整数点与经典定义一致。整数点锚定F(n)=a^^n  和递推关系F(z+1)=a^F(z) 。

　　2.光滑性：运算在非整数处可导且解析。

　　3.唯一性：在特定约束下存在唯一合理的扩展。

　　此时Kneser复分析工具应用以满足：

　　1. 周期性消除：通过选择特定参数化消除指数函数的周期性干扰。

　　2. 积分变换：利用积分公式将离散迭代映射为连续解析表达式。

　　3. 唯一性定理：通过强制函数在复平面上的解析性和渐近行为，确保解的唯一性。

2.2  Kneser的核心技术

　　1. Schroder方程：通过求解函数迭代的不动点方程 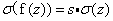（其中s为乘子），将迭代问题转化为线性问题。

　　2. 复平面上的积分表示：通过积分变换（如傅里叶变换）将离散迭代步骤映射为连续的解析表达式。

　　3. 周期归一化：强制函数在虚数方向上的周期性衰减，消除多解性。

2.3  不动点的泰勒展开

假设函数f(z) 在不动点z0处满足f(z0)=z0 ，将f(z)在z0附近展开为泰勒级数[2]：

f(z)=z0+s(z-z0)+a/2*(z-z0)^2+...

其中：s=f(z0) 为一阶导数（乘子）；高阶项如二次项(z-z0)^2 反映非线性效应。一阶项主导的条件：当  |s|≠0且|s|≠1  时，一阶项 s(z-z0)主导局部行为。

2.4  不动点函数f(z)线性化的条件和局限性

　　1. 双曲不动点（|s|≠1 )：泰勒一阶项主导，可局部线性化。

　　2. 中性不动点（ |s|=1)：需引入共形映射或花瓣理论。

　　3. 非解析点：泰勒展开失效，Schroder方程不可用。

3 分数次CF2函数的Kneser解析的挑战

   Kneser 方法的关键步骤依赖于通过 Schroder 方程将CF2函数运算线性化，进而延拓到复平面。若 Schroder 方程失效：

   全局解析延拓受阻：无法通过线性化工具构造光滑函数 F(z)，导致分数次迭代的定义失去数学基础。

   唯一性丧失：周期性或多值性可能导致无穷多潜在解，无法满足 Kneser 方法中解析函数的唯一性要求。

   实际上，CF2 函数 x^x导数为x^x*(1+ln(x)) 。z^z 的对数项导致分支点奇异性将导致函数Schroder 方程将迭代幂运算线性化失效，另外Schroder方程在泰勒展开中导函数比原函数更复杂其二次项不能省略且不属于2.4节所述情况。

   这样，函数无法通过 Schroder 方程（即略去二次项的泰勒展开）展开为线性函数，且无法复平面积分表示，从而失去了其Kneser解析延拓的合理性。

   而验证前述2^^0.5约等于1.459 的计算，可以通过2^^1.5继续迭代0.5次（同时解释了CMF2 函数的引入意义），此时先计算2^^1.5迭代0.5次和2^^0.5继续迭代1.5次并不能得到 。

4   结论与展望

   4.1 Kneser方法通过复分析工具扩展了幂指函数至分数次层级，但其有效性依赖函数的解析性和双曲不动点。在函数的计算中，Schroder方程在比原函数更复杂的导函数场景中失效，需引入更复杂的数学工具。

   4.2 在研究复平面积分表示时，在当初代数基本定理公开时，人们尚未意识到函数的存在，进而复平面也有待于拓展。函数揭示了传统解析延拓方法的局限性。

   4.3 分数次的崔数函数是可以有多种解释的，进一步的，分数阶是研究方向。

   4.4 其他的 CMF2函数，比如 CMF2(bx,m)其中m为3以上整数时，能否表示其他典型超越数，也值得进一步推广。

参考文献

[1]Knuth, D.: Mathematics and Computer Science: Coping with Finiteness [J].Science, 1976, 194(4271):1235-1242.

[2]钟玉泉.复变函数论（第2版）[M].北京:高等教育出版社,1988