40. 能否制造出完美的光学透镜?
Can researchers make a perfect optical lens?
从目前的情况来看,这个问题似乎已经被基本解决,所以这个问题目前的状态好像是Close,有下图为证。

图1 关于光学完美透镜的相关新闻报道
所谓的完美透镜就是理论上能够以最完美的清晰度还原物体而成像的透镜,也就是物体上的任何光点所发出的所有光经过透镜后都能完美聚焦为一个相同光点的透镜。然而实际情况是:从物体上某个光点发出的光波经过有限尺寸的透镜系统后都会发生不可避免的衍射;另外物体上光点所发出的光可能因具有不同的频率,经过透镜后会产生色差(可以理解为不同频率的波经过透镜后的焦距不同),这些因素都会使像点变大;而且物体上所发出的光波由于不可能被有限透镜系统完全搜集,有些光波会不可避免地损失;而进入透镜的光波也会因为透镜的不平整或材料的不均匀,造成光波相位的偏差而使像点发生形变;即便透镜平整、均匀和纯净,物体光点的不同分波在经过透镜后也会不同程度地被透镜吸收甚至被完全消耗掉,比如振幅很小的分波被透镜吸收而消失,而表达细节的很弱的倏逝波 (evanescent wave)也因为振幅很快衰减而消失,这样经过透镜后的光点不仅会变大、变形和变暗,而且光点内的强弱细节信息也因为倏逝波衰减而彻底失去。

图2 艾里光斑和瑞利判据
所以实际透镜的分辨率,在不考虑透镜材料、工艺、吸收等其他因素下,可以统一用光学成像的衍射极限来表达,即远场光学成像的分辨率本身就存在一个极限,也就是透镜成像能分辨不同光点间的最小尺度有一个下限,约为成像光波波长λ的一半。当然更为严格的光学成像分辨率极限被称为瑞利判据(Rayleigh criterion),两个光点经过光学透镜后会衍射成光斑(称为艾里光斑),因光斑重叠而不能分辨的最小距离为:d = 0.61λ/NA,其中NA = n sinθ为透镜环境系统的数值孔径(NA:numerical aperture),和物镜介质折射率n和透镜的孔径θ有关(如图2所示)。这个分辨率使得物体光点的尺寸在下降到瑞利极限d以下时,成像的光斑就不会再变小,如图3所示。

图3 成像物体尺寸和成像光斑尺寸
而完美透镜是指可以突破瑞利极限实现亚波长尺度成像的透镜,也就是像点没有色差(消色差)、没有形变,也没有任何光波损失的成像透镜。实际上1928年Synge就提出超越瑞利衍射极限进行成像的建议,1968年Veselago提出了负折射率材料能对光线进行汇聚成像的设想。然而直到32年后的2000年,Pendry再一次提出了利用平面负折射材料可以制造“完美透镜”的概念和理论。而2014年获诺贝尔化学奖的超分辨荧光显微技术也仅仅是利用其他辅助方式来突破瑞利极限而成像的技术(关于超精细成像方面可参考Nature论文),其虽然和完美透镜的目标相同但研究的内容是不尽相同的。
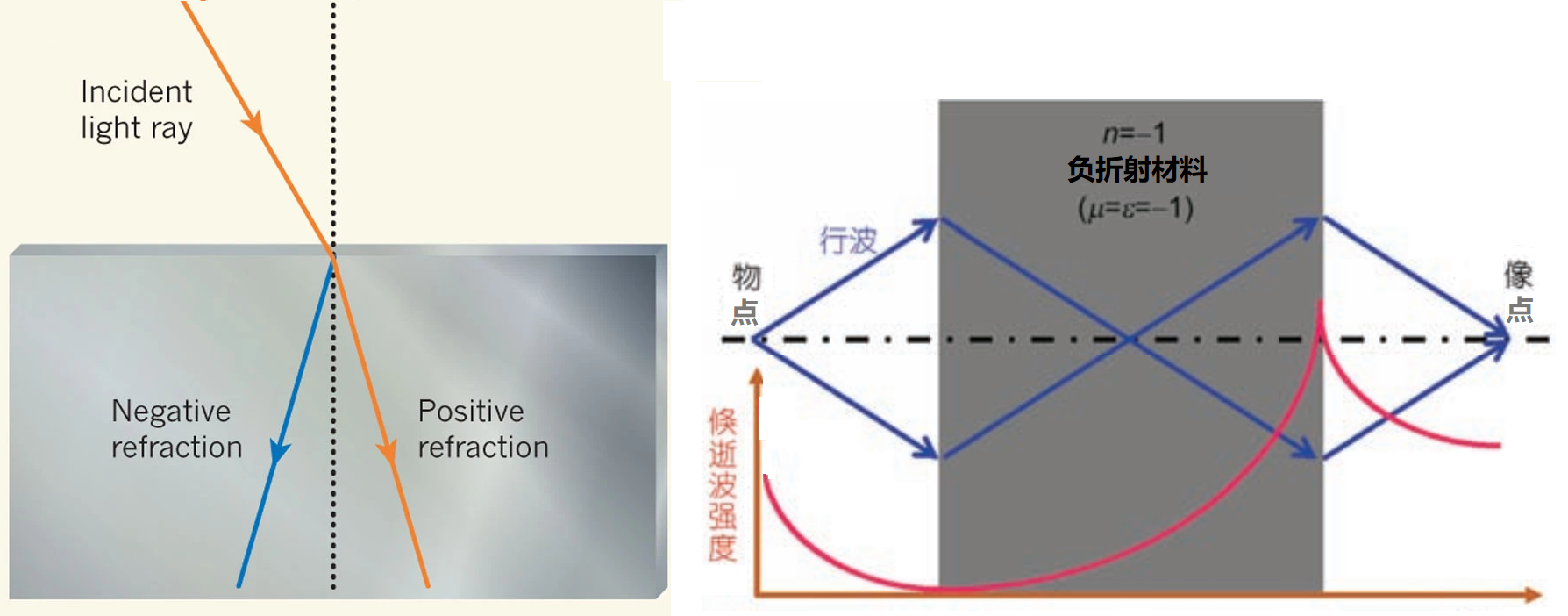
图4 负折射材料及完美透镜理论
Pendry在其提出完美透镜的著名论文“负折射实现完美透镜(Negative Refraction Makes a Perfect Lens)”中认为,一直被成像所忽视的携带物体结构细节的倏逝波可以在负折射材料中被放大从而实现更高分辨率的成像(当然理论存在很大争议,有人认为对倏逝波的放大会让电磁场的能量变得很大而导致不自洽,但实验上却证实负折射材料确实可以放大倏逝波实现亚波长的完美成像)。在Pendry工作的启发下,2001年人们利用超构材料(metamaterial)实现了微波段的负折射,开启了超构材料的新时代。

之后2004年人们利用具有负折射率的超构材料很快就在微波段实现了Pendy所提出的完美透镜。然而由于超构材料微结构加工技术的瓶颈,能对更短波长产生有效相干调制而损耗很小的超构材料一时难以实现,虽然近年来利用微结构中更细微的表面等离子体共振激元可以产生非常理想的负折射偏转,但表面等离子激元的损耗一直是一个无法克服的障碍,所以可见光段的完美透镜一直都没有突破。这也就导致了本问题的出现:能不能制造出可见光波段的完美透镜?而在本文开头的那个2013年的新闻只是美国标准技术局Lezec教授研究组实现了紫外波段负折射材料的报道(见图5可参考他们的Nature论文),而不是真正实现了光波段完美透镜的技术方案,所以沿着这个问题前进的道路仍然不会有尽头。
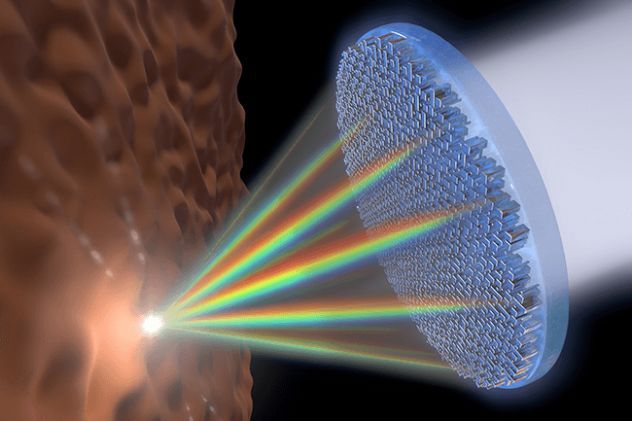
图5 超构材料构成的超透镜
转载本文请联系原作者获取授权,同时请注明本文来自张林科学网博客。
链接地址:https://wap.sciencenet.cn/blog-318012-1389223.html?mobile=1
收藏

