内容提要:湍流的各向异性是由湍流的产生机制所决定的。湍流的产生是流向速度发生速度间断(奇点),产生了流向速度的脉动,由此通过质量连续性和动量方程依次导致了另外两个方向的速度脉动,这样的过程,决定了湍流必然是各向异性的。
(一)湍流的各向异性(anisotropy)的认识进展
定义:如果湍流流场里的湍流物理量及其统计规律与空间位置无关,就称为湍流为均匀的(homogeneous),否则就称为是非均匀的(inhomogeneous)。如果湍流流场里的湍流物理量及其统计规律与空间的各个方位方向无关,就称为湍流为各向同性的(isotropy),否则就称为是各向异性的(anisotropy)。
在上个世纪30年代,人们发现湍流是一种杂乱无章的不规则运动,进而认为湍流可能是随机运动。随之,Taylor和冯卡门在一些假定条件下,于1935年和1937年相继提出了湍流的均匀各向同性理论。
1941年,前苏联数学家Kolmogorov基于英国气象学家Richardson的旋涡级串假设,利用统计力学方法和无因次分析,提出了均匀各向同性湍流的标度律(K41理论)。此标度律有三个假设,(1) 高雷诺数湍流的局部小尺度运动是均匀各向同性的准稳态流动;(2) 高雷诺数湍流的局部小尺度湍流的统计特性只取决于耗散率和粘度;(3) 高雷诺数湍流的惯性子区局部小尺度运动只取决于耗散率,而和粘度无关,即惯性子区耗散率是一个常数 【1-2】。
根据上述三个假设,Kolmogorov得出的惯性子区的湍流能谱标度律的-5/3幂次律,与高雷诺数下的大多数实验数据接近,也有很多数据相差较大。
直到1950-1960年代,人们发现了湍流中存在大尺度运动,但是仍然认为这些大尺度运动是不规则的运动。
1967年,美国斯坦福大学的Kline等人,经过对湍流边界层的氢气泡实验,发现了壁面湍流的拟序结构,而且发现这种结构是由于湍流猝发而产生的。1974年美国加州理工学院的Brown and Roshko在混合层实验中发现了湍流的准周期的拟序结构。从此之后,人们认为湍流中确实存在大尺度的有规则的拟序结构,但是对于小尺度的湍流运动,还是不清楚,认为小尺度的运动可能仍是随机运动 【1-2】。
那么,在一些文献中,就有了这样的提法,湍流的大尺度运动是有规则的拟序结构,小尺度运动是随机运动。因为是随机的,这样小尺度运动就是各向同性的。后来的实验统计规律显示,湍流的小尺度运动,也不是各向同性的【3-4】。可是湍流各向异性的产生机理一直不清楚。
人们发现,壁面流动里的湍流,都是各向异性的,就把引起各向异性的原因归于是壁面引起的。但是,实验也显示了,尾迹流动和射流流动以及网栅流动里的湍流,也都是各向异性的。这样,自由剪切流动的湍流也是各向异性的,就不能把引起湍流各向异性的原因归于是壁面引起的。 把各向异性的原因归于是壁面引起的,这样的明显的错误的文章,都发表在了流体力学的顶级期刊上,误导了读者。
最近的研究表明,湍流的各向异性,在惯性子区的旋涡级串的小尺度里一直存在,一直持续到湍流的耗散区的Kolmogorov尺度上【3-4】。
也就是说,自然界和实验室里的湍流都是各向异性的,无论尺度多么小,根本不存在什么各向同性的湍流。那么,湍流各向异性的原因到底是怎么产生的呢?
(二)湍流的各向异性(anisotropy)的根源
过去,人们一般通过湍流的统计特性,分析湍流量的非正态分布及雷诺应力张量或应变率张量的特性,分析湍流的各向异性,但是对各向异性的本质不知道。作者认为,湍流的各向异性的根源,应该从湍流产生的原理上去解释,不能仅从现象上去理解。140多年来,因为湍流产生的原因不知道,所以各向异性的原因就找不到。
现在,湍流产生的原因已经弄清楚了,湍流是奇点导致的,这样,湍流各向异性的根源就找到了【5-8】。根据能量梯度理论,湍流的各向异性不是壁面引起的,是湍流产生的机制决定的。
根据窦华书的能量梯度理论,在湍流产生过程中,速度的三个分量的脉动,u', v', w', 不是随机均等出现的。在临界条件下,由于奇点的爆发,此位置流向速度理论上突变为零,这样u'先发生了(一般u'=-(30%~70%)u),流体突然减速,这样流体微团就受到压缩。根据质量连续性方程, 垂直于流动方向就会膨胀,导致v', w'出现(图1所示),所以三个速度脉动分量它们不是均等出现的【5-7】。因为u'是主动的,是"驱动力",v', w'是被动的,因此就产生了各向异性【8】。
因为,u'先发生,同时它从主流u带来了来流速度的能量,然后才传给了 v', w',这解释了湍流是怎么从平均流动获得能量的【5-7】,这就是Kolmogorov的K41理论的能谱标度律的左边的能量输入区的大涡能量的来源。详细过程是这样的,对于由奇点产生的大涡,u'为负的,根据连续性方程,v'和w'都是正的,它们的峰值几乎是同步的,这已经得到了计算结果的验证(如图2)。而它们的具体大小是通过流体微团的应变率张量变化决定的,即由连续性方程和动量方程联立求解决定的。
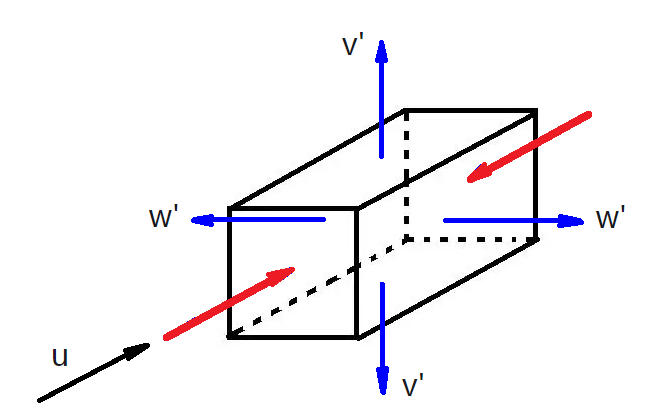
图1 奇点位置的流体微团,流动方向的速度u由来流的u突变为零,流体微团突然受到流向压缩(红色箭头所示),那么,在横截面上就会膨胀或拉伸,导致了y和z方向脉动速度的产生。注意,对一个质点,y和z方向脉动速度都只能产生一个方向的速度,图里画了可能的2个方向。
现在,用一个形象的例子来帮助大家理解一下。圆管内的流动,是无数根流束在流动,可以看作是一捆煮熟的面条。当有扰动时,每一根面条都在波动运动前行。波峰处面条拉伸,波谷处面条压缩(不是眼睛看上去的波峰和波谷,而是速度随时间变化的波峰和波谷),即波峰处速度最大,波谷处速度最慢 (图3所示)。当达到一个临界值,波谷达到临界,成为了瞬时奇点,速度发生间断,出现了负的spike,这就是-u' (可以理解为因压缩而蹦掉)。因为流体微团符合质量连续守恒定律,在y和z方向就会产生拉伸,这就有了v',w'。在最初的临界点,奇点爆发时,u'是负的,v'和w'都是正的(如图1)。这样,-u'和+v'形成了猝发,产生了最大的湍流剪切应力-u'v'(第二象限的burst 或者叫上抛 ejection,通俗说,就是被挤爆了),而+w'形成了旋涡的展向拉伸。
再举一个例子,高速公路上行驶的汽车,以速度u1前行,有一辆车突然停止,理论上速度变为u=0,由于惯性和地面摩擦力相互作用,实际上此刻速度可能是变为比如u=0.3u1,速度变化就是-0.7u1)。然后,后面的车辆追尾,就是这样的突然压缩,前面那辆车上的货物被挤压向四周蹦散,这就有了v'和w'(如图1)。
上面的关于湍流产生的描述,理论与DNS/LES计算和实验完全一致,无论是壁面剪切流动,还是自由剪切流动【1, 9, 10】。对于圆球绕流,来流是轴对称的,尾迹里产生的湍流也是和壁面流动一样,通过奇点产生上抛,以及引起下掠【9,10】。因为湍流是u'导致的,而且它提供了能量,所以在任何湍流中,u', v', w',这三个速度脉动分量,u'的幅值永远是最大的,如图2。图中蓝色的是流向速度的脉动,是最初产生的spikes(奇点)。每一个奇点产生一个旋涡。也就是湍流中每一个旋涡的中心都是奇点。对于更小一级的奇点,产生原理是相同的。所以,对于逐级产生的旋涡,都不可能各向同性。

图2 圆球绕流尾迹中的奇点位置的瞬时速度随时间变化(奇点产生的临界条件下)。纵坐标为各个速度分量;横坐标为时间。均为无因次变量【9】。在临界条件下流向速度所产生的奇点(蓝色的spikes的最低处的尖点)。蓝色的流向速度的负的spike与黑色的v形成了上抛运动,即猝发burst。
图2中是圆球绕流尾迹中,随着雷诺数的增大,在最初奇点产生的临界条件下的三个速度分量随时间的变化。可以看出,在这个临界条件下,在这个尾迹的中分面上(z=0),湍流漩涡几乎是二维的,相对于u'和v',w'非常小。平板边界层流动的转捩过程发卡涡的中分面上也是这样的。为什么会这样呢?因为这是在临界雷诺数,奇点爆发时,u'和v'形成了上抛(ejection),当然在垂直于上抛的方向上,速度就非常小。随着雷诺数增大,三维性越来越强,奇点位置w'的值越来越大,完全发展的湍流中,w'达到u'和v'的同样数量级。
100多年来,人们认为壁面剪切流动里的湍流(如边界层流动;圆管流动;槽道流动;平面Couette流动;Taylor-Couette流动)与自由剪切流动里的湍流(如尾迹流动里面的卡门涡街;射流;混合层),产生机理是不一样的。研究发现,这两类湍流的产生机理完全一样,都是NS方程的奇点导致的湍流,产生机理一样,湍流结构一样【9,10,5】。
(三)湍流不存在随机运动
上面讲到,根据湍流产生的原理,速度的三个分量的脉动,u', v', w', 不是随机均等出现的。u'是起到支配作用的。对于有机械功输入的流动,如旋转流动,叶轮机械内部的流动,由于流线方向的支配作用更显著,各向异性特性更强。因此,湍流运动都不是随机的。湍流不是随机的原因就在这里,是由湍流的产生机制所决定的。
湍流是确定性的方程,确定性的边界条件,导致的确定性的流动。湍流里面充满了旋涡,每一个漩涡的中心都是奇点。每一个奇点的出现都是由Navier-Stokes (NS)方程所决定的。
湍流产生及能量传递的具体过程是,流向速度u 通过奇点(速度间断)把能量传递给了u',u'通过质量连续性和动量方程,把能量传递给了v'和w',以及p’。
1930~1970年那些年,人们把湍流看做是随机运动,那是受当时的对湍流的认识水平所限。那些年走的弯路,不是没有作用,让后人知道了那些方法和路径是走不通的,这就促进了湍流研究进展。
湍流大尺度运动是确定性的,小尺度运动也是确定性的。为什么这么讲,因为作者已经精确地证明了,对于湍流,NS方程存在唯一解,只是由于奇点存在引起了解的不光滑【8】。众所周知,对于层流,给定NS方程和初值及边值条件,NS方程就有确定的唯一解。而对于湍流,就是在层流流场里,增加了一些奇点,实际上就是增加了更多的Dirichlet边界条件,这样NS方程仍有唯一解,只是奇点附近的解是不光滑的。可以这样说,湍流是NS方程的奇异解。需要指出的是,由于奇点产生多出来的Dirichlet边界条件是动态的,且奇点是一闪而过,奇点在空间的位置也是变化的(湍流中的流线不是光滑的),因此,在数值计算中,随着雷诺数增大,只有足够小的时间步长和网格尺寸才能比较准确地计算出来。
根据我们几十年的计算流体力学的经验,已经明白了,湍流是存在唯一解的。如果没有唯一解,大家就不能那么顺利地计算出结果了。正因为存在这个唯一解,不同作者的计算结果都趋于向这个唯一解逼近,不同作者的计算结果才可以互相比较。雷诺数越高,需要网格越密,就是因为NS奇异性以及解不光滑。
从另一方面看,如果湍流是随机运动,那么,Navier-Stokes方程的DNS计算,还好使吗?如果湍流是随机运动,那么驱动随机运动的“动力”是什么?作为经典力学所描述的宏观的流体质点运动,湍流中不存在驱动随机运动的力的来源。
(四)小结
湍流的所有物理现象,都必须根据湍流产生的机制来解释,才能是可靠的。特别是,对于湍流中的任何物理现象的解释,必须依据瞬时的速度分布来进行。看不到瞬时速度分布变化,而做出的解释,那只能叫猜测。本文依据能量梯度理论的湍流产生原理,依据理论的和计算预测的瞬时速度分布,成功地解释了湍流的各向异性现象。
能量梯度理论解释了湍流的几乎所有现象,例如,预测了湍流是怎样通过扰动引起湍流产生的,解释了湍流产生的奇点、湍流的猝发、间歇性、拟序结构、各向异性、能量来源,漩涡正级联,逆级联【10】,湍流的维持机理,雷诺数趋于无穷大时的反常耗散 (anomalous dissipation), 等等。理论与DNS/LES计算及实验结果获得了完美的一致。
参考文献
1. Tennekes, H., Lumley, J. L., A first course in turbulence,MIT Press, 1972. 2. Pope, S. B., Turbulent Flows, Combridge University Press, 2000. 3. Blair, M. F., Boundary-Layer transition in accelerating flows with intense freestream turbulence: Part 2—The zone of intermittent turbulence, J. Fluids Eng., 1992, 114(3): 322-332. 4. Chowdhuri, S., Banerjee, T., Quantifying small-scale anisotropy in turbulent flows, Phys. Rev. Fluids, 9, 2024, 074604. 5. Dou, H.-S., Origin of Turbulence-Energy Gradient Theory, 2022, Springer. https://link.springer.com/book/10.1007/978-981-19-0087-7 (全书下载地址). 6. Dou, H.-S., Singularity of Navier-Stokes equations leading to turbulence, Adv. Appl. Math. Mech., 13(3), 2021, 527-553 . https://doi.org/10.4208/aamm.OA-2020-0063 (AAMM); https://arxiv.org/abs/1805.12053v10 (Arxiv) (通过物理学推导出奇点) 7. Dou, H.-S., No existence and smoothness of solution of the Navier-Stokes equation, Entropy, 2022, 24, 339. https://doi.org/10.3390/e24030339 (通过数学推导出奇点) 8. Dou, H.-S., Structure of solutions of the Navier-Stokes equation at existence of singularity, Preprint, submitted to a Journal, October 2024. (证明了NS方程的解是唯一的,但不是光滑的。即湍流是NS方程的奇异解) 9. Niu, L., Dou, H.-S.*, Zhou, C., Xu, W., Turbulence generation in the transitional wake flow behind a sphere, Physics of Fluids, 36, 2024, 034127. https://doi.org/10.1063/5.0199349
10. Zhou, C., Dou, H.-S.*, Niu, L., Xu, W., Inverse energy cascade in turbulent Taylor–Couette flows, Physics of Fluids 37, 2025, 014110. https://doi.org/10.1063/5.0250908
转载本文请联系原作者获取授权,同时请注明本文来自窦华书科学网博客。
链接地址:https://wap.sciencenet.cn/blog-3057857-1479188.html?mobile=1
收藏

