圆周率的一个计算方法
鲍海飞 2023-4-24
数学最神奇的地方,是它的普适性,只要有兴趣,找到自己关注的兴趣点,无论是简单的问题,还是复杂的问题,谁都可以拿出纸来画图、计算和证明。
而数学上,最神奇的一个数字便是π(Pi)。圆周率pi是一个无穷不循环小数,具有随机性和无规律性。1947年,美国数学家伊万-尼文(Ivan Niven)用微积分和反正法证明了它是无理数。Pi的计算方法大致有几类,割圆法、分析法、沙-波法,椭圆积分法、概率法等。割圆法是作圆的内接或外切正多边形来计算多边形的周长或面积。分析法包括连分数法、级数法、以及利用反正切函数法等。
Pi的计算涉及两个简单的小问题,一个是计算的精度,一个是计算的效率。计算的精度是指接近真值的程度3.14159……,而计算的效率是说采用什么方法和步骤能达到最快计算出该数值。自然,计算的精度和效率将与方法和复杂度有关。
看到微信上有人演示pi的计算方法,不由心动,亦突发奇想,自己也想算一下这个数学上最神奇、最古老的数字。几何法具有非常好的直观性,也采用所谓的割圆法,但却是不对称的割圆法。或许有人尝试过这种方法,但不管别人是否利用过该法,我还是按照我的思路简单计算一下。
计算方法简单如下所描述。即选择一个正方形,假定其边长为1,在其中一个对角线上截取内部一个圆弧,即为四分之一圆,亦即圆的半径为1,如图1所示。取正方形的上边长和左侧边长的二分之一处,连接该两点,计算图中三个线段的长度和(姑且看作一个简单的弧线,红线所示),就是计算图1中a-b-a的长度。长度b的数值通过简单的勾股定理就可以计算出来。得到结果如下:
2a+b=
。
图1
在图1的基础上,在其每个线段的中点处继续截取,连线,得到如图2所示的计算图示,既需要计算图中2(a+b)长度(红色曲线)。同样利用勾股定理可以计算b和d的长度。
得到结果如下:
如果大家对数字感兴趣的话,那么一定会发现,上面这个数如果减掉1之后就是黄金分割数。
图2
在图2的基础上,依次继续在其每个临边的中点处连线,得到如图3所示的计算图示,即需要计算图中2(a+b)+c的长度。此处可见,线段连线越来越接近圆弧。同样利用勾股定理分别计算出b和c的长度。得到最终5个线段的长度和,结果如下:
如果对此数不敏感的话,那么简单做个运算,就可以得到:1.57075X2=3.14150。这个数大家不陌生,这就是Pi。上述计算√10(根号下10)取值是3.162,√2(根号2)取小数为1.414。
如果把√10和√2取的位数多一些,上述计算就得到1.5708995,再乘以2之后便得到3.1417990。同pi(3.1415926535)值比较一下,取小数点后3位,计算得到精度就很高了。理论上,四分之一圆弧的长度为Pi/2,即为3.14159/2=1.570795…。
至此,经过三个步骤就得到了这一结果。实际上相当于在一个完整的圆上截取了16个线段。这个方法,具有高中、甚至初中数学知识就可以计算出来。
图3
为何能够得到较高的计算精度?显然,上述的作图略显夸张,四分之一圆弧和正方形的位置和比例不是很恰当。上述计算得到的精度,可以从直观的尺规作图得到确认和解释。图4是利用尺规所做的一个圆和其四分之一的正方形。从图中可以看出,真正的边长截取,第一次为二分之一处,第二次取四分之一处,到第三次的八分之一处就难以再截取下去了,因此,图3中的第三次操作后的线段a-b-c-b-a就已经非常接近圆了。
应该指出的是,上述的计算应该可以找到递推的计算通式,另外,可以预见,所截取的线段,有的跨越在圆外,有的可能在圆内,导致该方法的结果。(这可以进一步通过计算圆心到正方形对角线和所截取曲线的距离作计算来估计。实际上,正方形对角线的距离为√2(根号2),也即圆心到正方形对角线顶点的距离。而正方形的顶点到第一次正方形边长二分之一处截取的线段其距离为√2/4 ,而圆的半径为1。(√2-√2/4-1)=0.086〉0。显然,这是计算Pi精度高的原因)
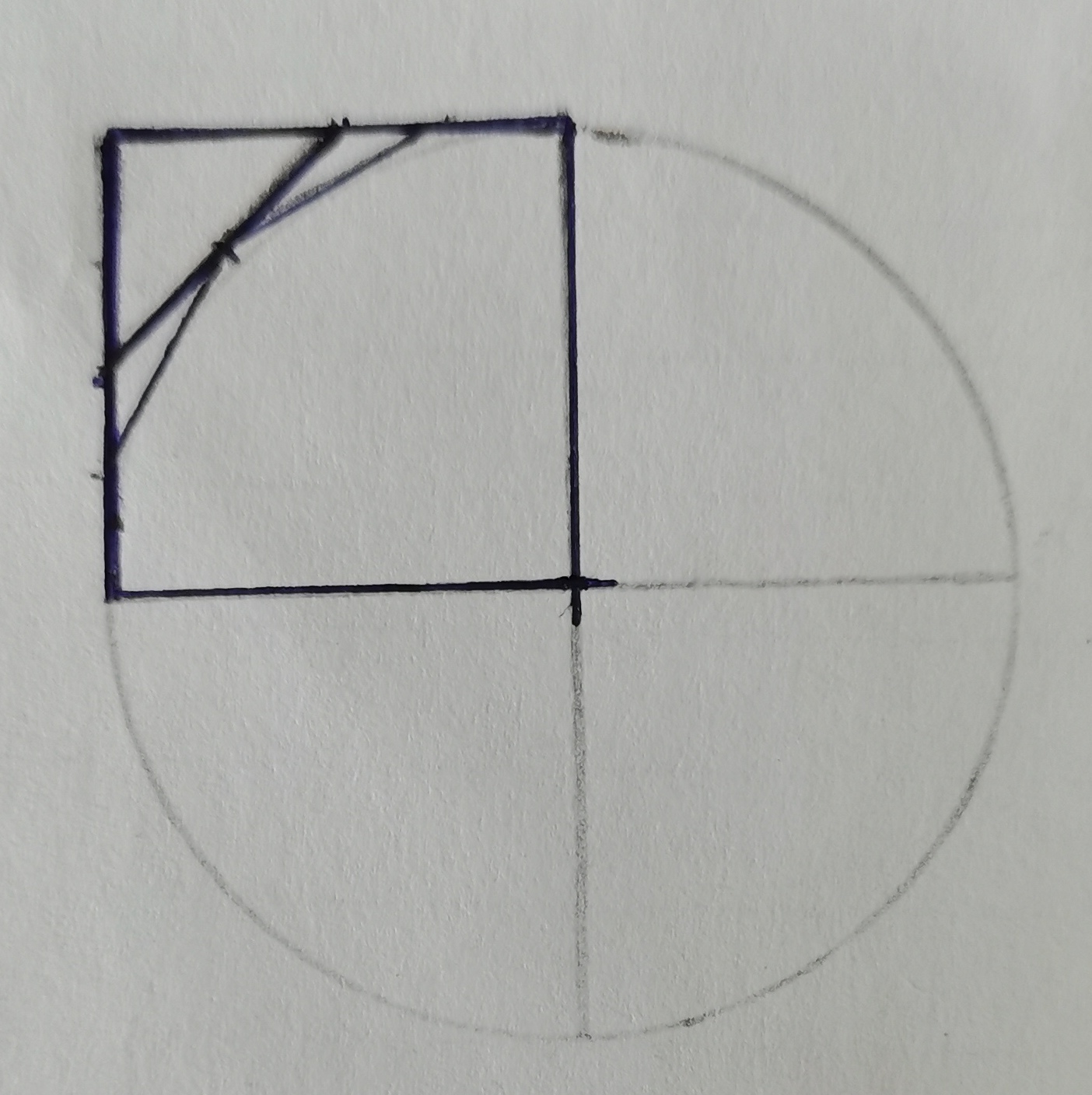 图4
图4
从古至今,许多人对pi痴迷。
中国的刘徽(225-295)计算了3072边形,得到了圆周率上界3.1416,下界为3.1415。
截止到2021年8月,pi已经计算到小数点后62.8万亿位。这需要具有不小于316TB内存的超级计算机才能做到,用于超算性能的检测。据说,航天局工程师能用到圆周率后15位。如果某一天,科学家若能利用到后40位,那么人类就可能精确计算出可观测宇宙的大小误差。
如果有一天,pi被某台计算机算尽了,得到的不是无穷不循环小数,那么会有什么影响呢?这个问题也一直困扰着我。但我终于找到了答案:如果圆周率被算尽,是有理数,那就意味着,世界并不存在真正的圆。所谓的圆滑曲线,都是由无数个小线段组成,这就会使得几何学中的图形发生变化,所涉及的计算思想和方法也都会存在错误。其后果是,微积分的理论和方法将会被颠覆,数学大厦也将不复存在,所有的科学测量标准,也需要全部重新考量。
人类创造了数,人类发现了数字中的奥秘,而正是它的无穷无尽才引导着我们一直向前探索,寻找着宇宙的无穷大和无穷小。
转载本文请联系原作者获取授权,同时请注明本文来自鲍海飞科学网博客。
链接地址:https://wap.sciencenet.cn/blog-278905-1385580.html?mobile=1
收藏

