多项式求根是科学计算中最基础、也最核心的问题之一。许多看似无关的应用——从控制系统的稳定性分析、量子化学的本征值计算,到 5G 信号处理中的滤波器设计——最终都归结为求解一个多项式方程:
$$f(z)=z^n+a_{n-1}z^{n-1}+\cdots +a_0=0.$$
当次数 $n$ 只有几十时,MATLAB 的 `roots` 命令可以轻松应对;但当 $n$ 达到几千甚至上万时,传统方法(如友矩阵法)就会因 $O(n^3)$ 的计算复杂度和 $O(n^2)$ 的内存需求而寸步难行。更棘手的是病态问题,例如著名的 Wilkinson 多项式
$$W_{20}(x)=\prod_{k=1}^{20}(x-k),$$
即使系数只有极微小的舍入误差,也可能导致求根结果发生灾难性偏移。
能否同时实现“高效、鲁棒、完备”这三重目标?近期的研究给出了一套新的思路——通过分析多项式模方函数的几何与拓扑结构,把代数求根问题转化为一张"可被整体理解的地形图"。核心工具是一个几何对象——特征圆,以及在其上借助 FFT 进行的全局扫描。下面我们循着这一路径展开。
一、特征圆:穿过根群的"黄金截面"
把多项式的 $n$ 个根想象为复平面上的 $n$ 颗星星。根据韦达定理,它们有一个明确的“重心”,称为根中心:$c = -\frac{a_{n-1}}{n}.$ 更有趣的是根到该中心距离的几何平均值:
$$R_g = |f(c)|^{1/n} = \left(\prod_{k=1}^n |r_k - c|\right)^{1/n}.$$
以 $c$ 为圆心、$R_g$ 为半径作圆,就得到根系的一个特征圆。它的关键性质在于:这个圆并不把所有根包在内部,而是与根的平均分布区域发生结构性"接触"。
这种"穿过而非包围"的特性,使特征圆成为连接各个根吸引域的天然截面——就像一根绳子穿过一串珍珠,每一颗珍珠都在绳子上留下一个吸引域的入口。
二、模方拓扑:复平面上的"地形图"
定义模方函数 $F(z)=|f(z)|^2,$ 它在复平面上描绘出一张清晰的地形图:
- 深井:零点处 $F=0$,正是我们要寻找的目标;
- 高山:无穷远处 $F\to+\infty$;
- 山口:鞍点处 $f'(z)=0$ 且 $f(z)\neq0$,连接不同洼地的通道。
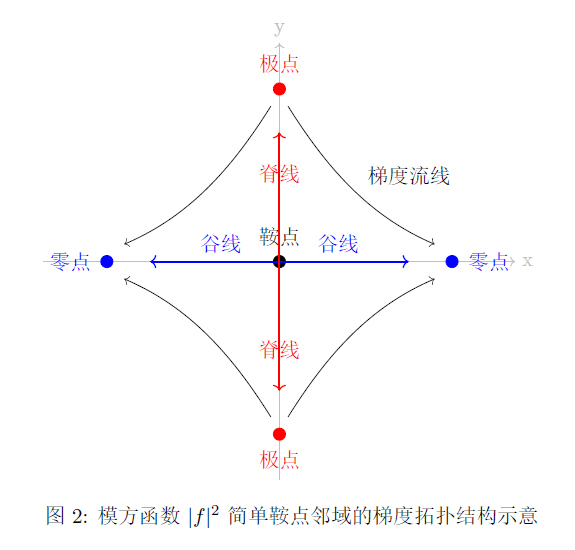
一个重要结论——沟谷连通性定理——表明:任意两个零点的局部洼地之间,都存在一条沿 $F$ 单调下降的连续路径(谷线)。所有谷线在鞍点处与上升的"脊线"相交,构成一张全局的联络图。
对多项式而言,脊线最终通向无穷远,相邻脊线围成的区域恰好包含一个零点,这个区域就是该零点的吸引域。特征圆穿过这些吸引域,在圆上留下一个个局部极小值点——它们正是通往各个根的"入口"。
这揭示了一个关键事实:多项式的根并非彼此孤立,而是被一张全局拓扑网络所约束。下图是多项式
$$ f(z)=(z-1)((z-6)^2+9)((z+2)^2+1)((z-1)^2+2+i) $$
的根系结构图
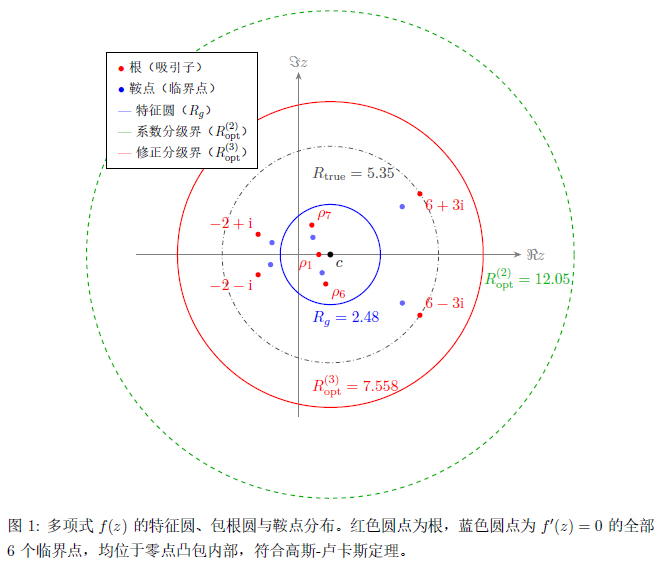
三、FFT 加速:从 52 秒到 71 毫秒
如何在特征圆上快速定位这些入口?答案来自傅里叶结构。在特征圆 $z=c+R_g e^{i\theta}$ 上,多项式的取值是一个有限阶三角多项式,其模方及梯度都可以通过一次 FFT 高效计算。具体流程是:
- 在圆上均匀采样 $M\approx 4n$ 个点;
- 用 FFT 同时计算 $F(\theta_j)$ 与切向导数 $\partial F/\partial\theta$;
- 通过导数符号变化精确定位极小值点;
- 结合径向梯度判断下降方向(指向零点)。
由此,初值构造的复杂度从 $O(n^2)$ 降至 $O(n\log n)$。在 $n=2000$ 的测试中,初值构造时间从传统 LSF 方法的 52 秒 降至 71 毫秒,加速超过 700 倍。
四、直径探测:破解方向性陷阱
特征圆并非没有盲区。当根分布具有强烈方向性(例如几乎全为实根)时,圆上的极小值点可能过少,难以覆盖所有吸引域。对此,我们引入直径傅里叶探测:
根据已发现的极小值点角度 $\varphi_k$,用最小二乘法拟合根分布的主方向
$$\theta_{\text{opt}}=\frac{1}{2}\arctan2\left(\sum \sin 2\varphi_k,\sum \cos 2\varphi_k\right),$$
然后沿该直径进行一维 FFT 搜索。必要时再补充一条正交直径,即可恢复完整覆盖。在 Wilkinson 多项式中,这一策略将根覆盖率从约 20% 提升到 100%。
五、实战检验:万次多项式并非神话
综合上述技术,我们形成了一套混合算法:
1. 初值构造:FFT-LSF + 直径探测($O(n\log n)$);
2. 预处理:少量梯度下降;
3. 精化:牛顿迭代至机器精度。
在随机多项式、病态多项式及 $n=2000$ 的大规模测试中,该方法保持了稳定的高成功率,并在内存占用上仅为 $O(n)$。相比之下,友矩阵法在 $n>1000$ 时已难以运行。此外,每个初值的后续迭代彼此独立,使该方法天然适合 GPU 并行。
六、展望:从多项式到黎曼猜想
这项工作的更深层意义,在于视角的转变:把"解方程"转化为对模方函数拓扑结构的分析。这一视角自然引向更一般的解析函数。以黎曼 $\zeta$ 函数为例,经典的 Speiser 定理表明:黎曼猜想等价于 $\zeta'(s)$ 在临界线右侧无零点。从几何角度看,这意味着零点分布与模方函数的鞍点结构存在内在关联。
我们的模方—鞍点分析框架,正提供了一种研究这种"零点—鞍点关系"的几何工具。若能在临界带内构造合适的几何截面,系统分析 $\xi(s)$ 模方的沟谷结构,或许能为理解黎曼猜想相关的几何机制提供新的线索。这仍是探索性的方向,但几何语言的潜力已经清晰可见。
结语 从特征圆的几何直觉,到 FFT 的高效实现,再到病态问题的鲁棒处理,我们为高次多项式求根提供了一条“可扩展、可证明、可实用”的路径。更重要的是,这项工作展示了一件常被忽略的事实:理解结构,往往比直接计算更重要。那些在复平面中穿行的沟谷,不只是数值算法的捷径,更是解析函数内在秩序的显影。也许,正是在这种理解中,数学最深的美感才得以显现。
本文基于论文《特征圆与模方拓扑:多项式求根的几何新视角》撰写,欢迎批评指正与深入讨论。
祝大家新春快乐,马年吉祥!
转载本文请联系原作者获取授权,同时请注明本文来自辜英求科学网博客。
链接地址:https://wap.sciencenet.cn/blog-239871-1522321.html?mobile=1
收藏

