转发中国科学院金属研究所网页新闻:
我国科学家确定背包问题计算复杂性下限
我国科学家在NP完全问题计算复杂性的研究方面取得重要进展。中国科学院金属研究所张志东研究员确定了背包问题的计算复杂度下限。论文发表在AIMS Mathematics 10 (2025) 11918-11938。
随着计算机领域的技术进步,人工智能正在影响我们日常生活的方方面面。而人工智能的进步依赖于计算算法的速度。如何在最短时间内算出正确的解是计算机领域科学家最关心的问题。NP完全问题是计算机科学中非常重要的难题。在计算复杂性理论中,NP表示非确定性多项式时间,NP问题定义为在一个非确定性图灵机上以多项式时间求解的决定性问题的集合。P问题是在确定性图灵机上以多项式时间求解的问题的集合。在NP中,以多项式时间确认解的决定性问题的集合归类为NP完全问题。在NP中所有其他问题都可以在多项式时间内约化为NP完全问题(以及其特例)。著名的NP完全问题有:布尔可满足性问题、旅行推销员问题、背包问题、哈密顿环问题、子集和问题、顶角覆盖问题、子图同构问题、独立集合问题、图着色问题、蛋白质折叠问题、自旋玻璃问题等。这一类非平凡难题的共同特征是具有随机性的模型系统中存在非平庸拓扑结构、非平面性图、非局域性或长程自旋纠缠。
针对N个具有固定权重和价值的二元变量的决定性问题,背包问题的目标是,在限制所有物体权重之和小于或者等于最大权重的前提下,最大化所有物体的价值之和。背包问题可以用来进行组合数学、密码学、商业等领域的计算,还可以应用在不同领域的决策,如寻找减少原材料使用、投资组合的选择、密钥产生等最优化搜寻路径。背包问题与自旋玻璃模型的联系:背包问题的二元决定性变量对应于自旋向上和自旋向下两种状态。背包问题的权重对应于自旋之间的相互作用。背包问题的哈密顿量可以映射成具有偏置场的自旋玻璃模型的哈密顿。所以,可以通过求解自旋玻璃模型求解背包问题。在背包问题中最大化所有物体的价值之和等价于在自旋玻璃模型中最小化自由能。
张志东首先分析了NP完全问题中非平庸拓扑结构的起源。从自旋玻璃三维伊辛模型出发,详细地阐明三维晶格上自旋排列与统计物理中转移矩阵的二维特征之间的矛盾导致非平庸拓扑结构。确认自旋玻璃三维伊辛模型存在绝对极小核心(AMC)模型,为一层晶格自旋玻璃伊辛模型与其最近邻层自旋的相互作用。它等于两层晶格自旋玻璃三维伊辛模型减去一个自旋玻璃二维伊辛模型。用蛮力搜索绝对极小核心模型决定了其计算复杂度的下限。并且,确认自旋玻璃三维伊辛模型中存在NP中间问题,给出体系的计算复杂度的相图。绝对极小核心模型存在于NP完全问题和NP中间问题的边界上。进一步地,根据自旋玻璃三维伊辛模型和背包问题之间的映射,证明背包问题同样存在绝对极小核心模型和NP中间问题,也给出背包问题的计算复杂度相图。并且证明了背包问题的计算复杂度的下限是亚指数、超多项式的。
本项工作通过物理思想做指导,分析体系的数学结构,提出一个判据,确定了NP完全问题的计算复杂度的下限为(1+无限小)的N次方。本项工作为NP完全问题的数值计算提供了指导性思维,例如通过发展绝对极小核心模型的平行计算,将会极大地优化算法,从目前的1.3的N次方提升至(1+无限小)的N次方。在保持一定计算精度的条件下,用亚指数算法获得复杂系统(如自旋玻璃三维伊辛模型、背包问题等)的精确结果。
本项工作建立了背包问题与自旋玻璃三维伊辛模型的联系,根据两个问题的关系确定了背包问题的计算复杂度的下限。背包问题可以被映射为许多其它的科学问题,所以本项工作的结论可以直接推广应用,解决计算机、物理、化学、生物、数学以及材料科学领域一系列相关基础科学问题。
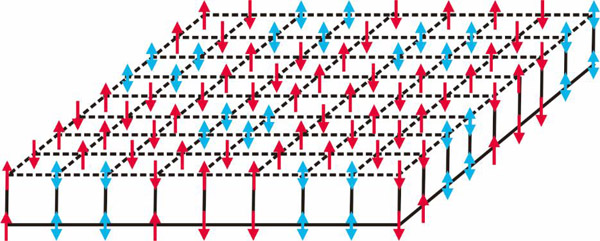
图1.自旋玻璃三维伊辛模型最小核模型示意图,其中红色自旋指向随机分布,并且蓝色自旋存在阻错。
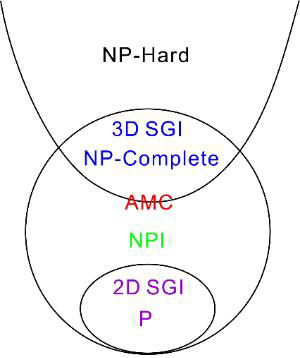
图2. 自旋玻璃三维伊辛模型体系计算度的相图。其中NP中间问题(NPI)在NP完全问题与P问题之间,绝对最小核(AMC)模型在NP完全问题与NP中间问题的边界上。
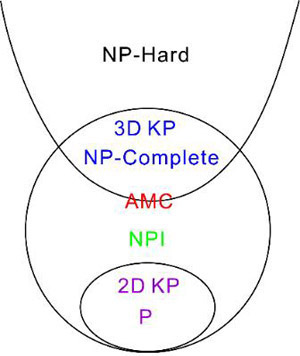
图3. 背包问题计算度的相图。其中NP中间问题(NPI)在NP完全问题与P问题之间,绝对最小核(AMC)模型在NP完全问题与NP中间问题的边界上。
转载本文请联系原作者获取授权,同时请注明本文来自张志东科学网博客。
链接地址:https://wap.sciencenet.cn/blog-2344-1487491.html?mobile=1
收藏

