16.12 唯一解
GPT5迟迟未发布,很多人心存疑虑,通用人工智能只是海市蜃楼?AI知识图谱没有理论依据?深度学习黑箱全靠瞎蒙?AGI俨然根本就不可能实现?
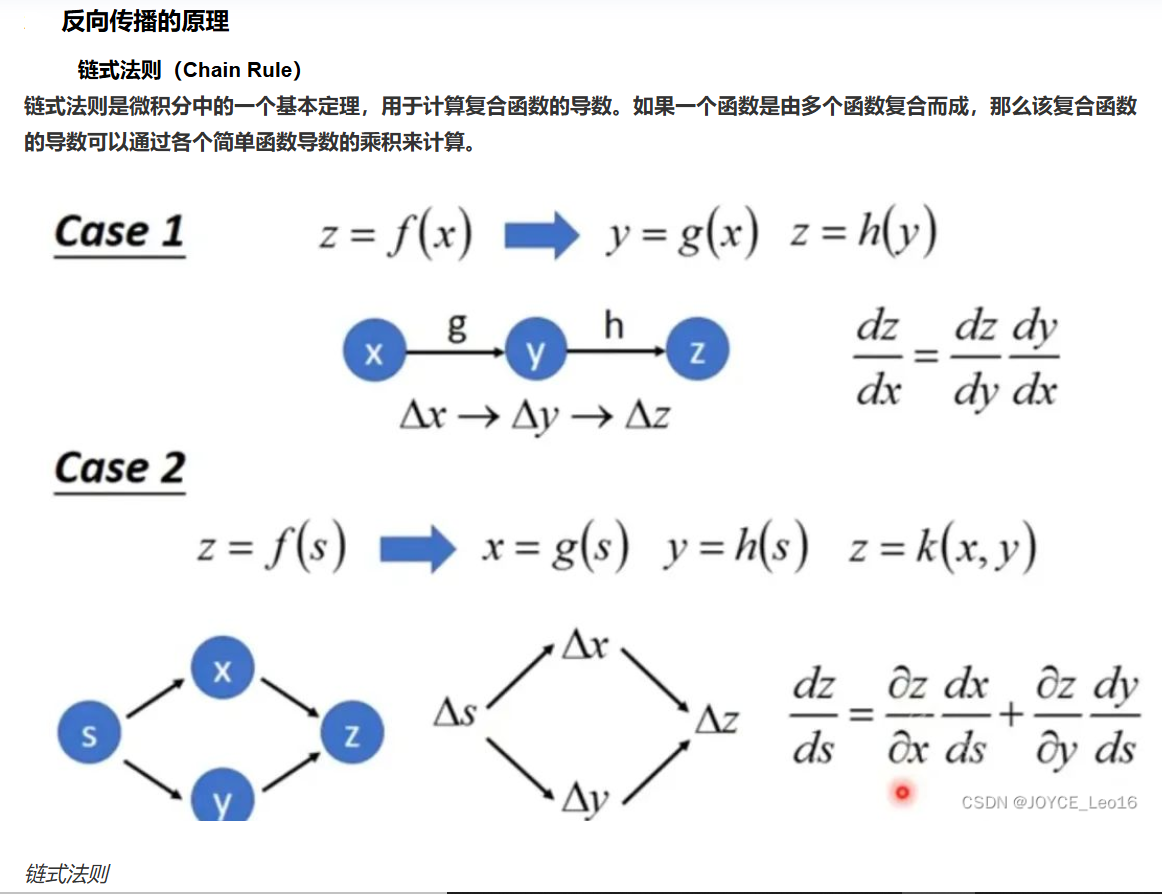
最关键的问题:普适意义下的深度学习核心算法反向传播复合函数一定会有解吗?
伯原正树给出了答案!

2025阿贝尔奖公布78岁的日本京都大学教授柏原正树荣获此大奖,以表彰其“重塑数学边界”,对代数分析和表示论领域做出的基础贡献。模理论连接了表示论、代数几何与微分方程等多个数学领域,特别是伯原正树的D-模(D-modules)理论证明了线性微分方程的唯一解。
通过将群或李代数的表示转化为线性算子,D-模为表示论提供了新工具,D-模与多项式函数有限性的紧密关系,D-模的几何性质(如奇点分布)可通过代数簇或层论研究,而微分方程的解空间则对应D-模的截面。D-模理论通过代数语言将微分算子的作用形式化,使得复杂方程的求解可转化为模论中的操作,极大扩展了数学工具的应用范围。为量子群的表示理论提供了组合框架。大环论证等创新方法成为解决无限维问题的典范。
‘D模中’的D指微分算子Differential、模是环上的模结构。
如果我们把函数看作矢量、微分算子环视为实数域,D模就如同线性空间,微分方程的解视同D模代数表示空间的投影值。
伽罗瓦定理将群与特征属性对应,一个不变子群可以找到一个不变子特征空间与之对应,反之亦然。将多项式方程的特征解,对应到线性空间基矢量(一阶特征基)的特征值。
域扩张L/K可视为L作为K-线性空间的扩张。此时,L的维数称为扩张次数[L:K],由基矢量增加的个数决定。例如,单扩张K(α)的基由α 的最小多项式次数决定。此处一阶特征元的特征扩张可理解为代数元添加基矢量导致的线性空间的基维数扩张,扩张次数即为基的维数(域扩张 [M:L][L:K] = [M:K])
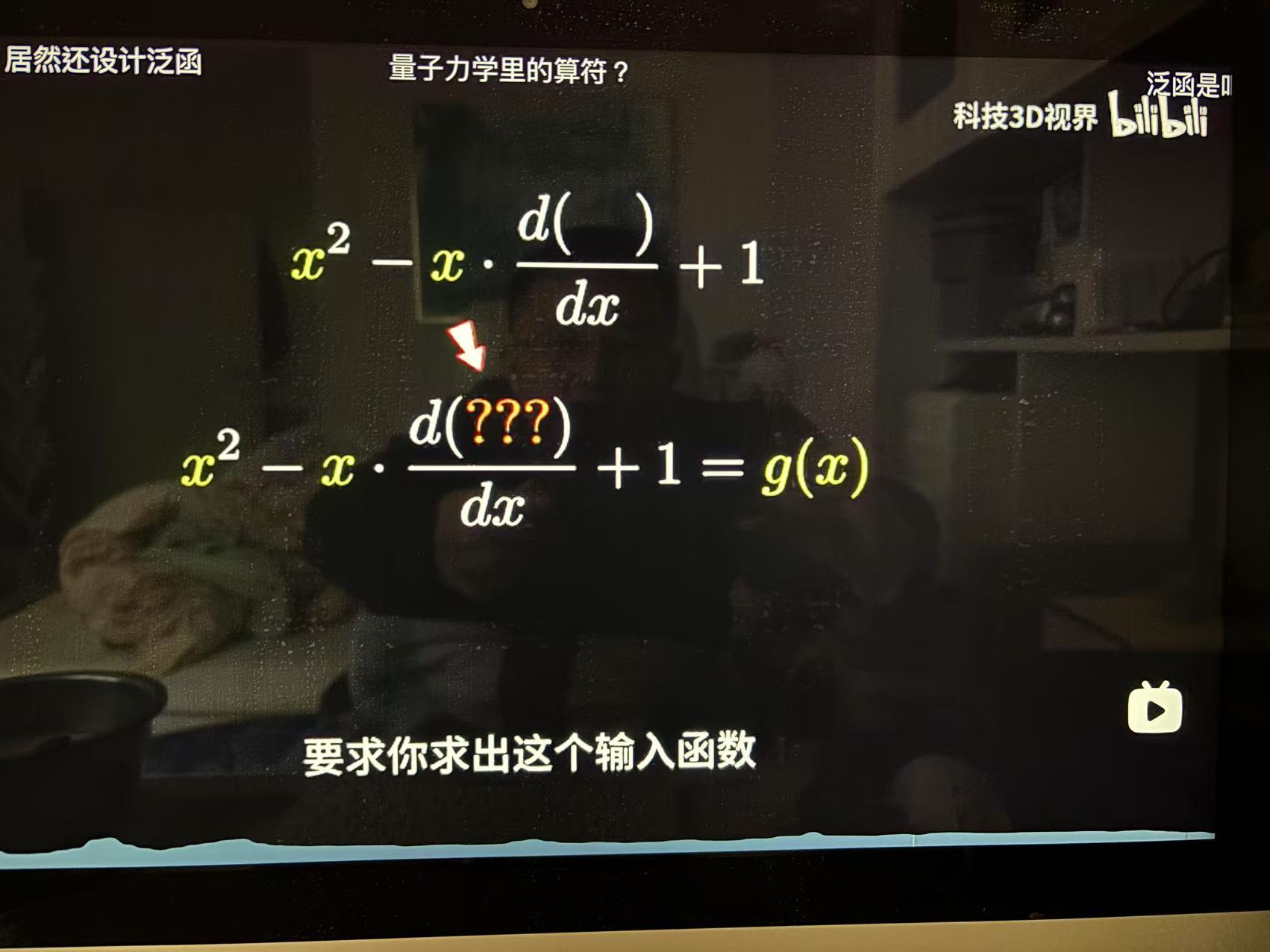
但是仅仅维数扩张的参照系,其代数空间表达是不够的,无法得出普适意义下复合函数是否有解的结论。比如,在坐标r表象中动量p等于(-id/dr),动量p是位移r的函数,实数空间中动量p对于位移r是不确定的,换句话说实数域p对于r无解。
本文核心观点,正如有理数(阿列夫0维度)无法极限逼进无理数(阿列夫1维度),连续无穷维谱分析线性空间(阿列夫1维度特征)无法表达高阶张量(阿列夫2维度的)。事实上,阿列夫2维度的exp(ipr)特征基代数系统超出线性空间表达阈值,它并不是线性空间。参阅《关于不完备性定理和不确定性原理的探讨 (小结)》
我们知道,exp(ipr)是所有线性时不变系统的共同本征函数(特征基)系。 参阅《关于不完备性定理和不确定性原理的探讨(五)(6)》
请注意,线性时不变系统的系数a0、a1......an,b0、b1、......bm均为不随时间变化的常数:
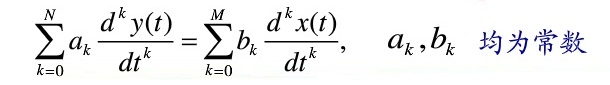
进一步看,如果上式的系数不是常系数、而是变量,甚至不是标量、而是矢量,那么上式就会成为多个矢量乘积复合的复杂程度倍增的高阶张量方程。
复合特征的高阶张量对我们人类而言,是非常难以理解的,往往匪夷所思。比如,桌子加椅子我们知道是一套餐具,但是桌子乘以椅子的复合体是什么玩意呢?
‘桌子*椅子’这样的二阶体元的复合特征属性可以数学表达吗?
上面提到过,线性空间概念的扩展,是更宽泛的“模”的概念。
如果说当今数学空间有什么放之四海而皆准的大一统表达,那么这个表达系统就是“模”
交换群、环、线性空间等都只是模结构的特例而已:
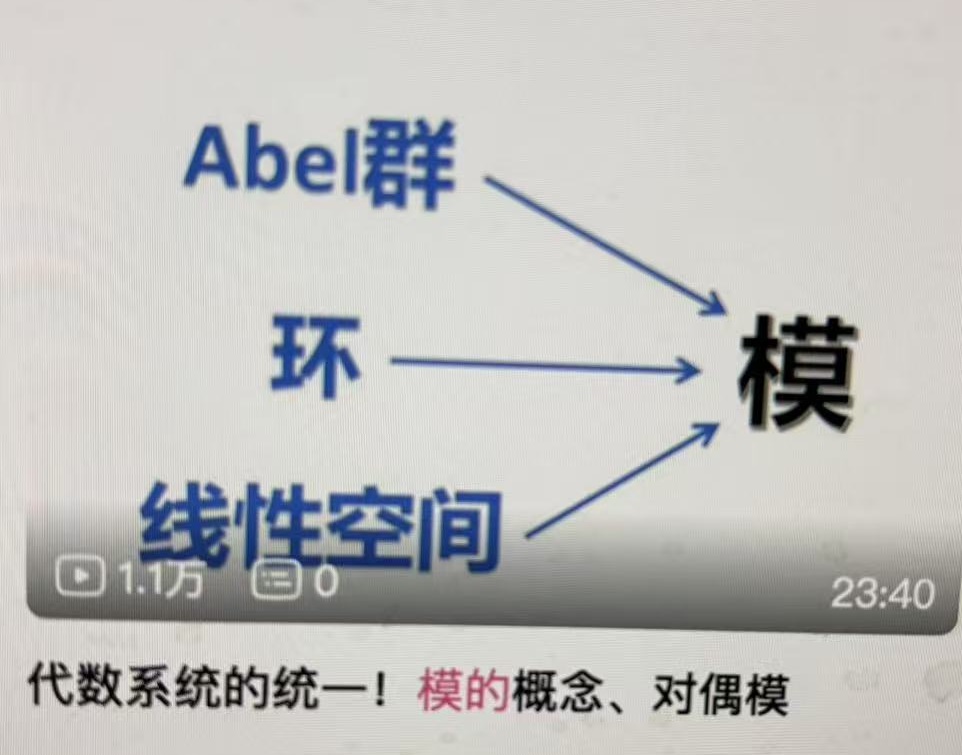
环上的模概念是对于域上的向量空间概念的推广,环(R,+,*)作用交换群(M, +)的算子 R× M→ M称为左R-模。
备注:模结构要求交换群(避免不确定性原理的不对易性缺损)。参阅《关于不完备性定理和不确定性原理的探讨(十六)(8)》
线性空间的域都是数域(标量),线性空间的矢量只可以相加不可以相乘,因此线性空间的特征元都是一阶特征属性的;
环中的特征元不限于标量,环中的特征元可以相加也可以相乘(高阶复合),因此模空间的特征元可以是高阶特征属性的。
规范子群作用进行扩域,数域扩张为线性空间;理想作用进行扩环,环扩张为模结构。域扩张和环扩张在结构上存在显著差异,主要源于它们各自的代数性质及所涉及的特征属性结构。域扩张是线性空间特征基(特征值)的扩张,是一阶特征元个数的扩张;环扩张是模上的特征元(特征属性)的扩张,不仅仅是特征元个数的加法扩张,同时也是特征复合阶数的乘法扩张。
环扩张S/R中,S作为R-模的结构更为复杂。若S是有限生成R-模,其生成元可能需满足非平凡关系(如理想约束),导致模结构可能非自由(存在挠元)或需多生成元。此时扩张不仅涉及生成元数量(类似基的个数),还需考虑环作用下生成元的复合关系(如乘法封闭性、模的合成列等)。若环扩张涉及非平坦模(如含扭结构),则需更复杂的生成元关系,体现“复合阶数”的扩张。环扩张中模的生成元或代数作用下的元素(特征元),其复合可能涉及环运算的多重嵌套(如多项式关系)。环扩张中需同时处理生成元数量及环作用复合,复合阶数指模结构中生成元的环作用的复合结构(如关系式、挠、合成列长度),需同时考虑生成元数量的维数加法及运算层次的阶数乘法。
很显然,模结构表达客观世界,比线性空间表达更具普适意义。事实上,AI深度学习模型的多隐层结构多特征元结构即是一种模结构,高阶特征元表达的深度学习参数集就是泛化特征解概念。AI工程师坚信只要不断增加深度学习隐层和特征元,也就是不断进行环扩张,总能构建完备表达宇宙全景知识图谱的模结构。假若模同态存在普适的最优解,那么显而易见深度学习模式的通用人工智能路径就是正确的。
是这样吗?
回到终极问题,特征维数和特征阶数的同时扩张得到的模结构表达空间,是否始终能获取最优解,放之四海而皆准?
深度学习模型矩阵乘积如同线性算子,深度学习不断添加隐层和特征元如同线性微分算子D模的环扩张。
线性微分方程的解空间转化为代数对象特征空间,代数方程是否有解相当于D模是否完备。伯原正树证明了这个关键梗。
D模有唯一解的更重要意义在于,同时也证明了深度学习模型的辛顿反向传播算法普适意义下有解且有唯一解!!!
上一节我们学习过,黎曼zeta函数通过复域空间延拓,把无解的无穷加转换为有解收敛值,从而扩展了欧拉乘积公式的深刻内涵。同样的,伯原正树证明,模扩张能把暂时无解的大模型扩展为有解的普适AGI,这个意义更加深刻。
转载本文请联系原作者获取授权,同时请注明本文来自陈正茂科学网博客。
链接地址:https://wap.sciencenet.cn/blog-1666470-1483505.html?mobile=1
收藏

