[笔记,数学] 泰勒级数展开 Taylor series expansion
一、一元实变量 One real variable
https://mathworld.wolfram.com/TaylorSeries.html
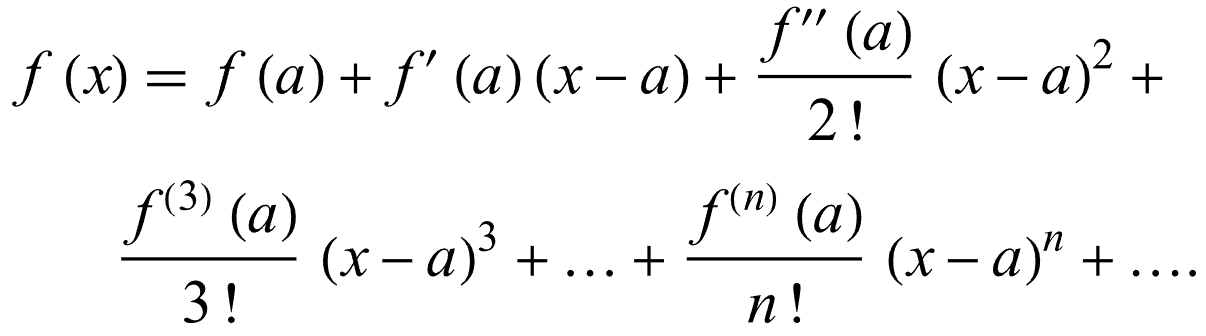
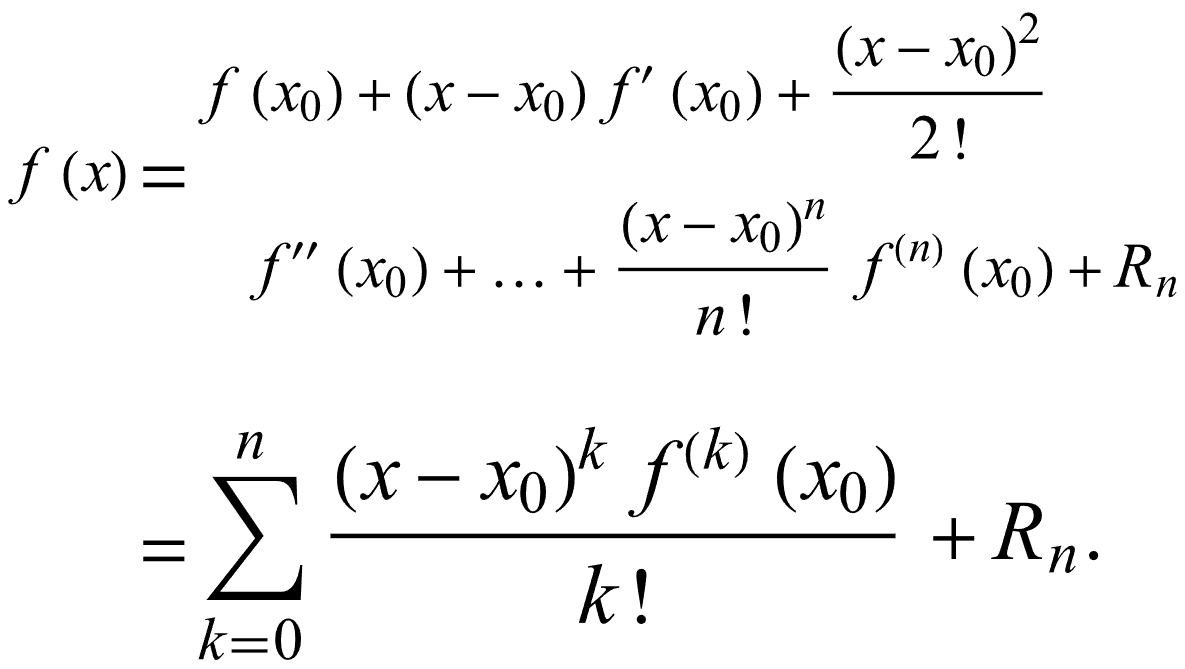
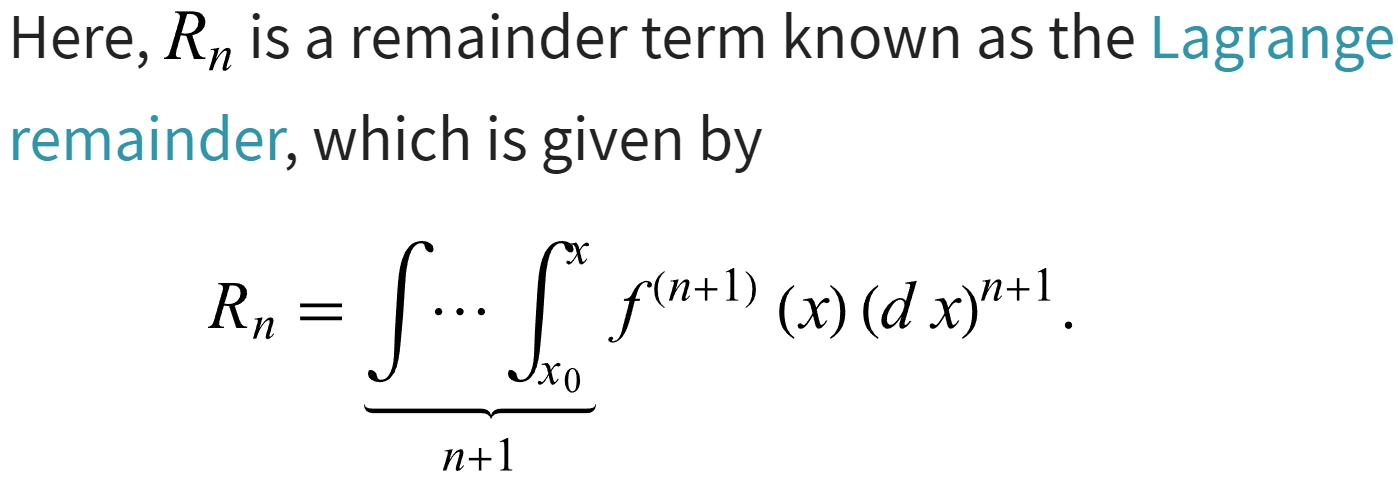
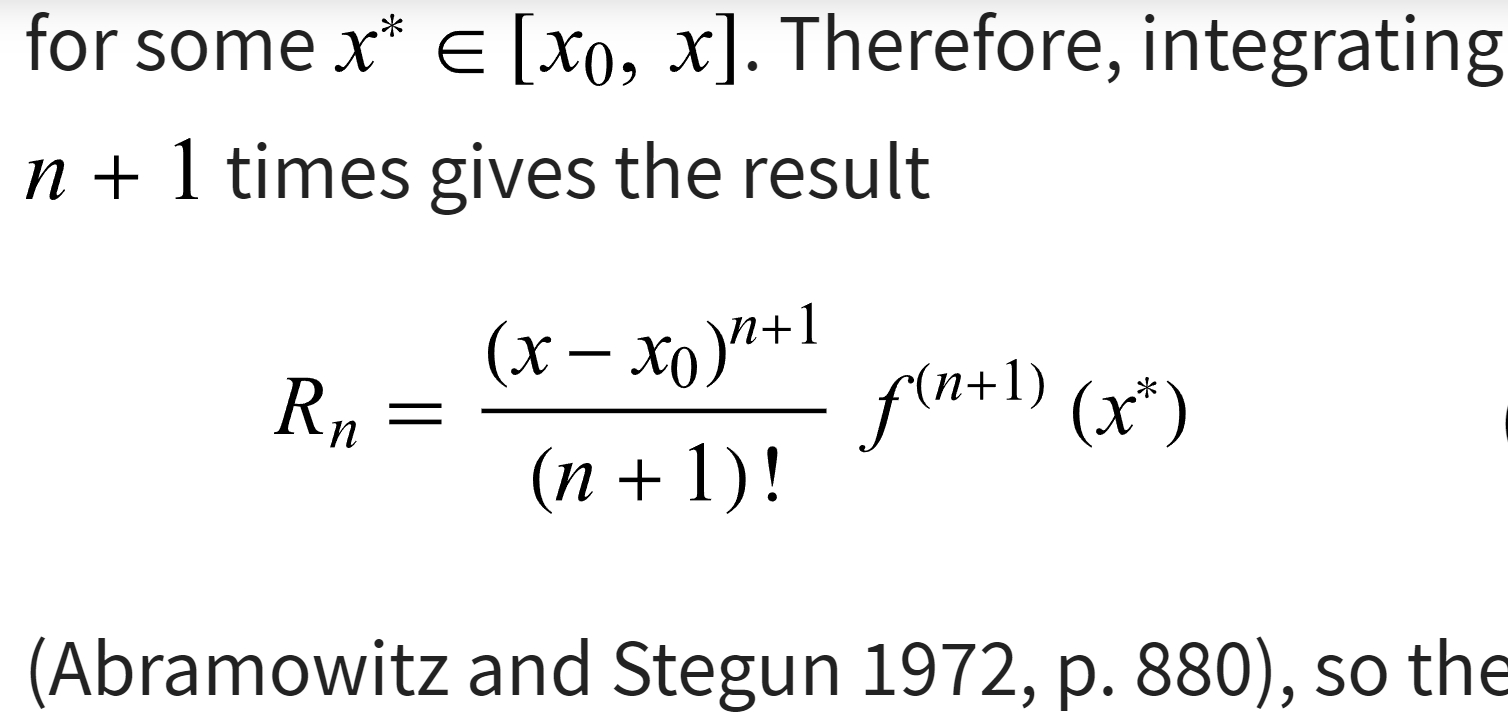
二、多元实变量 Several variables
https://mathworld.wolfram.com/TaylorSeries.html
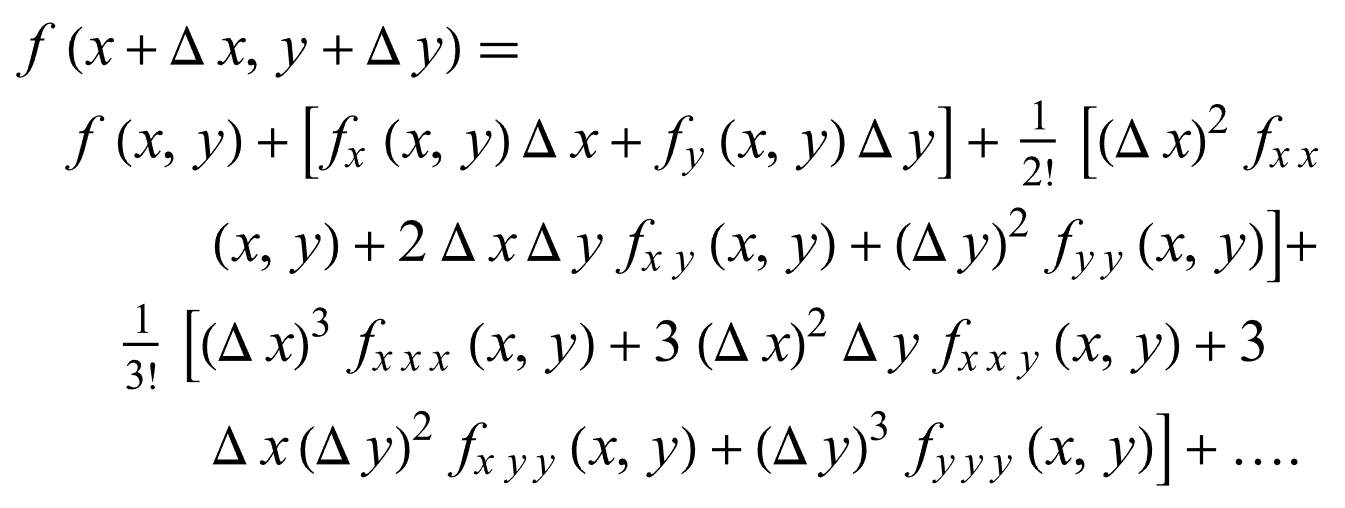
三、多元泰勒展开:拉格朗日余项 Lagrange remainder 的公式是什么?
参考资料:
[1] 2022-01-20,泰勒级数/Taylor series/张南岳,中国大百科全书,第三版网络版[DB/OL]
https://www.zgbk.com/ecph/words?SiteID=1&ID=112591&Type=bkzyb&SubID=99584
[2] 2024-08-24,生命周期不确定性分析/uncertainty analysis of life cycle assessment/洪静兰,中国大百科全书,第三版网络版[DB/OL]
https://www.zgbk.com/ecph/words?SiteID=1&ID=117455&Type=bkzyb&SubID=102323
[3] Weisstein, Eric W. "Taylor Series." From MathWorld--A Wolfram Web Resource.
https://mathworld.wolfram.com/TaylorSeries.html
[4] Weisstein, Eric W. "Lagrange Remainder." From MathWorld--A Wolfram Web Resource.
https://mathworld.wolfram.com/LagrangeRemainder.html
[5] Taylor formula. Encyclopedia of Mathematics.
https://encyclopediaofmath.org/wiki/Taylor_formula
[6] Taylor polynomial. Encyclopedia of Mathematics.
https://encyclopediaofmath.org/wiki/Taylor_polynomial
[7] Taylor series. Encyclopedia of Mathematics.
https://encyclopediaofmath.org/wiki/Taylor_series
[8] Taylor Series, Brilliant Math & Science Wiki
https://brilliant.org/wiki/taylor-series/
相关链接:
[1] 2022-03-24 17:13,[打听] 傅里叶级数展开的余项(remainder term, Fourier series)
https://blog.sciencenet.cn/blog-107667-1330860.html
[2] 2020-10-11 14:31,[备课] 狄里赫利条件 Dirichlet conditions 汇集
https://blog.sciencenet.cn/blog-107667-1253975.html
[3] 2023-07-14 01:22,“电磁学的实验再检验”:经典电磁学实验当代再检验的起因、意义要点
https://blog.sciencenet.cn/blog-107667-1395251.html
[4] 2025-04-21 22:49,[权威,观点,汇集] 传统的同行评审(同行评议):它消极对待真正的创新思想,拒绝领域内具革命性的文章
https://blog.sciencenet.cn/blog-107667-1482882.html
[5] 2023-10-26 22:44,[最主流,实体的物理实验波形] “费曼电容器充电”的电压波形观察
https://blog.sciencenet.cn/blog-107667-1407363.html
[6] 2024-07-01 22:49,[专业微信群贴出] 请教安培的无定向秤( astatic balance )的系统误差
https://blog.sciencenet.cn/blog-107667-1440567.html
感谢您的指教!
感谢您指正以上任何错误!
感谢您提供更多的相关资料!
转载本文请联系原作者获取授权,同时请注明本文来自杨正瓴科学网博客。
链接地址:https://wap.sciencenet.cn/blog-107667-1485748.html?mobile=1
收藏

