博文
穿越欧氏空间与非欧空间
|
欧氏即欧几里得(Euclid,约前325-前270),其英文名Euclid是希腊名 Εὐκλείδης的英文化版本,意思是“著名的、光荣的”。欧几里得就像他的名字一样,在人类历史的长河中,成为了一颗璀璨的明星。欧几里得的《几何原本》(Element, 基本原理之意)以5个公理和5个公设基础,将他之前的数学命题采用形式逻辑的方式明白无误的一一推演出来,形成了数学的公理化体系,揭示了数学大厦的精巧与雄壮的同时,也让人们看到纷繁世界的简洁性。
《几何原本》的5个公理和5个公设分别如下:
(5个公理)
1) 等同于一个量的两个量相等;
2) 等量相加,其和相等;
3) 等量相减,其差相等;
4) 可以重合的图形,对应的量相等;
5) 全体大于部分;
(5个公设)
1) 两点之间可以作一条直线段;
2) 直线段可以无限延长;
3) 以任意一点为中心、以任意给定的线段为半径可以作一个圆;
4) 所有的直角都相等;
5) 若一条直线段与另外两条直线段相交,且一侧的内角之和小于两个直角,则该两条直线段无限延长后必相交。
所谓的公理化体系,是指在《几何原本》13卷中的467个命题,全部可以由5个公理和5个公设导出,或者由它们导出的定理导出。换句话说,有了这5个公理和5个公设,就可以得到整个数学大厦。爱因斯坦曾高度赞赏了《几何原本》严密的公理化体系,他说:
“在逻辑推理上的这种令人惊叹的胜利,使人们为人类未来的成就获得了必要的信心。”
《几何原本》的公理化体系也成为后世许多著名科学家争相效仿的榜样,如牛顿就以牛顿三大力学定律为基本原理,构建了牛顿力学体系;此外,现代政治学创世人Thomas Hobbes(霍布斯,1588-1679),哲学家Baruch Spinoza(斯宾塞,1632-1677),博学家Bertrand Russell(罗素,1872-1970),经济学家Ludwig von Mises(第四强度米塞斯的哥哥,1881-1973)等都曾采用公理化的演绎结构为自己的理论创建基本原理(element)。
然而,美中不足的是欧几里得第5公设,如图1所示,根据第5公设,可知:当线1与线2和3相交,其一侧的两个角度相加小于两个直角之和,则线2和3相交。与前4个公设相比,第5公设在描述上略显繁琐,读起来更像是一个定理,而非公设。因此,许多数学家认为第5公设可能不独立于前4个公设,并尝试由前4个公设导出第5公设。
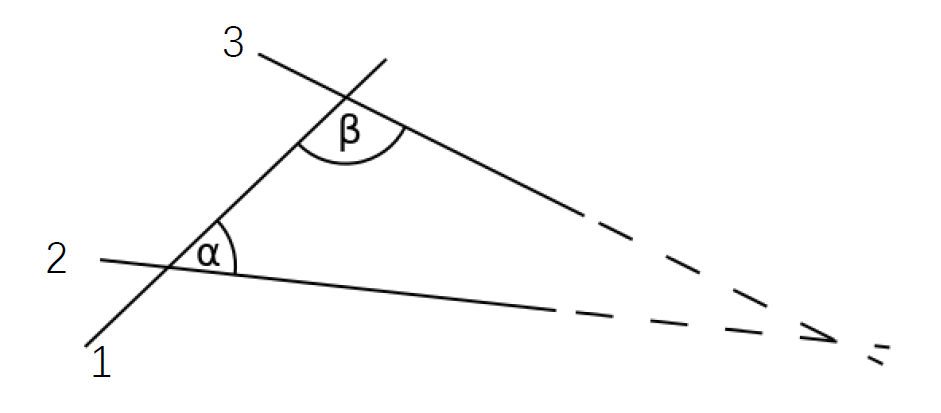
图1 几何原本第5公设示意图
但令人遗憾的是,许多声称自己证明了第5公设的数学家后来都被证明他们采用了与第5公设等价的命题,因此证明也是无效的。这其中也包括古希腊天文学家托勒密(Ptolemy, 约100-约170),苏格兰数学家普莱费尔(John Playfair,1748-1819)指出,托勒密的证明用到了平行公设,而平行公设与第5公设是完全等价的,平行公设现在被描述为:
过给定直线外一点,可以作一条直线并且只能作一条直线,与已知直线平行。
证明第5公设的工作是旷日持久的,延续了2000多年,但他们无一例外的均以失败告终。但这些失败也非完全没有收获,人们得到了一系列的与第5公设等价的命题,其中的两个命题是这样:
1) 三角形的内角和等于180度(与平行公设等价);
2) 有矩形存在(与平行公设等价)。
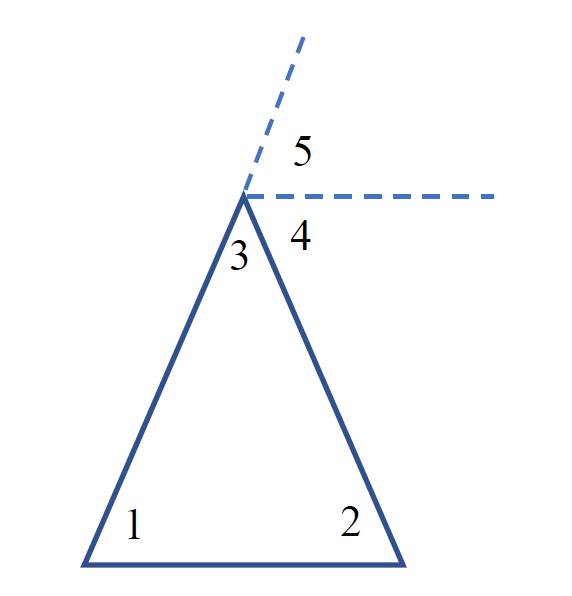
图2 三角形内角和为180度等价于平行公设
著名的法国数学家勒让德(Adrien-Marie Legendre,1752-1833)曾导出“若三角形内角和等于180度,则平行公设成立;若小于180度,则平行公设不成立。”我们不禁想问,有内角之和小于180度的三角形吗?
这可以利用萨开里四边形来证明,萨开里(Giovanni Girolamo Sacceri,1667-1733)是17世纪意大利数学家,萨开里四边形假设四边形有两个直角,而另外两个有三种可能:锐角、直角和钝角。如图3所示四边形,设∠A=∠B为直角90度,AD=BC。在不使用第5公设的前提下即可证明∠D=∠C,这时∠D和∠C的取值有三种可能:
1)∠D=∠C,都小于直角(锐角假设)
2)∠D=∠C,都等于直角(直角假设)
3)∠D=∠C,都大于直角(钝角假设)
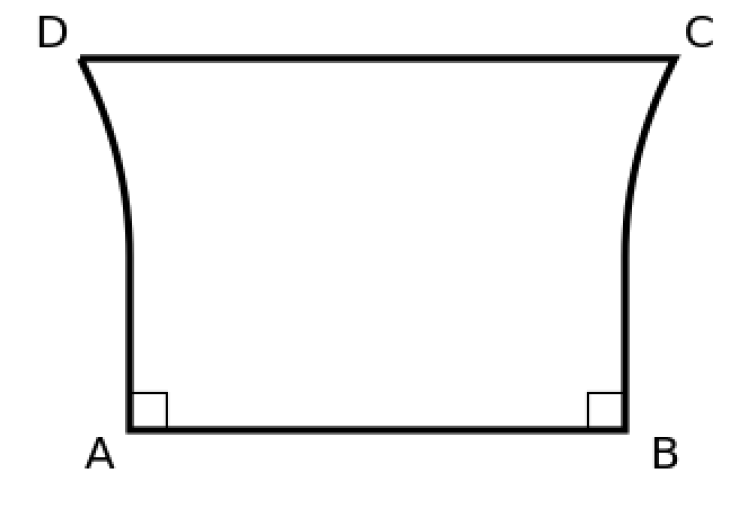
图3 萨开里四边形
如图4所示,我们假定△ABC为已知三角形,D、E是它两条边上的中点,过D、E作直线l。过A点作l的垂线,垂足为F。在l上作G和H两点,使得GD=DF,HE=EF。这样,可以导出两对全等三角形:
1)由于∠ADF=∠BDG(对顶角),AD=DB(D是AB中点),又GD=DF
所以,△ADF全等于△BDG。
2)由于∠AEF=∠CEH(对顶角),AE=EC(E是AC中点),又HE=EF
所以,△AEF全等于△CEH。
由这两对全等三角形可知,有∠GBD=∠DAF和∠HCE=∠EAF,因此,萨开里四边形中∠GBC和∠HCB之和就是三角形的内角和。如果我们采用了萨开里锐角假设,则三角形内角和小于180度时;如果采用直角假设,则三角形内角和等于180度;如果采用钝角假设,则三角形内角和大于180度。
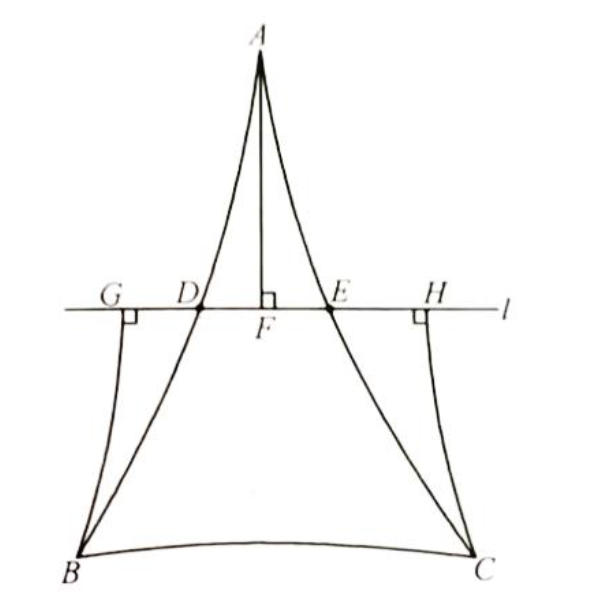
图4 三角形内角和小于180度
第5公设(或平行公设)告诉我们,一条线与两条线相交,其一侧的内角和小于180度时,两条线延长后相交。但是在萨开里四边形中,却出现了相反的情况,如图4所示,AD与AB和DC相交,其一侧的两个内角之和∠D+∠A显然小于180度,但CD却平行于AB。这说明“当一条线与两条线相交,其一侧的内角和小于180时,两条线也可能成为平行线”。这样,萨开里就在锐角假设下,导出了“过线外一点可以有多条直线与已知直线平行”的结论。进一步更证明,过直线外一点若可以作两条平行直线的化,则夹在两条直线之间的直线都平行于已知直线,也就是说在这种情况下过直线外一点,可以作无数多条直线与已知直线平行。
萨开里得到这一结论时,认为这是如此的荒谬,因此他更加坚定了自己欧几里得信仰,并于1733年出版了一本书《欧几里得几何无懈可击》。然而,萨开里在锐角假设下导出的现象只是与人们的直观感受矛盾,并没有逻辑上的矛盾。这使得人们对第五公设能否证明产生了怀疑。与其不厌其烦的去证明第5公设,倒不如思考承认萨开里锐角假设、钝角假设和直角假设一样,都可以作为第5公设构建新的几何体系。
最早这样尝试的是大数学家高斯(Johann Carl Friedrich,1777-1855)。1792年,高斯试图以萨开里四边形的锐角假设更换欧几里得的第5公设(平行公设),并建立一种新的逻辑几何学。1794年高斯在写给好友的信中指出,在这种几何中,三角形的内角和小于180度,而且面积依赖于内角和、而不依赖于边长和高。他给这种几何起名为反欧几何(后来称非欧几何)。但高斯深知这样做的风险极大,因为担心发表这些结果会遭致“黄蜂绕耳”的攻击,高斯选择不发表他的发现。
30年后的1826年,俄国数学家罗巴切夫斯基(Nikolai Lobachevsky,1792-1856)首次公开了他的研究成果,即以萨开里四边形的锐角假设替换欧几里得第5公设创建了一种新几何体系,当时他将其称为“想象中的几何”,从1829年开始,罗巴切夫斯基发表了一系列的有关非欧几何的学术论文,这就是后来被认为称为罗氏几何的来源。现在我们为罗巴切夫斯基感到荣幸,但在当时他却遭受了各种不公正的待遇,在孤独中度过了他的晚年。后来人们发现高斯生前曾做过与他相同的研究,才对罗巴切夫斯基的工作开始重视并进一步的研究。
前面已经可以看出,从萨开里四边形出发,有三种可能,即锐角假设(导出三角形内角和小于180度)、钝角假设(导出三角形内角和大于180度)和直角假设(三角形内角和等于180度)。直角假设导出的就是欧氏几何,锐角假设导出的就是罗氏几何,很显然还有一种钝角假设。从钝角假设出发,构建新几何体系的是德国数学家黎曼(Georg Friedrich Bernhard Riemann,1826-1866)。
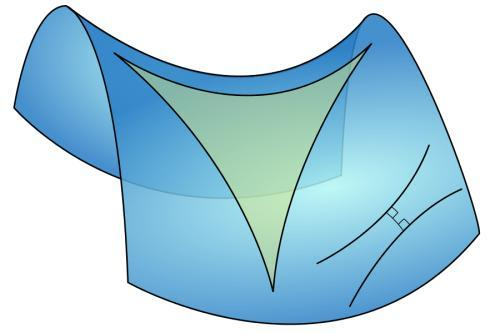
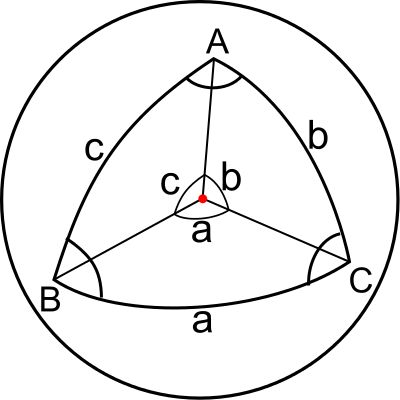
图5 双曲面上三角形内角和小于180度,球面上三角形内角和大于180度
我们知道罗氏几何是在锐角假设下构建的,相当于欧氏几何体系中的第5公设(平行公设)更换为“过已知直线外一点可以作无数条直线与已知直线平行。” 相反,在黎曼的非欧几何体系中,相当于欧氏几何中的第5公设(平行公设)更换为“过已知直线外一点不能作任何一条直线与已知直线平行。”
可能,在你看到这些描述时仍然觉得的不可思议,没关系,我们可以做这样一个尝试。假设你在纸上画出两条平行线,假想它们可以无限延长,纸的面积太小,我们直接画在大地上,为了方便描述,我们画两条南北走向的线,然后无限延长它,穿过城市、穿越国境线,无限延长的结果就是你发现当到达北极或南极时,它们都相交了。

图6 球面上过线外一点作不出平行线(如所有经线都相交)
这就是“过直线外一点,无法作一条直线与已知直线平行”,我们所谓的平行,只是在相对小的范围内成立,当我们放大视野后,会发现在球面上做不出平行线,黎曼所构建的几何正是在球面上的几何。另外一种非欧几何,罗巴切夫斯基非欧几何被兰伯特(Johann Heinrich Lambert, 1728-1777)预测是发生在半径为虚数的球面上的几何,后来被证实。
后来,人们将欧氏几何(直角假设)、罗巴切夫斯基的非欧几何(锐角假设)、黎曼的非欧几何(钝角假设)统称为黎曼几何,三种假设下的几何体系就成为了黎曼几何的特例:欧几里得几何所对应的曲率为0的空间;黎曼的非欧几何对应的是曲率为正常数的空间(如球面);而罗巴切夫斯基的非欧几何所对应的是曲率为负常数的空间(如双曲面)。
这样,弯曲的空间出现了,黎曼几何为爱因斯坦的相对论提供了有效的数学基础,在黎曼几何下弯曲的时空观出现了。
说明:本文主要参考了李忠《并不神秘的非欧几何》,高等教育出版社。
https://wap.sciencenet.cn/blog-847068-1326218.html
上一篇:专业思政的意义与实现途径
下一篇:三角函数的诞生与发展
全部作者的精选博文
- • 熵在自我管理中的启示
- • 马太效应的力学原理
- • 力学与柏拉图的理念世界
- • 科氏力实际是科里奥利力
- • 力学就业与段誉爱情的相似性
- • 力学研究方法之凌波微步