本文作为论文Path Planning Using Lazy PRM的阅读笔记。
        这篇论文的意义是重大的，因为它明确提出了利用延迟碰撞检测的办法来减少不必要的碰撞检测次数从而提高规划效率的Lasy思想。这个思想被后人使用了n多次，而这篇，正是Lazy始祖。
        首先，这篇文章的算法是为单查询任务设计的（也能用于多查询任务，后面会解释）。单查询规划器有个基本要求：快！为何？试想，多查询规划器，比如说经典PRM，建一幅地图可以反复利用，那么，即使它构建地图速度稍慢，也还是可以容忍的。而单查询规划器，本来就是“一次性”的，地图用完一次即作废，如果速度再那么慢，可谓“两头都不占”，必然遭人鄙视。
        论文的中心思想就是尽量减少 调用局部规划器（local planner）的次数，从而获得较快的规划速度。显然，减少调用局部规划器的次数，说白了就是减少不必要的碰撞检测。
        首先看一下算法流程图：

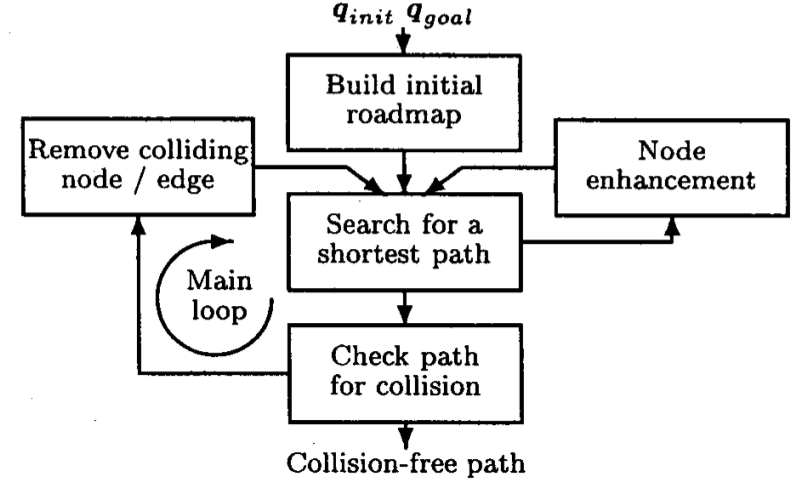
        先看Build initial roadmap。给定两个查询位姿$q_{init},q_{goal}$ 和一个采样点个数$N_{init}$，然后随机均匀采样。采样的同时，会涉及到邻域选取的问题，因为每当一个采样点被加到地图上，它都要立刻和它邻域中的点相连，这样，当$N_{init}$个采样点都被加入地图的时候，一幅真正的、包含点和边的地图也就形成了。为什么当前采样点只和它邻域中的采样点相连呢？第一，如果把当前采样点和已经加到地图中的每个采样点相连，会产生大量的边从而耗费很大内存；第二，如果两个采样点离得较远，它们之间很可能有障碍物，尝试用直线路径相连很可能会失败。上述两点可以认为是“出力不讨好”。明白了邻域的重要性，我们来看怎样选择邻域。论文选择了一种尺度$\rho_{coll}:C \times C \rightarrow [0,+ \infty)$ 来衡量距离。这个距离应该反映出用无碰撞的直线路径连接两个采样点的难度，即距离越大，存在直线路径的概率越小。由于该论文主要解决机械臂问题，而机械臂底部移动一个单位比它的末端移动一个单位更容易产生碰撞。因此，作者采用一种加权欧式距离：$\rho_{coll} \left (x,y \right )= \left (\sum\limits_{i=1}^{d} w_{i}^{2}\left (x_{i}-y_{i} \right )^{2} \right )^{1/2}= \left (\left (\textbf{x-y} \right )^{\textbf{T}}W \left (\textbf{x-y} \right ) \right )^{1/2}$ 。 其中d是C-Space的维数，$W=diag \left (w_{1}^{2}, \cdots, w_{d}^{2} \right )$ ，$\textbf{x}^\textbf{T}$ 是$\textbf{x}$ 的转置矩阵。这些权值正比于当机器人在C-Space中沿着相应的坐标轴移动一个单位时，机器人上的点在工作空间（workspace）中移动的最大可能欧式距离。乍一看，Build initial roadmap貌似和经典PRM的地图构建很相似；再仔细一想——不对啊，经典PRM在连接当前采样点和它邻域中的采样点时调用了碰撞检测函数啊，这里怎么没有？That's the point! Let's go on!
        其实，这恰恰是Lazy PRM的特色所在——延迟碰撞检测。不仅延迟边的碰撞检测，而且延迟点的碰撞检测——难道你没有发现，在Build initial roadmap中根本就没有提到自由空间F吗？在经典PRM的地图构建步骤中，每采样一个点，必先检查其是否位于自由空间F中，之后又要检查它与邻域中的点是否可用直线路径相连。然而，在Lazy PRM中，这些碰撞检测被延迟了。不是不检测，时候未到而已。这恰好体现了单查询的特点，即此时构建的地图以及基于此地图查找的路径是无法复用的，因为这个地图本身就可能不“合法”，于是这条路径也可能是有碰撞的。
        然后看Search for a shortest path。这里设计两个问题：1.怎样定义距离长短；2.怎样找到最短路径。对于第一个问题，作者采用了一种尺度$\rho_{path}:C \times C \rightarrow [0,+\infty)$。$\rho_{path}$的计算方法和前面的$\rho_{coll}$相似，也是一种加权距离；不同点在于权值取为$\frac{1}{v_{i}},i=1, \cdots ,d$，$v_{i}$是关节i的最大角速度。之所以这么定义，是因为此论文主要针对机械臂问题，C-Space定义为$I_{1} \times \cdots \times I_{d}$，其中$I_{i}$表示第i个关节的活动范围。权值为角速度的倒数，说明时间越大，权值越大。因此，它的距离长短就被表示为时间长短——走完某条路径花费时间越短，$\rho_{path}$就越短。对于第二个问题，作者采用了$A^{*}$算法。众所周知，该算法找到的路径就是最短路径。如果$A^{*}$ 找到路径了，就对其进行碰撞检测；如果没找到，或者转到Node enhancement，或者返回failure，这取决于规定的时间有没有用完。
        接着看Check path for collision。终于到了碰撞检测的时候。先检测点，后检测边，因为一旦点有碰撞，就会将点删除，同时也会删除与该点相关连的边，这样使算法执行更快。检测顺序是从路径的两头向中间检测，点和边都是如此（具体原因我还没有搞清楚）。检测边时采用将其离散化的方法，先离散化到一个粗一些的分辨率，若检测无碰撞则再进行细化。这样的好处是可以避免很多不必要的碰撞检测。如果边有碰撞，则删除之，然后重新查找最短路径。为了提高规划效率，算法会记录某点是否已被检测过、边的分辨率已经达到多少，这些信息都是可以复用的。然而，分辨率应该如何确定呢？首先，采样点$q,q^{'}$ 之间边的分辨率肯定和$rho_{coll} left (q,q^{'} right )$正相关（试想，边越长，越有可能发生碰撞，于是一个稍大的分辨率就有可能达到检测目的）；其次，分辨率应该和C-Space的规模反相关（试想，对于同一条边而言，它在规模较大的C-Space中会显得较短，障碍物也会显得更小，因此需要把边划分地比较精细才能准确地检测碰撞，这就是分辨率的相对性）。于是，作者给出分辨率公式：$delta= frac {rho_{coll} left (q,q^{'} right )}{M_{coll}}$。其中，$M_{coll}$是C-Space中一条可能的最长直线路径需要进行的碰撞检测数，显然，如果把C-Space想象成一个d维“矩形”，它的可能最长直线路径就是对角线。如果$q,q^{'}$分别位于对角线的两端，那么分辨率为1；否则，分辨率小于1。
        再看Node enhancement。这涉及到一个问题，即应该把这些增强点放到哪里。论文作者采用了和经典PRM类似的办法，先从图上选择一些待增强点，称作种子（seeds），然后把增强点放在这些种子附近。但是，并不是所有的增强点都被放到了种子附近，而是“对半分”，即如果决定产生$N_{enh}$个增强点，则只把其中的一半放到种子周围，另一半则在C-Space中均匀分布。这一方面是因为我们想要获取更多的关于C-Space的信息，另一方面是因为不想太依赖于种子点的选取。
        下面就看看怎样选择种子点。论文作者的想法是“变废为宝”，即把一些因为有碰撞而被删除的边的中点作为种子，这些边要满足一个条件：至少有一个点位于F中。这样选取种子，可以保证其相对靠近F边界，而F的边界通常是困难区域，需要增强。现在考虑一种情况：某个待增强点被选做种子，然后会有增强点出现在其周围，与之相伴而来的还有一些连接增强点和其邻域点的边，这些边有的无碰撞，有的有碰撞并且被删除。下次选择待增强点时，又将这些被删除的边的中点利用起来，它们的周围又会出现增强点。照此执行下去，无疑会造成点的群聚（cluster）。为了避免这种情况，算法在选择种子点时，只考虑那些最初随机均匀产生的边，后面因为增强而增加又删除的边不予考虑。
        种子点选好后，就要讨论一下增强点应该怎样安排了。这里简单给出论文中所使用的方法，不做深入分析。论文使用了多元正态分布的方法。引入两个参数$alpha in left (0,1 right )$和$lambda > 0$，论文作者展示了他们可以选择一种分布，使得事件$rho_{coll}left (q,eta right )leq lambda R_{neighb}$以概率$1-alpha$发生。为了达到这个目标，他们定义了一个协方差矩阵：$Sigma = frac {lambda^{2}R_{neighb}^{2}}{chi_{d}^{2} left (alpha right )}W^{-1}$ 。$\left (\mathbf{q-\eta} \right )^{\mathbf{T}}\Sigma^{-1}\left (\mathbf{q- \eta} \right )$ 是d维$\chi^{2}$ 分布，则事件$left (mathbf{q-eta} right )^{mathbf{T}}Sigma^{-1}left (mathbf{q- eta} right )leq chi_{d}^{2} left (alpha right )$的概率为$1-\alpha$ 。如下图所示：

        其中，$\eta$是种子，q是增强点，C-Space为2维。如果q的分布遵从$N_{d}\left (\eta,\Sigma \right )$，则q位于置信椭圆（实线）中的概率为$1-\alpha$。虚线椭圆是分布函数的边界。
        至此，Lazy PRM算法介绍完毕。实验部分和总结部分略过。


转载本文请联系原作者获取授权，同时请注明本文来自王彦科学网博客。
链接地址：https://wap.sciencenet.cn/blog-795645-627463.html

上一篇：读书笔记——易扩张C-Space中的路径规划
下一篇：读书笔记——一种在障碍物周围产生采样点的随机地图方法