博文
扩张卷积或空洞卷积
||
空洞卷积(dilated convolution)是针对图像语义分割问题中下采样会降低图像分辨率、丢失信息而提出的一种卷积思路。利用添加空洞扩大感受野,让原本3x3的卷积核,在相同参数量和计算量下拥有5x5(dilated rate =2)或者更大的感受野,从而无需下采样。扩张卷积(dilated convolutions)又名空洞卷积(atrous convolutions),向卷积层引入了一个称为 “扩张率(dilation rate)”的新参数,该参数定义了卷积核处理数据时各值的间距。换句话说,相比原来的标准卷积,扩张卷积(dilated convolution) 多了一个hyper-parameter(超参数)称之为dilation rate(扩张率),指的是kernel各点之前的间隔数量,【正常的convolution 的 dilatation rate为 1】。
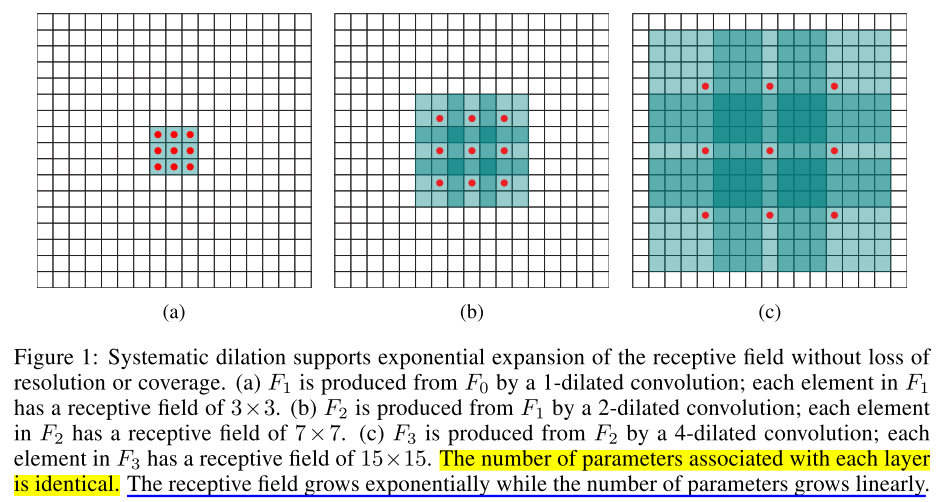
dilated=2时具体的操作,即按照下图在空洞位置填入0之后,然后直接卷积就可以了,如下:


上图是一个扩张率为2的3×3卷积核,感受野与5×5的卷积核相同,而且仅需要9个参数。你可以把它想象成一个5×5的卷积核,每隔一行或一列删除一行或一列。
在相同的计算条件下,空洞卷积提供了更大的感受野。空洞卷积经常用在实时图像分割中。当网络层需要较大的感受野,但计算资源有限而无法提高卷积核数量或大小时,可以考虑空洞卷积。
Dilated Convolution感受野指数级增长
对于标准卷积核情况,比如用3×3卷积核连续卷积2次,在第3层中得到1个Feature点,那么第3层这个Feature点换算回第1层覆盖了多少个Feature点呢?



第1层 ----> 第2层 ----> 第3层
第一层的一个5×5大小的区域经过2次3×3的标准卷积之后,变成了一个点。也就是说从size上来讲,2层3*3卷积转换相当于1层5*5卷积。题外话,从以上图的演化也可以看出,一个5×5的卷积核是可以由2次连续的3×3的卷积代替。
但对于dilated=2,3*3的扩张卷积核呢?


第1层 ----> 第2层 ----> 第3层
可以看到第一层13×13的区域,经过2次3×3的扩张卷积之后,变成了一个点。即从size上来讲,连续2层的3×3空洞卷积转换相当于1层13×13卷积。
意义与问题
最早出现在DeeplLab系列中,作用:可以在不改变特征图尺寸的同时增大感受野,摈弃了pool的做法(丢失信息);
Dilation convolution(扩张卷积)的原理其实也比较简单,就是在kernel各个像素点之间加入0值像素点,变向的增大核的尺寸从而增大感受野。
(1)经过dilation rate放大后,fliter大小上升为:d*(k-1)+1;
(2)扩张卷积的输入和输出特征图的尺寸关系如下:
ps:在s=1,k=3时,令d = p,则输出特征图尺寸不变;扩张卷积可用于图像分割、文本分析、语音识别等领域;
存在的问题:棋盘效应(特征图不是处处可导!)


解决方法:使用锯齿状的卷积核

【参考】
https://www.cnblogs.com/zf-blog/p/12101300.html
https://www.zhihu.com/question/54149221
Multi-Scale Context Aggregation by Dilated Convolutions
点滴分享,福泽你我!Add oil!
https://wap.sciencenet.cn/blog-3428464-1281827.html
上一篇:转置卷积(transposed convolution)或反卷积(deconvolution)
下一篇:深度学习中不同类型卷积的综合介绍--通过可视化直观了解卷积
全部作者的其他最新博文
- • [转载]太阳同步轨道
- • 膳食指南