博文
90周年专栏 | 外加电磁场下周期性体系的第一性原理计算方法
|

外加电磁场下周期性体系的第一性原理计算方法
吕程烨1),陈英炜1)2),谢牧廷1),李雪阳1)2),
于宏宇1)2),钟阳1)2),向红军1)2)3)†
1) 复旦大学物理学系与计算物质科学研究所, 计算物质科学教育部重点实验室, 上海 200433
2) 上海期智研究院, 上海 200030
3) 人工微结构科学与技术协同创新中心, 南京 210093
物理学报, 2023, 72(23): 237102.
doi: 10.7498/aps.72.20231313
《物理学报》创刊90周年专栏特邀文章
摘要 电磁场对物质性质的影响和调控一直是科学研究的核心议题。然而,在计算凝聚态物理领域,由于传统的密度泛函理论并不能轻易推广至含有外加电磁场的情景,且外场往往会破缺周期性体系原本具有的平移对称性,从而使得布洛赫定理失效。因此,利用第一性原理方法计算外场作用下的物质性质并非易事,特别是在外场不能被视为微扰的情况下。在过去的二十年中,许多计算凝聚态物理学者致力于构建和发展适用于有限外场下周期性体系的第一性原理计算方法。本文旨在系统地回顾这些理论方法及其在铁电、压电、铁磁、多铁等领域的应用。本文首先简要介绍现代电极化理论,并阐述基于此理论以及密度泛函理论,构建出两种用于有限电场下计算的方法。然后探讨将外磁场纳入密度泛函理论,并对相关的现有计算手段以及所面临的挑战进行讨论。接着回顾了被广泛用于研究磁性、铁电和多铁体系的第一性原理有效哈密顿量方法,以及该方法在考虑外场时的延伸。最后,介绍了当下备受瞩目的利用机器学习中的神经网络方法构建有效哈密顿量模型的发展成果及在考虑外场下的拓展。
关键词
第一性原理计算,电磁场,有效哈密顿量模型,机器学习
原文链接
01 引 言
“第一性原理计算” 是一种基于量子力学的计算方法,通常以密度泛函理论(DFT)为基础,用于对材料和物质的性质进行数值计算。该方法的优点在于:原则上不需依赖任何经验参数或特定的模型假设,只需要知道构成物质的原子的种类和排布就能从“第一性原理”出发得到计算结果。因此,第一性原理计算方法在物理学、化学、材料科学、地质科学等领域中有着广泛的应用。
DFT最早由Hohenberg和Kohn[1,2]在1964年提出,他们证明了如下两条定理(即HK定理):基态非简并的多体电子系统的性质由基态电子密度唯一决定;且系统能量可视为密度的泛函,当密度取基态密度时,能量取最小值即基态能。然而,这两条定理并没有给出能量泛函的具体形式,所以DFT在此时仍然只是一个形式理论。为使DFT成为一个可实际使用的理论,次年即1965年,Kohn和Sham[3]提出了著名的Kohn-Sham (KS)方法:他们引入了一个虚拟的无相互作用电子系统(即KS系统),该系统的基态电子密度与真实系统相同,因此可以通过求解KS系统来得到真实系统的基态电子密度和基态能量,从而将复杂的多电子问题转化为可解的单电子问题。在这个方法中,每个电子都遵循相同形式的哈密顿量,其中势能分为三项,
VKS(r)=Vext(r)+VH(r)+Vxc(r),分别为外势(包括原子核对电子的库仑吸引势Vn)、电子哈特里(Hartree)势和交换关联势;交换关联势的具体形式未知,计算中需使用合理的交换关联泛函近似;其中Hartree势和交换关联势都依赖于密度,因此对KS体系的求解需使用自洽场方法[3]。由于密度泛函理论在后世的应用几乎都基于KS方法,所以二者又常被合称为KS-DFT。
通过施加电场或磁场来调控物质性质一向是科学研究的焦点,如在铁电学[4]、铁磁学[5]、磁光学[6]、自旋电子学[7]、谷电子学[8]、超导材料[9]、多铁材料[10]、低维材料[11]、巨磁电阻效应[12]、量子霍尔效应[13]、声子霍尔效应[14]等领域中都需要外场的作用。为了理解和预言外场下的物性,亟需发展外场下周期性体系的第一性原理计算方法。然而,HK定理的证明严格依赖于多体哈密顿量的形式和基态的存在性,因此DFT并不能直接应用于外加匀强电磁场的情形,这无疑是一个重大的挑战。传统的解决办法是将外场视为微扰,利用基于线性响应的格林函数方法[15]或密度泛函微扰理论(DFPT)[16,17]进行计算,但这些方法不能适用于有限场(包括强场)的情形。
本文将着重回顾近几十年来关于有限外场下第一性原理计算方法的进展和应用。若无特殊说明,本文公式均选用原子单位制,即ℏ=e=me=1(其中ℏ为约化普朗克常数,e为电子电荷量,me为电子质量),且本文默认采用玻恩-奥本海默近似。
02 有限电场下的DFT计算
在经典电磁理论中,一般用极化强度的变化来描述绝缘体(或称电介质)对外电场的响应。同样地,在后续部分,我们将看到有限电场下的第一性原理计算也直接依赖于对极化强度的计算。尽管外电场产生的外电势不符合无限大晶体的周期性边界条件,但极化强度却可以在原胞中明确定义。因此,在讨论有限电场下的第一性原理计算时,必须首先讨论极化强度的计算。值得注意的是,本文讨论的极化强度以及对外电场响应的计算只适用于绝缘体。对于周期性的金属体系,目前尚无可靠的第一性原理方法。
2.1 现代电极化理论
根据经典理论,当晶体极化时,晶体分子的正负电荷中心会发生偏移,从而形成电偶极,极化强度矢量就是单位体积内的电偶极矩。但以上定义只是宏观层面的,而微观层面的电极化定义和计算直到20世纪90年代才由Resta等[18-22]发展成熟,这一理论后来被称为“现代电极化理论(MTP)”。对于我们关心的无限大晶体,需要寻找的是极化强度的“体”定义,即不依赖于晶体表面的极化性质。一种直观的定义是把极化强度定义为原胞内的平均电偶极矩(其中Ω是原胞体积,ρ(r)为电荷密度),但这势必会依赖于原胞位置和形状的选取,从而导致结果不唯一,如图1所示。况且即使从麦克斯韦方程组出发,∇⋅P(r)=−ρ(r),电荷密度ρ(r)也不能唯一决定极化强度分布P(r),因为P(r)加上任意一个无散场都满足此方程。以上种种说明周期性体系的极化强度不能由电荷密度唯一决定。

图1 两种原子构成的系统的不同原胞选择[21],两原子电荷分别为Z1=+e (空心圆)和Z2=+3e (阴影圆) (a),(b)包含了完整的原子,但相对位置不同;(c)原胞由一个完整的+e电荷和4个+3e/4电荷组成
MTP的高明之处在于:它并不直接定义电极化强度本身,而是定义极化强度在晶体绝热演化下初末态之间的变化量[18]。事实上实验学家测量的也正是极化强度的变化量而非极化强度本身,如铁电材料的自发极化是通过测量电滞回线得到的。极化强度的变化量可以被定义为
其中i和f分别指代初、末态,总极化强度P 可认为是离子极化强度Pion和电子极化强度Pel的和,离子极化强度定义为
其中Zμ和uμ分别为离子μ的电荷数和位矢。
在绝热近似下,对应本征能Enk的电子本征态仍满足布洛赫函数形式,即ψnk(r)=eik⋅runk(r),其中unk(r)=unk(r+R)是布洛赫函数的周期部分,n为能带指标,k取第一布里渊区中的点,R为晶格的正格矢。由一阶绝热微扰论给出
其中对n求和即对所有共M条占据带求和,f 是自旋简并度,负号来自于电子带负电。由此可以给出与演化路径无关的极化强度:
其中An(k)=i⟨unk|∂kunk⟩就是k空间上的Berry联络。也常将(3)式写成Berry相位的形式:
其中ai是原胞基矢,
是沿倒格矢基矢bi方向的Berry相位,是第一布里渊区的体积。极化强度正比于Berry相位的事实也暗示了其应当是多值的,因为Berry相位在相差2π的意义上是规范不变的,即
,m为任意整数。所以并不能直接比较(2)式和(3)式给出的极化强度的大小,但是两个状态的极化差可以通过构造一个绝热演化路径唯一确定。此外(3)式还有一个更具物理直观的诠释:定义Wannier中心
其中Wannier函数
则(3)式可改写为,即极化强度正比于各个占据带的Wannier中心的简单相加,Wannier中心在此处起到了如同经典图像里“负电荷中心”的作用。由于波函数在不同k点可以有任意相位,因此我们可以有无穷多种Wannier函数的选取方法,但在实际计算中一般需要选取最局域化的Wannier函数[23,24]。
需要指出,前面讨论的MTP是一个单电子理论,真实体系的极化强度应由多体理论给出[25,26]。Resta等[26,27]通过巧妙构造与周期性边界条件适配的多体位置算符给出了多体极化强度的正确定义,其在多体波函数取Slater行列式时退化到单体的MTP。
2.2 固定电场方法和电热焓
现在需要研究电子在有限大外电场E 中的性质。考虑KS-DFT框架,晶体中电子的哈密顿量写作[28]:
其中是不含电场的KS哈密顿量,其势场VKS(r)=VKS(r+R)为周期势场。但外电势能项E ⋅r 并不是周期的,这导致了布洛赫定理的失效;更严重的是,外电势是无界的,这使得
没有严格意义上的基态,因为总可以使电子逆着电场线运动来达到更低的能量。从能带论的图像来说,外电场使得能带发生了“倾斜”,从而使原来在一处导带的电子可以跃迁至另一处的价带,这种带间跃迁被称为Zener隧穿[29–32]。不过在很多我们关心的时间尺度内,Zener隧穿可以被忽略,理论上也能证明绝缘体在不太强的电场下处于一种极化的、依旧保持周期性的长期共振态[33],而这正是我们感兴趣的状态。为求解该态,Souza等[32–35]于2002年提出了一种基于KS-DFT和MTP的算法,下面进行简要介绍。
当存在外电场时,我们认为体系“基态”仍处于极化的布洛赫态ψnk(r)=eik⋅runk(r),此时体系的总能量可以用电热焓F 来描述,体系“基态”即对应于取电热焓为极小值时的波函数。考虑体系对外电场的响应,电热焓F 可以定义为[36]
其中P=Pion+Pel是总极化强度,离子极化强度Pion和电子极化强度Pel分别由(2)式和(3)式给出。需要指出的是,ψnk并不是哈密顿量的本征态,但可以被视为对单粒子密度矩阵的表示,且该密度矩阵仍保留有周期性[32]。在对(6)式进行最优化时,可认为外电场E 是一个常量,因而该算法又被称作“固定电场方法”。物理上这对应于给材料施加一个恒定的电压(暂不考虑形变),即将材料两端分别与电源的正负极相连形成闭路。基于电热焓需要取到最小值,数值上可以采用预条件处理的共轭梯度法来求解该最优化问题[35]。
我们有时需要对原子的位置以及原胞的大小进行更新。这里以优化原子位置为例:借助于Hellmann-Feynman定理,可以计算离子受力,该式第1项与传统DFT计算一致,第2项则是外电场对离子的作用力,其中Zμ为μ离子的电荷数。另一种常见的离子受力算法需利用玻恩有效电荷Fμ ≈ Zμ∗⋅E,其中μ原子的玻恩有效电荷张量定义为
,一般通过极化强度关于μ原子沿β方向位移uμ,β的有限差分得到。基于受力,可以通过共轭梯度法或其他优化方法来优化原子位置,使总能最小。值得一提的是,我们可以通过牺牲一定精度来提高效率。Fu和Bellaiche[36]直接利用零场下的玻恩有效电荷来计算加电场后的原子受力,以结构优化,而舍弃了对电子波函数的优化,也可以计算出体系的由晶格主导的压电和介电响应系数,且与实验结果符合得较好;同时,利用这种方法还可以计算体系的电滞回线[37,38];此外,利用零场玻恩有效电荷来近似有限场下玻恩有效电荷,在后文将要介绍的有效哈密顿量方法中也十分普遍。
但该算法也存在一系列问题。如果k 空间取点过密,则F将不存在极小值,从而导致算法失效;而在一般的DFT计算中,k 空间取点越密意味着计算越精确。这个缺陷的背后是两种特征长度的比较:其一是Zener隧穿距离Lt=Egap/|E|,其中Egap为能隙大小;其二是Lp=2π/|Δk|,其中Δk为k点采样间距,该特征长度可以被视为施加周期性边界条件的长度。为能正确求解“基态”波函数,我们需要求Lp<Lt,即在所给范围内不发生隧穿,这就在电场固定时给出了k 点采样的上限,Ni < Egap / |E ⋅ai|。此外,以共轭梯度法求解(6)式的最优化问题时,可以发现某一个k点处的波函数的梯度不仅包含其自身,还包含了临近k 点的波函数信息;而通常的无外场的DFT计算往往对不同k 点进行并行处理,以加快计算效率。但对于固定电场方法,由于不同k 点波函数信息的强烈耦合,一般不支持并行处理,这就使得固定电场方法计算速度较慢。目前一些第一性原理软件包实现了固定电场方法的计算,比如Vienna Ab initio Simulation Package (VASP)[39]、Quantum Espresso (QE)[40]、ABINIT[41]等。
利用固定电场方法,可以对体系的介电性、压电性、多铁性等许多相关的物理量进行计算模拟。比如,玻恩有效电荷也可以通过改变电场大小用对受力的有限差分来计算。固定电场方法结合有限差分还可以计算极化率
,以及介电常数εαβ = δαβ+χαβ,其中ε0是真空介电常数。如果在计算中使离子固定不动,将得到电子贡献ε∞;如果同时允许离子和电子的弛豫,则将得到静态介电常数εstatic。同样可以将该方法推广至二阶极化率
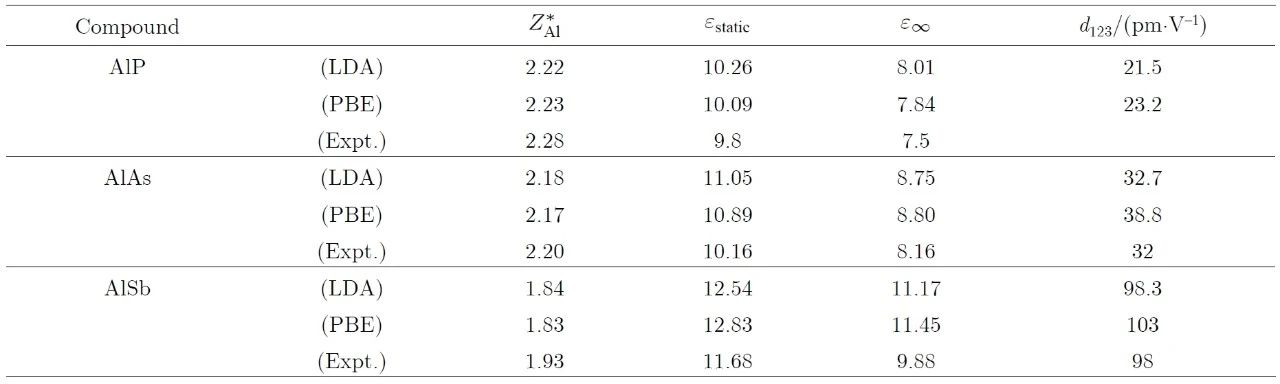
,计算中应固定离子位置。利用不同赝势方法对一些实际体系的介电性的计算结果可见表1,与实验符合得较好[42]。当然,这些零场下的介电性相关的物理量,也可以通过DFPT进行计算[43]。
表1 用固定电场方法计算的一些III-V半导体介电性质与实验的比较[42],其中玻恩有效电荷张量在材料对称性下退化为标量,且d123定义为,LDA和PBE是计算时使用的交换关联泛函近似
压电效应是指当体系施加电场后,会产生原胞的形变。这一效应具有广泛场景,比如压电滤波器、加速器和压力传感器等。可以用压电张量来描述压电效应,其可定义为应力张量对场强的导数,其中
为应力张量,η为应变张量,Vi =E ⋅ai 为电压。但当考虑体系存在形变时,即ai →(1+η)ai时,固定电压Vi 和固定电场E 不再等同,见图2。由于实验上一般是在材料两侧施加固定电压,因此需要基于固定电压法来进行计算模拟。此时电场强度会与应变张量耦合,可以定义约化电场强度E′=E(1+η)和约化极化强度P′=(1+η)−1P 使之解耦[25,26],这样定义的电场强度才是考虑形变时的电热焓的自然变量:
其中Ω(η)是形变后的原胞体积。通常把基于固定电压得到的压电张量称为恰当的(proper)压电张量,而基于固定电场得到的为不恰当的(improper)压电张量,Vanderbilt[44]曾推导过两者之间的转换关系,得到。已经有许多工作运用上述方法,来计算模拟不同体系的压电系数[32,45]。注意到,压电系数还可以表述为
,故也可以通过DFPT进行计算[43]。
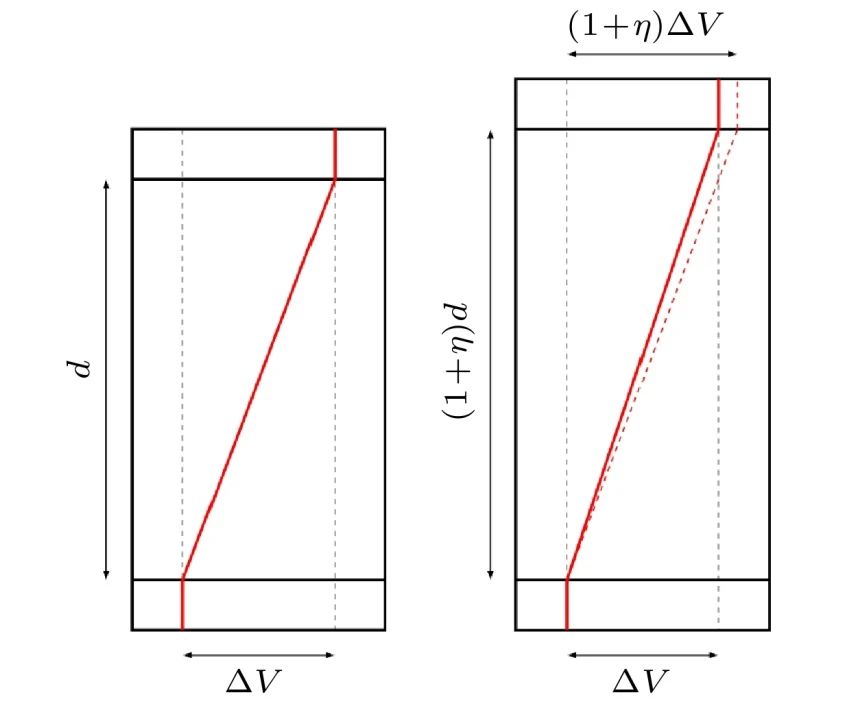
图2 固定电压法和固定电场法的差异[45]。当材料发生应变η 时,如果保持电压ΔV 不变,电场从E =ΔV/d变化为E=ΔV/[(1+η)d];如果保持电场E不变,电压从ΔV变为(1+η)ΔV
固定电场方法同样可以用来研究材料的多铁性。所谓“多铁性”,是指一种材料同时具备铁电和铁磁的性质,该类材料被视为新型多功能磁电器件和高性能信息存储与处理器件的理想候选材料[46]。在多铁性物质的研究中,主要关注如何通过电场调控磁性和通过磁场调控铁电性,所以通常用磁电张量来描述体系的多铁性。借助固定电场方法,可以利用有限差分来计算磁电张量。例如,Malashevich等[47]成功利用了固定电场方法计算了多铁材料Cr2O3中磁矩关于电场的线性响应,从而得到了磁电张量。
最后需要强调的是,尽管该方法计算得出的结果与实验符合良好,但基于一般KS-DFT的方法在原则上并不能给出真实的极化强度,这点最早由Gonze等[48]注意到。该论断的最直接证据是KS-DFT本就不能给出真实的多体波函数,而只能给出正确的基态密度,但我们知道光凭电荷密度是无法确定极化强度的[49]。而根据Gonze等[48]提出的“密度-极化泛函理论”,倘若想同时确定密度和极化强度,则必须引入有效电场E KS,但它并不等于真实的外电场E,二者的差值E KS−E 被定义为“交换关联电场”。
2.3 固定电位移方法和内能泛函
在实验研究中,除了将材料接入闭路即对应固定电场方法外,还可以让其处于开路,这可以通过使测量电路的电阻远大于材料样品的电阻近似实现。在这种状态下,材料两端的自由电荷不会发生转移,从而使得电位移矢量保持恒定。基于这种考虑,Stengel等[50]提出了“固定电位移方法”,其核心是最小化如下泛函(取高斯单位制):
该泛函事实上就是外加电场时原胞的内能。Hong和Vanderbilt[51]以PbTiO3为例,测试了电场随电位移矢量的变化,电位移矢量随极化强度的变化以及极化强度随电场的变化,如图3所示,可见电位移矢量与极化强度之间是一一映射的。
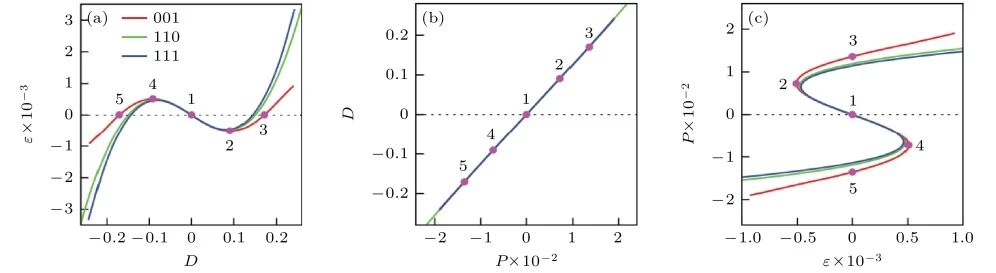
图3 施加场的方向约束在[001],[110]或[111]方向时,PbTiO3中形式为ε(D)(ε为外电场) (a)、D(P) (b)和P(ε) (c) 的电状态方程[51],采取原子单位制
考虑原胞形变时,应保持材料每个面上的自由电荷不变,即电位移矢量的通量不变,此时可定义约化电位移参数不随原胞形变而变化。可以类似地计算得到开路边界条件下的应力张量
。同样可以用固定电位移方法计算开路边界条件下的介电张量
,其中
是电容矩阵的逆,这可以通过有限差分法得到。Jiang等[52]利用固定电位移方法计算了一些铁电体的压电系数。基于开路边界条件,这一方法也适用于计算模拟铁电电容器[50]、超晶格体系[53-55]以及金属-氧化物界面[56-58]。基于固定电位移方法,还可以计算饶曲电张量
,其中
是应变梯度张量[59]。固定电位移方法目前已在ABINIT中得到实现。
除固定电场法和固定电位移法之外,还有固定电极化法[60]。但该方法在物理上对应固定极化电荷,实验上难以实现,所以应用较少。
03 有限磁场下的DFT计算
与电场类似,物质系统对外部磁场的响应通常以磁化强度来描述,磁化强度即单位体积内的磁偶极矩大小。在量子理论中,磁化可根据其来源分为两种:轨道磁化和自旋磁化,它们分别源自磁场与电子的轨道自由度和自旋自由度的耦合。因此,通常将与这两个自由度相耦合的磁场分别称为“轨道磁场”和“Zeeman磁场”。值得注意的是,由于晶体场劈裂的作用,轨道磁矩通常很小,所以磁性材料的磁性几乎全部来自于自旋磁矩;另一方面,轨道自由度对自旋磁矩的贡献一般来自于自旋轨道耦合(SOC)作用,而这一作用往往很小。基于上述两个原因,大部分研究在考虑磁场对材料的影响时,通常会忽略轨道磁场而只考虑Zeeman磁场。
然而,与电场不同的是,无论是Zeeman磁场还是轨道磁场下的体系依然存在基态,这使得对磁场的处理方式至少在原则上是更严格的。尽管如此,当前外场下的第一性原理计算工作仍主要集中于外加电场的情形,对外加磁场的关注较少。鉴于磁场分别与两个不同的自由度耦合,本节接下来将分开讨论Zeeman场和轨道场的影响。除非特别指出,本节的讨论都将忽略SOC作用。
3.1 Zeeman磁场和自旋-密度泛函理论
Zeeman磁场得名于Zeeman效应,即原子光谱在外磁场下劈裂的现象,其物理机制是磁场与原子角动量耦合进而打破了原先的能级简并。而在晶体中磁场主要与自旋角动量耦合,使得自旋向上和自旋向下的电子不再等价,进而导致能带的劈裂。严格考虑自旋的密度泛函理论被称为自旋-密度泛函理论(SDFT),在20世纪70年代由Barth和Hedin [61,62]提出。由于实际体系都具有自旋,在使用中往往不区分DFT和SDFT。
在SDFT中,电子本征态需写成二分量的旋量波函数的形式,其中T表示转置。电子哈密顿量同样需写成2×2的算符矩阵
,其中μB为玻尔磁子,σ =(σx ,σy ,σz)为泡利矩阵矢量,下标σ为自旋指标,取值为自旋向上↑或自旋向下↓(默认自旋量子化轴为z轴),B 为外磁场。显然Zeeman项仅与自旋自由度相关而与空间自由度无关,所以Zeeman场并不改变体系原有的平移对称性,这也说明了我们仍把本征态ψnk 写成布洛赫函数形式的合理性。此时的能量可以视为2×2自旋-密度矩阵的泛函(当密度矩阵取基态密度矩阵时,能量泛函取最小值即基态能):
其中EKS是零场下的能量,−mtot⋅B是Zeeman项,总自旋磁矩是自旋磁矩分布在原胞内的积分,自旋-密度矩阵定义为
,fnk为旋量波函数的占据数,做自洽计算时应使得整个密度矩阵收敛。由自旋-密度矩阵可以给出电子密度
和自旋磁矩分布
。很显然Zeeman项的作用仅仅是使势能矩阵发生了偏移:
所以Zeeman项可以被自然地吸收进势能项,对(9)式的自洽计算方法与零场时完全一致。
准确地来说,以上介绍的是非共线版本的SDFT[63-67]。共线版本的SDFT假设电子自旋仅能朝上或朝下[61,62,68,69],从而哈密顿量和自旋-密度矩阵的非对角元消失,自旋磁矩分布也简化为。对于实验上测得基态为共线态的体系,可以直接利用共线SDFT进行计算,从而避免非共线SDFT带来的大量计算消耗。历史上共线SDFT的发展也早于非共线SDFT。
施加Zeeman场的方法当前主要用于对多铁材料的磁电张量的计算。Bousquet等[70]采用(9)式第一性地研究了磁电张量(此处定义的磁电张量与前文相差一个磁导率μ,即B =μH,且他们的工作中考虑了SOC和朗德g因子),指出电子贡献的量级可以与晶格贡献相比,因而不能被简单忽略。他们计算了不同大小磁场下 Cr2O3电子极化的变化量(如图4所示),从而计算得到体系的磁电张量。在另一个工作中,Bousquet和Spaldin[71]用同样的方法计算了施以应力下CaMnO3磁电张量电子贡献的非对角元
,发现其呈现出高度的非线性,这也与群论分析对一阶响应给出的限制
=0一致。但需要注意的是,通过外加磁场的方式计算磁电张量在数值上是比较困难的:由于磁场诱导的原子受力很小,往往需要设置一个精度很高的收敛条件,如文献[72]中设置的受力收敛条件是 < 5 μeV/Å。外加Zeeman场的方法目前在ABINIT中已得到实现[41]。
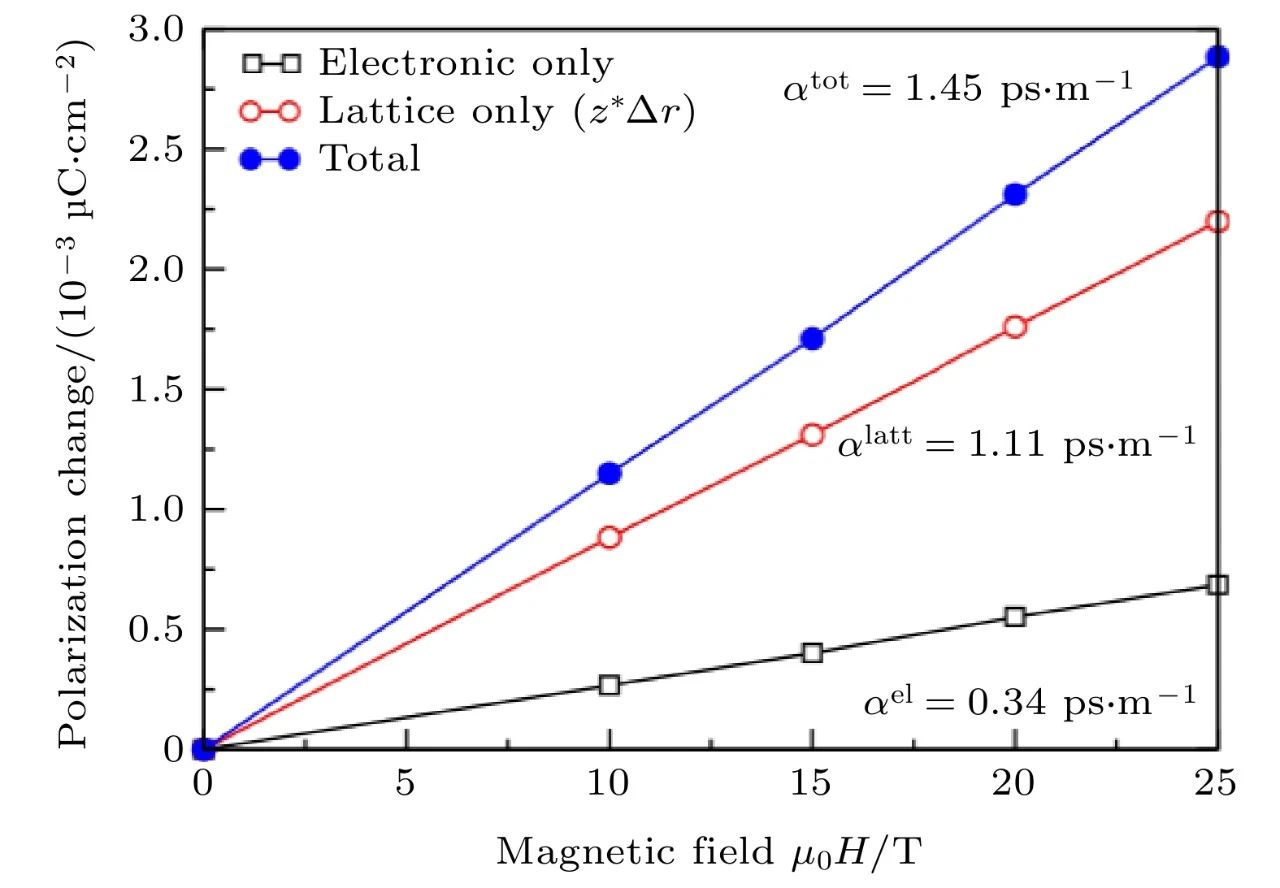
图4 Cr2O3的横向响应贡献[70]。固定离子响应α(el)(空心方块)的贡献约为总响应的四分之一(实心方块);响应的剩余部分(空心圆)来自于外场下的结构畸变,利用波恩有效电荷计算得到
3.2 轨道磁场的密度泛函理论
不同于Zeeman场直接与自旋耦合,轨道场是以磁矢势A的形式与正则动量p耦合,此时电子的动能部分为,其中磁矢势的旋度即为磁场,即∇×A=B。这一改变的影响是显著的:不同于DFT可以简单推广至SDFT,严格考虑磁矢势需对DFT做较大的修改;同时学界对含磁矢势的DFT的关注和发展较少,甚至可以说迄今仍处于起步阶段。本节将简要介绍两种严格考虑磁矢势的类密度泛函理论——电流-密度泛函理论(CDFT)[73-77]和磁场-密度泛函理论(BDFT)[78,79]。在过去十年里,这两种理论在小分子层面已经得到了一定的发展和应用[80-84]。除此之外也有一些含磁矢势的形式理论,感兴趣的读者可以参看文献[85]。
CDFT由Vignale和Rasolt[73]在20世纪80年代提出,其最大特点是同时以顺磁电流密度jp(r)和电子密度n(r)作为基本变量[86],能量泛函在jp和n为基态顺磁电流密度和基态密度时取最小值,此时对应基态能。CDFT的KS方法同样要进行修改,应保证KS系统给出与真实系统相同的基态顺磁电流密度和基态密度。KS-CDFT的能量泛函由下式给出:
其中ϕi 是KS轨道,是通常的不含磁矢势的无相互作用动能,
是无相互作用的顺磁电流密度,EH是通常的Hartree能,
是交换关联能,但此时依赖于密度和顺磁电流密度,Un(r):=Vn(r)+12A(r)2是偏移的原子核势。(11)式对应的KS哈密顿量为
其中AKS(r)=A(r)+Axc(r)和 分别是KS电子感受到的有效磁矢势和有效势,
和
分别是交换关联磁矢势和交换关联势,自洽计算时应使得n和jp均收敛。注意到KS系统的有效磁矢势一般不等于真实系统的磁矢势,这与前文提到的“密度-极化泛函理论”的情况相似,为了使KS系统能给出基态密度以外的物理量,必须引入额外的交换关联势场。
严格来说,以上介绍的是顺磁电流-密度泛函理论,而顺磁电流密度并不是规范不变的,所以历史上也有人试图以规范不变的总电流密度j(r)=jp(r)+n(r)A(r)和电子密度n(r)为基本变量建立“全电流-密度泛函理论”[87,88],但这一理论在数学上存在诸多争议[76,89-91]。
BDFT由Grayce和Harris[78]在20世纪90年代提出,但该理论的后续发展极少。与CDFT不同,BDFT仅以电子密度n(r)作为基本变量,这样做的代价是舍弃了通用密度泛函的构造,如Grayce和Harris[78]所言,“一个磁场对应一个密度泛函理论”。但这个代价对KS方法的影响可能并不大,我们仍然可以把磁场的影响标记在交换关联能Exc[n;B]里。KS-BDFT给出的能量和哈密顿量分别为
其中动能为,交换关联势为
,可见BDFT不需要引入额外的交换关联势场。BDFT与CDFT之间可通过“four-way correspondence”严格联系起来[79];如果忽略交换关联项中的电流或磁场贡献,BDFT和CDFT退化为相同的理论。
以现有水平尚无法判断CDFT和BDFT的优劣,但可以肯定的是:这两个理论的实际应用依赖于合适的磁场下交换关联泛函近似——而这正是目前所缺失的。不过有研究指出meta-GGA或许具有不错的前景[82]。
3.3 现代轨道磁化理论
在3.2节可以看到,轨道磁场下的体系严格具有基态,所以有限轨道场下的第一性计算方法原则上并不需要引入轨道磁化Morb的概念。但考虑到其在核磁共振(NMR)[92]、电子顺磁共振(EPR)[93]、量子自旋霍尔效应(QSH)[94]、轨道磁电耦合[95-98]等领域具有重要意义,本节将简略介绍轨道磁化的理论计算。
轨道磁化的量子力学定义由21世纪建立的“现代轨道磁化理论”给出[99-106]:
其中c为光速,μ为化学势,fnk为占据数。可以发现该理论与现代电极化理论有许多共通之处,但与电极化不同的是:轨道磁化是单值的,其依赖于Berry曲率和哈密顿量;且现代轨道磁化理论适用于有限温和金属情形。对于零温且陈数为零的系统,轨道磁化可以写为更简洁的形式[104]:
对于轨道磁化本身(作为零场性质)的第一性原理计算工作可见文献[93,107],采用赝势法计算轨道磁化时应考虑赝势的磁平移对称性(该对称性将在下文介绍),这种方法被称为“含规范的投影缀加波法 (GIPAW)”[108,109]。
不同于前文所述的处理有限电场或Zeeman场的方法,尚未有在能量泛函中直接添加−Morb⋅B 项来做外磁场下第一性原理计算的工作,这可能是基于对轨道磁矩贡献很小的预设。然而,必须强调的是,在某些特定材料中,轨道磁矩的贡献可能与自旋磁矩相当,甚至有可能占据主导地位[110,111]。
3.4 含磁矢势的周期性体系计算
本节介绍的含磁矢势的周期性体系计算方法来自于Cai等[112,113]的工作,据知,这是目前唯一涉及有限轨道磁场第一性原理计算的工作。引入磁矢势的主要困难依然在于它破缺了平移对称性,从而导致布洛赫定理失效,所以不能方便地选用平面波基矢进行计算。但幸运的是匀强磁场仍保留有一定的对称性,能给出所谓的“磁布洛赫定理”,该方法正是利用了此性质。
我们考虑电子哈密顿量,其中B =∇×A为匀强磁场,V(r)=V(r+R)是一般的周期势。设磁场B 沿a3方向,当其满足磁通量子化条件B ⋅(a1×a2)=2πn0 (n0为正整数)时,哈密顿量的本征态满足磁布洛赫定理:ψnk(r)=eik⋅runk(r),其中
不再满足原胞的周期性边界条件,我们称其为磁周期性边界条件(MPBC)[112]。该定理说明波函数在磁场下的平移会带来一个依赖于规范的相位,这是磁平移对称性的体现[114,115]。同时可注意到,密度即波函数的模方仍然是周期的,与零场情况相同。
为方便起见,本段的讨论仅限于n0=1,Γ点和正交晶胞的情形,此时ψnk(r)=unk(r),取,磁矢势取朗道规范
,并略去本征态的下标。更一般的讨论见文献[113]。在这种选取下,ψ(r)在z方向是周期的,并与x,y无关,可以利用传统的平面波展开处理,故略去此分量。剩余哈密顿量可拆为三部分:
其中和
分别为x和y方向的动能;ψ(r)在y方向上也是周期的但依赖于x,对其进行沿y方向的傅里叶级数展开,其系数满足:
其中Gy=2π/b,Ky=nyGy是y方向的傅里叶指数,称(x, Ky)所在的空间为“介空间”。注意到(18)式事实上给出了螺旋线的拓扑(如图5所示),因而可以定义“弧长参数” :=x +aKy /Gy,将表达式由二维降至一维,
f():=f(x,Ky)=f(x−a,Ky+Gy)。再对f(
)进行傅里叶变换即可得到倒空间函数
(注意该倒空间是介空间的“倒”空间)。这样做的好处是
和
分别在倒空间和介空间对角(如同平面波基矢下动能项在倒空间对角):
,所以
和
应当分别在倒空间和介空间中计算[112]。势能依然由实空间直接相乘得到。
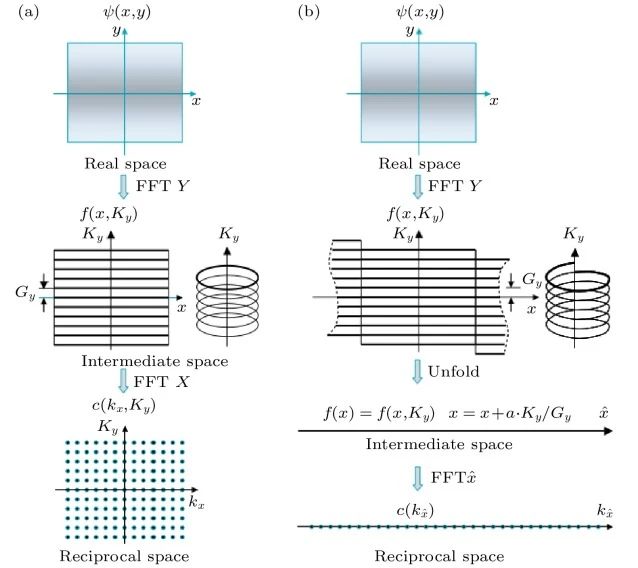
图 5 实空间波函数ψ(x,y)通过两次傅里叶变换到倒空间函数c [112] (a)当B=0时,f(x,Ky)可被视为一系列一维周期函数或圆环;(b)当B=2π/(ab)时,MPBC使其变为一条长螺旋线。由此介空间和倒空间内的波函数可等效为一维函数
Cai等[112,113]利用这种方法计算了磁场下的朗道能级、量子阱中的单电子和双电子能级、氢原子和氢分子能级以及致密氘流体的电子结构。对于致密氘流体,他们发现:在施加强磁场前后,最高占据分子轨道(HOMO)和最低未占据分子轨道(LOMO)变化显著,然而总电荷密度并未发生明显改变,如图6所示。

图6 致密氘流体在零场和强场下的电子结构[112] (a)总电荷密度在B从0升到104 T时基本保持一致;(b) B = 0 (蓝色)和 B = 104 T (红色)时HOMO态在不同原子上的电荷密度分布
04 处理外场的第一性原理有效哈密顿量方法
当代的第一性原理计算软件已经发展得较为成熟,用户通常只需要输入少许参数即可自动化完成计算并输出最终结果,如总能量、极化强度、磁矩等,且结果通常被认为是精确可靠的。但第一性原理在高精度的同时也对算力有较高的要求。受限于计算量,第一性方法往往难以便捷地处理大尺度体系,从而限制了对体系部分动力学和热力学性质的研究;此外,这种自动化计算的流程近乎于“黑箱”,在未经进一步分析的情况下其计算结果并不能带来明确的物理图像。有效哈密顿量方法是为了平衡精度和计算量而诞生的,其旨在使用有限数量的主要自由度来描述原子哈密顿量或其势能部分(通常称为“势能面”),具体参数则根据DFT计算结果来确定。从统计物理的角度来说,有效哈密顿量方法是通过积掉配分函数中的高能或无关的自由度,从而得到了描述低能物理的有效模型。由于其相对较高的精度与相对较低的计算量,有效哈密顿量方法能处理比DFT更大尺度的体系,从而更便利地研究体系的相变过程、热力学性质等,因此在磁性、铁电、多铁等领域得到了广泛的应用[116]。
4.1 磁性体系的有效哈密顿量方法
由于材料磁性几乎都由自旋磁矩引起,构造磁性有效哈密顿量时一般仅考虑自旋自由度,所以也称之为“有效自旋哈密顿量”模型。同时为简化讨论与计算,我们常将原子的局域磁矩和自旋视为定长的经典欧氏矢量而非量子力学算符,即采用了“刚性自旋旋转近似”,这在自旋较大时是合理的,对该近似的进一步讨论见引文[117]。一旦得到了磁性有效哈密顿量,便可以轻易计算出磁构型对应的能量,并借助蒙特卡罗(MC)模拟[118]或者利用Landau-Lifshitz-Gilbert(LLG)方程进行自旋动力学模拟[119-122]来确定磁基态,这两种方法都适用于有限温度的场景。若更进一步地考虑原子位移自由度,有效自旋模型也可以用来做自旋-晶格动力学模拟[123,124]。
有效自旋模型的精度依赖于第一性原理计算的精度,我们将首先介绍磁性体系第一性原理计算中常使用的两种方法:“DFT+U ”方法和约束磁矩方法。由于传统的交换关联近似很难描述磁性体系中局域性较高的d电子和f电子,所以我们常使用所谓“DFT+U ”的方法来补偿局域电子的强关联效应,其中U参数源自Hubbard模型中的在位能,具体计算中需要根据经验或实验值选取[125-127]。此外我们往往需要第一性原理计算能给出不同的磁构型,比如我们希望能计算一个体系所有可能的不同铁磁、反铁磁态。虽然原则上KS-DFT可以给出指定对称性(如指定总自旋量子数)下的最低能态[62],但在实际中通常是利用约束总磁矩或约束局域磁矩的方法来得到想要的磁构型,具体做法是运用拉格朗日乘子法在能量泛函中添加相应的惩罚项[65,128,129]或通过施加局域磁场来约束局域磁矩大小或方向[130,131];其中局域磁矩通常被定义为总磁矩分布在原子附近的积分,ΩI 是以I 原子为球心的截断球,其事实上假设了原子磁矩总局域在原子附近,这对于绝大多数体系来说都是良好的近似。
无外磁场时多体哈密顿量具有时间反演对称性(无论是否考虑SOC),有效自旋哈密顿量Hspin也应具有这个性质,即要求有效哈密顿量在自旋全体反向时保持不变,所以模型中应当仅含有自旋的偶数次项。对于大多数体系,我们只需要考虑二阶相互作用项即可,其表达式为[116,132]
其中i,j 是原子指标,Si 对应于第一性原理计算给出的原子局域磁矩或自旋(假设原子磁矩总与原子自旋共线),和
均为3×3的实矩阵,分别称为单离子各向异性(SIA)矩阵和J矩阵,它们通常依赖于原子的相对位置。不失一般性地,我们可把SIA矩阵
选为对称无迹阵。J 矩阵可分为三部分,
[133,134],其中I 为3×3的单位矩阵,
为各向同性的海森伯交换相互作用参数,
为对称无迹的各向异性交换相互作用(包括Kitaev相互作用)矩阵[135],
为反对称的Dzyaloshinskii-Moriya (DM)相互作用矩阵[136-138]。DM项
也常写成Dij⋅(Si×Sj)的形式,其中
是DM相互作用矢量。不同相互作用倾向于使自旋Si指向不同的方向,体系的磁基态构型依赖于各项的互相竞争。通常体系在零场时的总磁矩取向主要取决于SIA项和Kitaev项;当DM相互作用较强时,体系可能形成螺旋态或斯格明子[139-145]。若忽略Kitaev项和DM项,二阶有效自旋模型将退化为经典海森伯模型。高阶项中得到较多关注的是点积形式的四阶项和高阶手性项,它们在某些材料中也具有显著效应[146,147]。
常见的有效自旋模型参数计算方法大致分为两大类:能量映射分析和格林函数方法。前一大类中常用的方法有拟合法和四态法。拟合法[148-151]指将有效自旋模型预测的能量与第一性原理计算结果一一比较,根据最小二乘法确定参数的方法。拟合法原则上可以计算所有类型的相互作用,且可以通过数据分析确定参数的不确定度;但该方法需要预先生成大量磁构型,计算量大。由Xiang等[152,153]提出的四态法则是一种计算量较小的能量映射分析方法。在这种方法中,我们需要假设体系仅包含二阶相互作用,可发现要确定其中任何一个独立的参数(可以是矢量或矩阵的一个独立分量),都只需计算4种指定自旋构型的总能量即可求解(指定自旋构型一般通过约束局域磁矩实现),其余参数的影响都能恰好消掉[132,152,153]。该方法的缺点是受高阶相互作用影响较大,但特定的高阶项仍可以通过巧妙选取自旋构型消除[151]。近年来,为确定复杂体系的有效哈密顿量具体形式及各项参数大小,Li等[154]基于变量筛选(variable selection)算法发展了一种新型的能量映射分析方法——机器学习方法构造有效哈密顿量(MLMCH)方法,其可以高效而准确地在诸多备选相互作用形式中挑选出重要的相互作用项,从而建立简洁准确的有效哈密顿量;相较于后文将要介绍的神经网络方法,MLMCH方法能给出解析的有效哈密顿量形式。该方法的可靠性已在有效自旋模型中得到验证,并集成在PASP (property analysis and simulation package) 当中[132,154,155]。格林函数方法同样应用广泛[156-161],该方法主要利用了磁力定理[162]:对基态的微扰(这里是两个原子自旋的微小旋转)等于固定的基态势能下粒子(这里是电子)能量变化之和。该方法的优势是仅需3次第一性原理计算即可求得所有的二体二阶项参数和双二次项(属于四阶项)参数,且仅需用到晶胞而不需要能量映射分析方法中为减小周期性边界条件影响而使用的较大超胞[163,164];然而,该方法依赖于基组的选择,对于非磁性原子局域磁矩较大的体系难以准确描述,且对于明显偏离参考构型的自旋构型能量有可能预测不准。
若将外磁场B 纳入有效自旋模型,只需要给哈密顿量添上Zeeman项:
其中g为朗德g因子,用于描述轨道磁矩对总磁矩的修正。这一方法在研究磁场对磁性物质的调控方面十分常见。典型的研究如利用其计算磁化强度和居里温度随磁场的变化,在考虑温度时也可以研究磁热效应[165]。此外,磁致相变也通常是研究的重点,如以此法计算发现稀土铁石榴石在补偿温度附近急剧的全体自旋翻转[166]。一类有代表性的研究是用磁场诱导斯格明子态[167-173]:如文献[168]发现随着磁场的增大,低温下的Pd/Fe/Ir(111)体系发生了由螺旋态到斯格明子再到顺磁态的相变;文献[173]则更为细致地研究了CrGe(Se,Te)3 Janus单层在不同温度和磁场下的复杂相图,如图7所示。CrGe(Se,Te)3同时具有很强的DM相互作用、阻挫效应和较强的面外各向异性,这些特性都有助于斯格明子的稳定,因而其被认为是研究斯格明子的理想材料[139,173-175]。
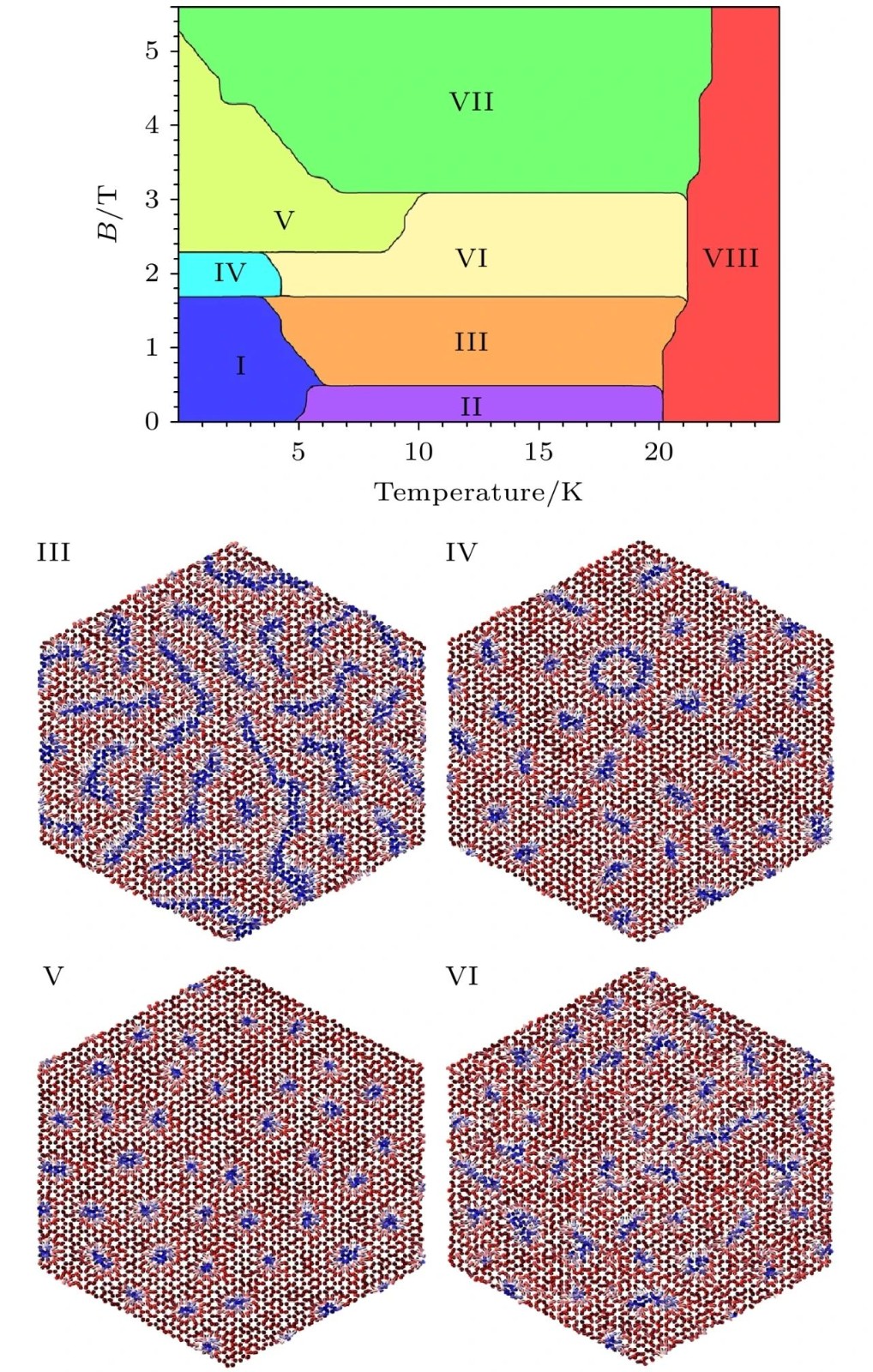
图7 CrGe(Se,Te)3 Janus单层的磁场-温度相图[173]。相边界由热容、磁化率、局域自旋手性决定。这8个相描述为破碎迷宫畴、斯格明子与嵌套斯格明子合相(I)、迷宫畴(II)、破碎迷宫畴与斯格明子混合相(III)、孤立斯格明子与嵌套斯格明子混合相(IV)、孤立斯格明子(V)、杂化斯格明子相(VI,部分斯格明子合并,部分斯格明子保持分离)、饱和铁磁态(VII)、顺磁态(VIII)。如图所示为相III (B =1.8T,T = 4.14K)、相IV (B=1.8T,T = 4.14K)、相V (B =2.4T,T=4.14K) 和相VI (B =2.4T,T = 13.3K) 的代表性自旋结构
4.2 铁电体系的有效哈密顿量方法
一般认为,铁电相变在宏观上遵循朗道的对称性自发破缺理论,材料由无自发极化的顺电态(PE)向有自发极化的铁电态(FE)的转变就是体系从高对称态“破缺”到了低对称态。从具体机制上来看,铁电相变又可分为位移相变和“有序-无序”相变,前者指原子发生位移使晶胞从高对称结构(通常具有中心反演对称性)变为无中心反演对称性的低对称结构并产生了自发极化;后者指晶胞本身存在自发极化,但因晶胞的随机排布宏观上不显极化,宏观上的自发极化来自于晶胞排布由无序转为有序的过程。真实材料的铁电机制可能介于二者之间。Cochran[176]指出,晶体的位移相变是由那些不稳定的声子模式驱动的,这些模式被称为“软模式”,其频率呈虚数[177]。在相变点附近,某些声子之间的非谐性相互作用过强以至于原子事实上偏离了原先的平衡位置,在越过相变点之后声子模式才重新稳定。这些事实表明描述铁电相变(至少是位移相变)的机理仅需要用到软模声子的自由度。
铁电的有效哈密顿量方法由Zhong等[178,179]最早于1994年建立,他们用这种方法成功解释了铁电材料BaTiO3的相变机理,是铁电研究史上的里程碑。铁电有效哈密顿量选取的自由度一般是局域应变η和若干个“局域模式”u,其中局域应变又可以分为均匀应变ηH和非均匀应变ηI,前者表示晶胞的整体形变,后者表示晶胞角落的局部位移、对应于Γ 点附近的声学声子;局域模式指的是原胞内一些原子的集体运动,不同原胞内局域模式的组合可以得到非局域的软模,这种选取方式被称为“局域模式近似”[180-182]。局域模式自由度考虑到了原子的有限位移,所以原则上可以同时描述位移相变和“无序-有序”相变。更严格的局域模式定义需用晶格Wannier函数给出[183],但这一形式应用较少,常见的做法仍是将局域模式写成原子位移叠加的形式。
常见的零场下铁电有效哈密顿量EFE由五项组成[179]:
分别为局域模式自能、长程偶极-偶极相互作用能、短程软模相互作用能、弹性势能和局域模式与应变的相互作用能。对于铁电相变,局域模式往往选为Γ点的光学声子模式。有些用于研究合金的铁电有效模型也考虑了表征同位点原子种类差异的构型自由度σ(σ=±1)[184]和原子体积差异的局域应变自由度ηloc[185]对能量的影响。此外,由于实际体系中也存在由其他软模声子驱动的反铁畸变(AFD)相变和反铁电(AFE)相变,因此许多有效模型也包含了AFD自由度和AFE自由度[186-190],在这里仍将其统称为“铁电有效哈密顿量”模型。
在铁电有效哈密顿量中考虑外电场的效应一般通过引入局域模式的玻恩有效电荷和固定离子的压电张量e实现,即把极化强度写为
。这样给出的外电场下铁电有效模型为[191]
该模型与MC模拟相结合,可以用来计算电斯格明子态[192]、反铁电相变[189]、电热系数(S为熵)[193-196] (如图8所示)等,考虑挠曲电效应时也能计算挠曲电系数[197]。此外,有效哈密顿量中可以比较方便地引入退极化场,这在部分工作中也已经得到体现[198,199]。另一种常见的方法是利用有效哈密顿量做分子动力学模拟(MD),目前利用有限电场下MD方法研究得较多的是铁电相变、电热效应等[200-202]。
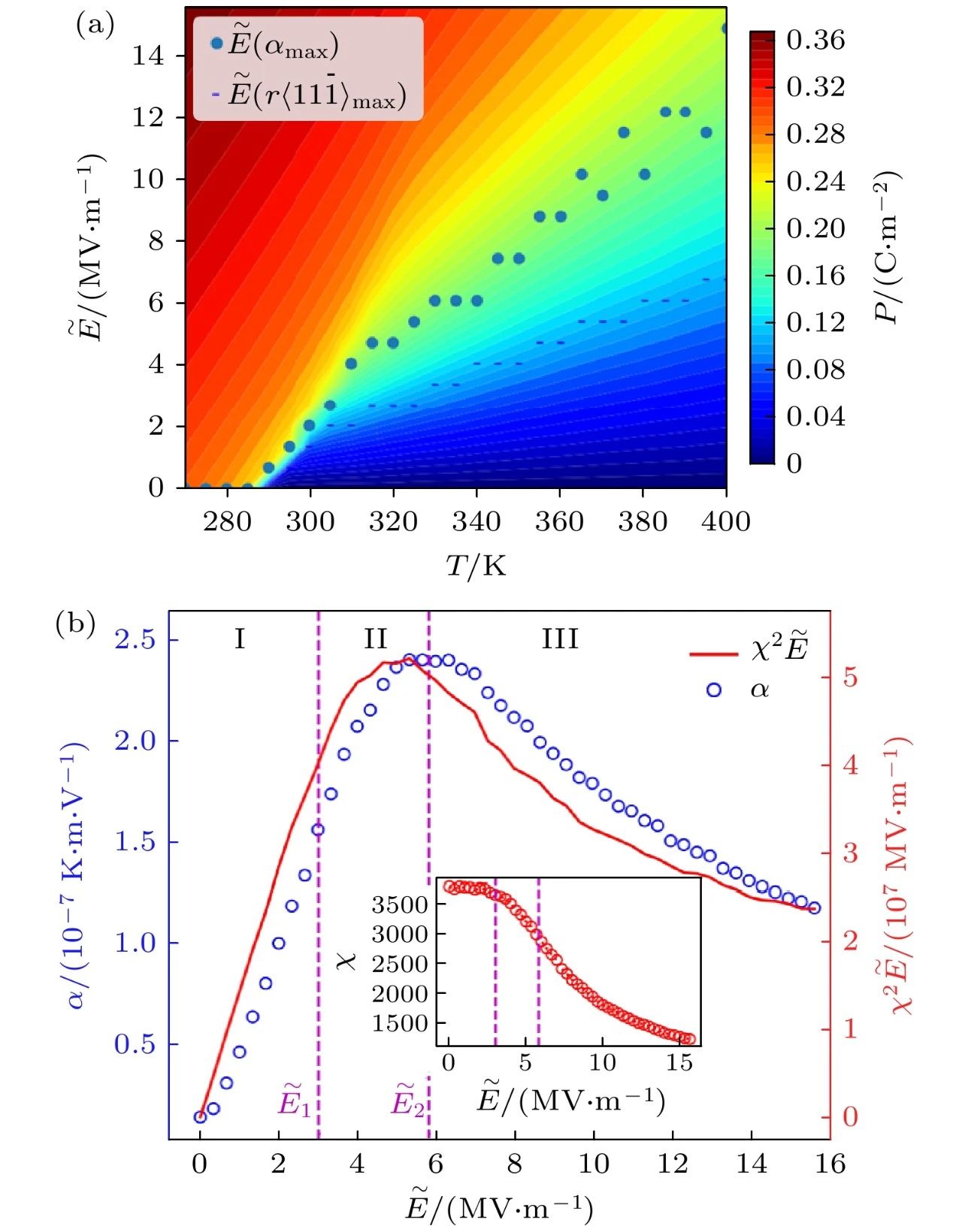
图8 铁电材料PbSc0.5Ta0.5O3 的电热效应[195] (a) 铁电材料PbSc0.5Ta0.5O3的极化强度P(,T)关于沿⟨111⟩方向施加的电场
和温度T的函数;(b) 电热系数α在330 K时随电场E的函数关系。在研究温度下时使α达到极大值的电场[
(αmax)]和固定温度时使得
达到最大值的电场[
(
)]也标记在图(a)中。χ2
也在图(b)中标出以与α做对比。
是大致沿
,
或
方向的局域偶极矩的比例
Vanderbilt的铁电有效模型原先是基于施加周期性边界条件的超胞设计的。Fu和Bellaiche [203]则对此模型进行了扩展,开发出适用于开放边界条件的铁电有效哈密顿量方法。他们使用这种新方法并结合外加电场来研究铁电微纳点的铁电性质,发现在电场驱动下,铁电微纳点可以产生显著的极化效应。Prosandeev等[204]随后把这种方法拓展到非匀强电场的情形,体系对电场的响应由每个局域电偶极单独贡献−pi ⋅Ei,其中pi和Ei为i 位点处的局域电偶极和电场大小,他们利用这种方法计算研究了横向非均匀电场对电环矩(electric toroidal moment)的调控。
4.3 多铁体系的有效哈密顿量方法
多铁材料可分为两类:I型多铁和II型多铁。I型多铁通常是良好的铁电体,并且铁磁和铁电相变的温度可以远高于室温,但此类材料内部的磁性与铁电性的耦合通常很弱。II型多铁是新型的多铁性物质,其铁电性仅存在于磁有序状态中,并且是由特定的磁序引起,因此该种材料的磁电耦合较强。目前主要有两种基于有效哈密顿量研究多铁体系的方法。
其一是基于有效自旋哈密顿量方法。但因为有效自旋模型不显含电场和极化相关的信息,该方法往往需要额外的DFT运算。Sasani等[205]借助海森伯模型研究了GdFeO3的非线性磁致极化现象并给出了与实验符合的结果,他们通过旋转Gd子晶格的磁序将极化强度的变化量表示为G型反铁磁序(是Gd原子和Fe原子的主要磁基态)强度的函数,这一过程中需要固定Gd子晶格的磁序但弛豫原子位置和Fe子晶格的磁矩,并且每一步都需要利用MTP计算极化强度。Xu等[37]将有效自旋模型与固定电场方法结合,提出了以极化强度和DM相互作用为中介、用外加电场可控可逆地调节I型多铁体系的磁性拓扑荷的机制(EPDQ机制),其中有效自旋模型参数需根据电场诱导的体系结构确定。
其二是将有效自旋哈密顿量纳入到铁电模型当中来构建统一的多铁有效模型,即:
此时的有效自旋模型Hspin还包含了自旋与其他自由度的耦合项[206-211]以及长程偶极相互作用项[206]。
考虑多铁材料在外电场下的响应,则此时的极化强度P原则上也应当是({S},{u},{η})的函数:
然而,对于I型多铁材料,由于磁性和铁电性互相较为独立,可以忽略自旋对极化的贡献,极化强度仍写为。但Bhattacharjee等[212]通过MC模拟证实了电场对极化的切换依然能对体系磁序产生重大的影响,这也与EPDQ机制一致。而对于磁电耦合显著的II型多铁,我们必须考虑自旋对极化的影响:例如Xiang等[213-216]通过建立自旋序诱导的统一极化模型P({S},{u},{η}),成功解释了II型多铁性材料的物理机制。II型多铁性材料的原子位移通常不大,所以可以把极化强度近似写为电子贡献和离子-晶格贡献之和P =Pe({S})+Pion,latt({u},{η}),其中电子贡献又可写为
是在位贡献,Pij(Si,Sj)是位间贡献,⟨i,j ⟩表示最近邻。电子贡献与离子贡献的系数都能通过四态法计算得到[215,216]。然而,据知目前尚未有基于统一极化模型建立外电场下的多铁有效模型的工作。
将外磁场引入多铁有效模型的方法与自旋有效模型一致,即仅需考虑(20)式中的Zeeman项即可。Kornev等[206]采用这种方法计算了BiFeO3块体的磁电系数,与实验符合较为良好;Xu等[116,217]基于此模型系统地研究了反自旋-电流相互作用(可视为一种特殊的DM相互作用)对BiFeO3磁结构的影响(如图9所示)。特别地,对于II型多铁性材料,还可以利用统一极化模型研究和自旋磁矩相关的磁电效应。
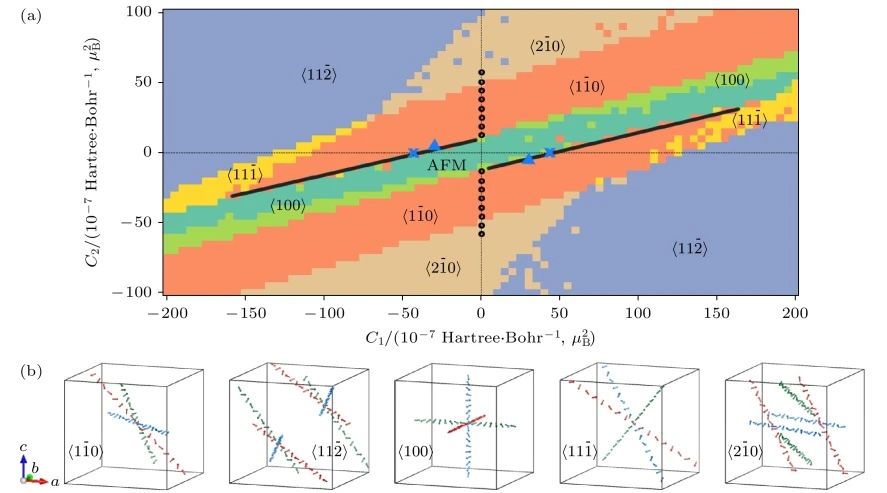
图 9 块体BiFeO3在各种C1和C2值下预测的磁性结构[211],其中C1和C2分别是第一近邻和第二近邻的反自旋-电流相互作用系数 (a) 计算得到的相图与C1和C2的函数关系,蓝色十字标志和黑色圆点分别代表来自前人选取的C1值(此时C2=0)和C2值(此时C1=0),蓝色三角表示通过密度泛函理论计算得到的结果,黑线是磁场大小为18 T时螺旋相向反铁磁相转变的临界相;(b) 图示展示了5种类型的磁螺旋的传播方向,对于每种类型,红色、蓝色和黄色分别代表了不同传播方向的等效磁螺旋
4.4 机器学习势函数方法
近十年来,机器学习(ML)方法和材料建模与计算的融合成为发展最快且最具前景的研究领域。相较于前文讨论的传统方法,机器学习方法在保持高精度的同时显著提升了计算效率,使得原先需要数小时甚至数天的计算在几秒或更短的时间内完成。大部分的材料机器学习模型是基于核的机器学习算法,该算法利用材料的描述符作为输入,基于核脊回归(KRR)和高斯过程回归(GPR) 等方法学习输入描述符与相应材料能量之间的映射函数[218-223],如原子间势场模型DPMD[223]。然而,近年来这些方法逐渐被性能更优秀的图神经网络(GNN)算法取代[224-228]。图神经网络采用连通图来表示材料的几何结构,网络的图学习结构表示可以直接且自然地从输入结构中学习而无需手动构建,因此可以被视为一种端到端学习的自然描述符。本节介绍的机器学习方法特指利用神经网络、尤其是图神经网络学习并构造有效哈密顿量的方法。
据知,最早基于GNN系统性地构造磁性有效哈密顿量的工作为Yu等[229]提出的SpinGNN,该网络全面地考虑了原子位移自由度和磁矩自由度,对于共线和非共线磁矩均能适用。SpinGNN由两套独立的子网络组成:海森伯边图神经网络(HEGNN)和自旋-距离边图神经网络(SEGNN),如图10所示。前者使用GNN中更新的边特征来映射海森伯相互作用系数,支持学习基本的海森伯模型;后者使用原子距离和原子间非共线自旋的点积来初始化网络中的边,可以学习高阶的磁相互作用;两套子网络可以独立或共同运行,对于一般的海森伯型,相互作用占绝对主导的材料,只需使用HEGNN,而对于相互作用形式更为复杂的材料,应当同时使用两套网络,此时体系能量由二者共同给出,Etot=EHEGNN+ESEGNN。经测试,该网络在预测多种材料的磁相互作用能和自旋-晶格动力学模拟方面展现出了优越的性能。
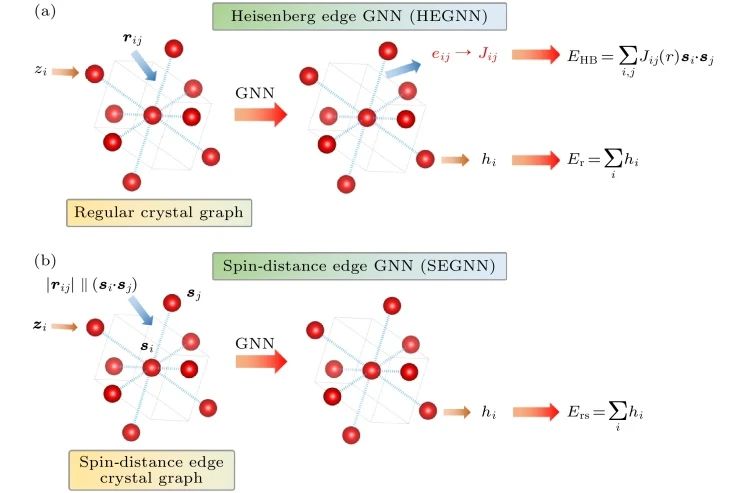
图10 SpinGNN框架[229],SpinGNN包含海森伯边图神经网络(HEGNN)和自旋-距离边图神经网络(SEGNN) (a) HEGNN利用更新后的GNN边特征作为Heisenberg系数,构建Heisenberg型的磁势;(b) SEGNN利用自旋-距离边晶体图,以自旋矢量的点乘和键长初始化边,可以构建一般的高阶磁势,∥表示拼接
最新的图神经网络技术是E(3)-等变图神经网络(ENN)[230-234],它在原有的图神经网络基础上将体系在三维欧氏群E(3) (平移、旋转、反演)作用下的等变性内建在网络之中,从而进一步减少了训练量并提高了预测精度。形式上,一个函数f:X→Y 被称为“G-等变的”指群G的作用与f对易,即:
DY[g]f(x)=f(DX[g]x), ∀g∈G, ∀x∈X,其中DX[⋅]和DY[⋅]是G在线性空间X 和Y上的群表示。在我们考虑的情况下:G 是三维欧氏群E(3),X,Y 分别表示网络的输入和输出信息,f 是E(3)-等变神经网络(ENN)实现的映射,其内部通常根据O(3)群的不可约表示对原子特征进行直和分解,如NeqiuIP[231]和Allegro[232]这两个最近提出的E(3)等变的原子间势场模型。
基于E(3)-ENN构建磁性有效哈密顿量的工作同样来自于Yu等[235],他们成功地将E(3)-ENN扩展至包含时间反演变换的时间反演-E(3)等变神经网络(TENN-e3)。这一扩展是非平凡的,因为原E(3)等变性只考虑到了实空间的对称变换而没有涉及自旋空间和速度空间等,具体差异体现在自旋和速度矢量应在时间反演下变号而实空间里的矢量、张量在时间反演下不变。TENN-e3的输入不仅包含原子间的相对位移rij 和原子电荷数Zi还包含原子自旋Si,内部根据O(3)群的不可约表示和时间反演下的奇偶性对原子特征进行直和分解,因而该方法能适用于考虑或不考虑SOC、共线或非共线的磁性系统,其最终输出任意满足对称性要求的标量、矢量和张量,比如能量和KS-SDFT哈密顿量,因此也能自然推广至外加Zeeman场的情形。
当前使用图神经网络学习外电场下的有效哈密顿量的研究仍处于初级阶段,主流方法仍是基于描述符。Ma等[236]利用DPMD建立了以往模型难以描述的铁电材料HfO2的势场,并采用外电场下的MD方法模拟了铁电反转驱动的氧离子输运。但他们的模型并不能预测玻恩有效电荷和极化强度,模型在外电场下的响应仍需通过传统方法计算。Zhang等[237]利用深度偶极子模型成功预测了原子偶极矩以及绝缘体的介电响应;然而在这种方法中,玻恩有效电荷是通过预测偶极矩间接计算得到的,可能存在精度偏差。此外,该方法需要同时运用两种模型进行电场作用下的MD模拟,因此所需计算成本约为原方法的2倍。
05 总结与展望
本文的目的是介绍有限外电场和外磁场下的DFT计算方法和有效哈密顿量模型方法。首先,回顾了现代电极化理论,以及两种基于此理论构建的有限电场下的DFT算法。然后分别讨论了含Zeeman磁场和轨道磁场的密度泛函理论以及与之相关的现有计算方法。随后,我们的关注点转向了铁电体系和磁性体系的传统有效哈密顿量方法,以及这些方法在外场下的扩展和应用。最后介绍了神经网络在处理外场下周期性体系的应用和发展情况,我们坚信这项技术在未来将会有更多突破和发展。
通过对当前研究的全面回顾,我们发现,当前的外场下DFT计算方法仍存在诸多挑战和不足。有限电场方法受制于k点采样的限制,且无法突破布洛赫定理的框架;有限轨道磁场的计算方法尚处于起步阶段,主要由于缺乏适宜的基函数和交换关联泛函近似。我们预见,外场下DFT方法的后续研究可能会集中在开发新的基函数和交换关联泛函近似,同时赝势对于外场响应的研究也可能成为未来的研究焦点。值得我们注意的是,静态DFT并非是研究外场对物质作用的唯一方法。含时密度泛函理论(TDDFT)[238,239],尤其是含时电流-密度泛函理论(TDCDFT)[240],可能提供了一个更为自然的框架来描述外场与物质的相互作用。过去十年中,TDDFT已经取得了显著的进展,我们预期TDDFT和TDCDFT的进一步发展及其与机器学习技术的结合将是研究周期性体系在外加电磁场下行为的有效工具。
参考文献
[1] Hohenberg P, Kohn W 1964 Phys. Rev. 136 B864
[2] Kohn W 1999 Rev. Mod. Phys. 71 1253
[3] Kohn W, Sham L J 1965 Phys. Rev. 140 A1133
[4] Wu M 2021 Nat. Rev. Phys. 3 726
[5] Belov K P, Levitin R Z, Nikitin S A 1964 Sov. Phys. Uspekhi 7 179
[6] Haider T 2017 Int. J. Electromagn. Appl. 7 17
[7] Hirohata A, Yamada K, Nakatani Y, Prejbeanu I L, Diény B, Pirro P, Hillebrands B 2020 J. Magn. Magn. Mater. 509 166711
[8] Vitale S A, Nezich D, Varghese J O, Kim P, Gedik N, Jarillo‐Herrero P, Xiao D, Rothschild M 2018 Small 14 1801483
[9] Yao C, Ma Y 2021 Science 24 102541
[10] Spaldin N A, Ramesh R 2019 Nat. Mater. 18 203
[11] Paras, Yadav K, Kumar P, Teja D R, Chakraborty S, Chakraborty M, Mohapatra S S, Sahoo A, Chou M M C, Liang C T, Hang D R 2023 Nanomaterials 13 160
[12] Ennen I, Kappe D, Rempel T, Glenske C, Hütten A 2016 Sensors 16 904
[13] von Klitzing K, Chakraborty T, Kim P, Madhavan V, Dai X, McIver J, Tokura Y, Savary L, Smirnova D, Rey A M, Felser C, Gooth J, Qi X 2020 Nat. Rev. Phys. 2 397
[14] Zhang L, Ren J, Wang J S, Li B 2011 J. Phys. Condens. Matter 23 305402
[15] Baroni S, Giannozzi P, Testa A 1987 Phys. Rev. Lett. 58 1861
[16] Gonze X, Allan D C, Teter M P 1992 Phys. Rev. Lett. 68 3603
[17] Gonze X 1997 Phys. Rev. B 55 10337
[18] Resta R 1992 Ferroelectrics 136 51
[19] King-Smith R D, Vanderbilt D 1993 Phys. Rev. B 47 1651
[20] Resta R 1994 Rev. Mod. Phys. 66 899
[21] Vanderbilt D, King-Smith R D 1993 Phys. Rev. B 48 4442
[22] Resta R 2010 J. Phys. Condens. Mat. 22 123201
[23] Marzari N, Vanderbilt D 1997 Phys. Rev. B 56 12847
[24] Marzari N, Mostofi A A, Yates J R, Souza I, Vanderbilt D 2012 Rev. Mod. Phys. 84 1419
[25] Ortiz G, Martin R M 1994 Phys. Rev. B 49 14202
[26] Resta R 1998 Phys. Rev. Lett. 80 1800
[27] Valença Ferreira De Aragão E, Moreno D, Battaglia S, Bendazzoli G L, Evangelisti S, Leininger T, Suaud N, Berger J A 2019 Phys. Rev. B 99 205144
[28] Nunes R W, Gonze X 2001 Phys. Rev. B 63 155107
[29] Kane E O 1960 J. Phys. Chem. Solids 12 181
[30] Wannier G H 1960 Phys. Rev. 117 432
[31] Nenciu G 1991 Rev. Mod. Phys. 63 91
[32] Souza I, Íñiguez J, Vanderbilt D 2002 Phys. Rev. Lett. 89 117602
[33] Umari P, Pasquarello A 2002 Phys. Rev. Lett. 89 157602
[34] Ymeri H M 1997 Electr. Eng. 80 163
[35] Payne M C, Teter M P, Allan D C, Arias T A, Joannopoulos J D 1992 Rev. Mod. Phys. 64 1045
[36] Fu H, Bellaiche L 2003 Phys. Rev. Lett. 91 057601
[37] Xu C, Chen P, Tan H, Yang Y, Xiang H, Bellaiche L 2020 Phys. Rev. Lett. 125 037203
[38] Chen L, Xu C, Tian H, Xiang H, Íñiguez J, Yang Y, Bellaiche L 2019 Phys. Rev. Lett. 122 247701
[39] Kresse G, Furthmüller J 1996 Phys. Rev. B 54 11169
[40] Giannozzi P, Baroni S, Bonini N, et al. 2009 J. Phys. Condens. Mat. 21 395502
[41] Gonze X, Amadon B, Anglade P M, et al. 2009 Comput. Phys. Commun. 180 2582
[42] Zwanziger J W, Galbraith J, Kipouros Y, Torrent M, Giantomassi M, Gonze X 2012 Comput. Mater. Sci. 58 113
[43] Wu X, Vanderbilt D, Hamann D R 2005 Phys. Rev. B 72 035105
[44] Vanderbilt D 2000 J. Phys. Chem. Solids 61 147
[45] Bennett D, Tanner D, Ghosez P, Janolin P E, Bousquet E 2022 Phys. Rev. B 106 174105
[46] Fiebig M, Lottermoser T, Meier D, Trassin M 2016 Nat. Rev. Mater. 1 16046
[47] Malashevich A, Coh S, Souza I, Vanderbilt D 2012 Phys. Rev. B 86 094430
[48] Gonze X, Ghosez Ph, Godby R W 1995 Phys. Rev. Lett. 74 4035
[49] Resta R 2018 Eur. Phys. J. B 91 100
[50] Stengel M, Spaldin N A, Vanderbilt D 2009 Nat. Phys. 5 304
[51] Hong J, Vanderbilt D 2011 Phys. Rev. B 84 115107
[52] Jiang Z, Zhang R, Li F, Jin L, Zhang N, Wang D, Jia C L 2016 AIP Adv. 6 065122
[53] Wu X, Rabe K M, Vanderbilt D 2011 Phys. Rev. B 83 020104
[54] Wu X, Stengel M, Rabe K M, Vanderbilt D 2008 Phys. Rev. Lett. 101 087601
[55] Stengel M, Fennie C J, Ghosez P 2012 Phys. Rev. B 86 094112
[56] Stengel M, Vanderbilt D 2009 Phys. Rev. B 80 241103
[57] Stengel M 2011 Phys. Rev. Lett. 106 136803
[58] Cancellieri C, Fontaine D, Gariglio S, Reyren N, Caviglia A D, Fête A, Leake S J, Pauli S A, Willmott P R, Stengel M, Ghosez Ph, Triscone J M 2011 Phys. Rev. Lett. 107 056102
[59] Hong J, Vanderbilt D 2013 Phys. Rev. B 88 174107
[60] Diéguez O, Vanderbilt D 2006 Phys. Rev. Lett. 96 056401
[61] Barth U V, Hedin L 1972 J. Phys. C Solid State Phys. 5 1629
[62] Gunnarsson O, Lundqvist B I 1976 Phys. Rev. B 13 4274
[63] Kubler J, Hock K H, Sticht J, Williams A R 1988 J. Phys. F Met. Phys. 18 469
[64] Sharma S, Dewhurst J K, Ambrosch-Draxl C, Kurth S, Helbig N, Pittalis S, Shallcross S, Nordström L, Gross E K U 2007 Phys. Rev. Lett. 98 196405
[65] Sandratskii L M 1998 Adv. Phys. 47 91
[66] Pu Z C, Li H, Zhang N, Jiang H, Gao Y Q, Xiao Y Q, Gao Y Q, Sun Q M, Zhang Y, Shao S H 2023 Phys. Rev. Res. 5 013036
[67] Ullrich C A 2018 Phys. Rev. B 98 035140
[68] Jacob C R, Reiher M 2012 Int. J. Quantum Chem. 112 3661
[69] Ullrich C A 2019 Phys. Rev. A 100 012516
[70] Bousquet E, Spaldin N A, Delaney K T 2011 Phys. Rev. Lett. 106 107202
[71] Bousquet E, Spaldin N 2011 Phys. Rev. Lett. 107 197603
[72] Dasa T R, Hao L, Liu J, Xu H 2019 J. Mater. Chem. C 7 13294
[73] Vignale G, Rasolt M 1987 Phys. Rev. Lett. 59 2360
[74] Vignale G, Rasolt M, Geldart D J W 1990 Advanced Quantum Chemistry (Cambridge: Academic Press) pp235–253
[75] Laestadius A 2014 Int. J. Quantum Chem. 114 1445
[76] Laestadius A, Benedicks M 2014 Int. J. Quantum Chem. 114 782
[77] Laestadius A 2014 J. Math. Chem. 52 2581
[78] Grayce C J, Harris R A 1994 Phys. Rev. A 50 3089
[79] Reimann S, Borgoo A, Tellgren E I, Teale A M, Helgaker T 2017 J. Chem. Theory Comput. 13 4089
[80] Tellgren E I, Teale A M, Furness J W, Lange K K, Ekström U, Helgaker T 2014 J. Chem. Phys. 140 034101
[81] Furness J W, Verbeke J, Tellgren E I, Stopkowicz S, Ekström U, Helgaker T, Teale A M 2015 J. Chem. Theory Comput. 11 4169
[82] Reimann S, Borgoo A, Austad J, Tellgren E I, Teale A M, Helgaker T, Stopkowicz S 2019 Mol. Phys. 117 97
[83] Sen S, Tellgren E I 2021 J. Chem. Theory Comput. 17 1480
[84] Pemberton M J, Irons T J P, Helgaker T, Teale A M 2022 J. Chem. Phys. 156 204113
[85] Penz M, Tellgren E I, Csirik M A, Ruggenthaler M, Laestadius A 2023 arXiv: 2303.01357 [quant-ph]
[86] Lieb E H, Schrader R 2013 Phys. Rev. A 88 032516
[87] Diener G 1991 J. Phys. Condens. Mat. 3 9417
[88] Pan X Y, Sahni V 2010 Int. J. Quantum Chem. 110 2833
[89] Tellgren E I, Kvaal S, Sagvolden E, Ekström U, Teale A M, Helgaker T 2012 Phys. Rev. A 86 062506
[90] Laestadius A, Benedicks M 2015 Phys. Rev. A 91 032508
[91] Laestadius A, Penz M, Tellgren E I 2021 J. Phys. Condens. Mat. 33 295504
[92] Thonhauser T, Ceresoli D, Mostofi A A, Marzari N, Resta R, Vanderbilt D 2009 J. Chem. Phys. 131 101101
[93] Ceresoli D, Gerstmann U, Seitsonen A P, Mauri F 2010 Phys. Rev. B 81 060409
[94] Murakami S 2006 Phys. Rev. Lett. 97 236805
[95] Coh S, Vanderbilt D, Malashevich A, Souza I 2011 Phys. Rev. B 83 085108
[96] Göbel B, Mook A, Henk J, Mertig I 2019 Phys. Rev. B 99 060406
[97] Essin A M, Moore J E, Vanderbilt D 2009 Phys. Rev. Lett. 102 146805
[98] Essin A M, Turner A M, Moore J E, Vanderbilt D 2010 Phys. Rev. B 81 205104
[99] Thonhauser T 2011 Int. J. Mod. Phys. B 25 1429
[100] Xiao D, Shi J, Niu Q 2005 Phys. Rev. Lett. 95 137204
[101] Aryasetiawan F, Karlsson K, Miyake T 2016 Phys. Rev. B 93 161104
[102] Ceresoli D, Thonhauser T, Vanderbilt D, Resta R 2006 Phys. Rev. B 74 024408
[103] Aryasetiawan F, Karlsson K 2019 J. Phys. Chem. Solids 128 87
[104] Thonhauser T, Ceresoli D, Vanderbilt D, Resta R 2005 Phys. Rev. Lett. 95 137205
[105] Shi J, Vignale G, Xiao D, Niu Q 2007 Phys. Rev. Lett. 99 197202
[106] Lopez M G, Vanderbilt D, Thonhauser T, Souza I 2012 Phys. Rev. B 85 014435
[107] Hanke J P, Freimuth F, Nandy A K, Zhang H, Blügel S, Mokrousov Y 2016 Phys. Rev. B 94 121114
[108] Pickard C J, Mauri F 2001 Phys. Rev. B 63 245101
[109] Yates J R, Pickard C J, Mauri F 2007 Phys. Rev. B 76 024401
[110] Qiao S, Kimura A, Adachi H, Iori K, Miyamoto K, Xie T, Namatame H, Taniguchi M, Tanaka A, Muro T, Imada S, Suga S 2004 Phys. Rev. B 70 134418
[111] Kolchinskaya A, Komissinskiy P, Yazdi M B, Vafaee M, Mikhailova D, Narayanan N, Ehrenberg H, Wilhelm F, Rogalev A, Alff L 2012 Phys. Rev. B 85 224422
[112] Cai W, Galli G 2004 Phys. Rev. Lett. 92 186402
[113] Lee E, Cai W, Galli G A 2007 J. Comput. Phys. 226 1310
[114] Kohn W 1959 Phys. Rev. 115 1460
[115] Zak J 1964 Phys. Rev. 134 A1602
[116] Xu K, Feng J, Xiang H 2022 Chin. Phys. B 31 097505
[117] Drautz R, Fähnle M 2004 Phys. Rev. B 69 104404
[118] Hastings W K 1972 Biometrika 57 97
[119] Gilbert T L 2004 IEEE Trans. Magn. 40 3443
[120] Tranchida J, Plimpton S J, Thibaudeau P, Thompson A P 2018 J. Comput. Phys. 372 406
[121] Rózsa L, Udvardi L, Szunyogh L 2013 J. Phys. Condens. Mat. 25 506002
[122] Rózsa L, Udvardi L, Szunyogh L 2014 J. Phys. Condens. Mat. 26 216003
[123] Ma P W, Dudarev S L, Woo C H 2012 Phys. Rev. B 85 184301
[124] Ma P W, Woo C H, Dudarev S L 2008 Phys. Rev. B 78 024434
[125] Liechtenstein A I, Anisimov V I, Zaanen J 1995 Phys. Rev. B 52 R5467
[126] Dudarev S L, Botton G A, Savrasov S Y, Humphreys C J, Sutton A P 1998 Phys. Rev. B 57 1505
[127] Himmetoglu B, Floris A, De Gironcoli S, Cococcioni M 2014 Int. J. Quantum Chem. 114 14
[128] Dederichs P H, Blügel S, Zeller R, Akai H 1984 Phys. Rev. Lett. 53 2512
[129] Ma P W, Dudarev S L 2015 Phys. Rev. B 91 054420
[130] Chen Y, Yang Y, Xu C, Xiang H 2023 Phys. Rev. B 107 214439
[131] Cai Z, Wang K, Xu Y, Wei S H, Xu B 2023 arXiv: 2208.04551 [cond-mat]
[132] Li X, Yu H, Lou F, Feng J, Whangbo M H, Xiang H 2021 Molecules 26 803
[133] Xu C, Xu B, Dupé B, Bellaiche L 2019 Phys. Rev. B 99 104420
[134] Xu C, Feng J, Prokhorenko S, Nahas Y, Xiang H, Bellaiche L 2020 Phys. Rev. B 101 060404
[135] Kitaev A 2006 Ann. Phys. 321 2
[136] Dzyaloshinsky I 1958 J. Phys. Chem. Solids 4 241
[137] Moriya T 1960 Phys. Rev. 120 91
[138] Moriya T 1960 Phys. Rev. Lett. 4 228
[139] Fert A, Cros V, Sampaio J 2013 Nat. Nanotechnol. 8 152
[140] Bak P, Jensen M H 1980 J. Phys. C Solid State Phys. 13 L881
[141] Yu X Z, Kanazawa N, Onose Y, Kimoto K, Zhang W Z, Ishiwata S, Matsui Y, Tokura Y 2011 Nat. Mater. 10 106
[142] Weber T, Waizner J, Tucker G S, Georgii R, Kugler M, Bauer A, Pfleiderer C, Garst M, Böni P 2018 Phys. Rev. B 97 224403
[143] Huang S X, Chien C L 2012 Phys. Rev. Lett. 108 267201
[144] Fujishiro Y, Kanazawa N, Tokura Y 2020 Appl. Phys. Lett. 116 090501
[145] Pappas C, Lelièvre-Berna E, Falus P, Bentley P M, Moskvin E, Grigoriev S, Fouquet P, Farago B 2009 Phys. Rev. Lett. 102 197202
[146] Ni J Y, Li X Y, Amoroso D, He X, Feng J S, Kan E J, Picozzi S, Xiang H J 2021 Phys. Rev. Lett. 127 247204
[147] Grytsiuk S, Hanke J P, Hoffmann M, Bouaziz J, Gomonay O, Bihlmayer G, Lounis S, Mokrousov Y, Blügel S 2020 Nat. Commun. 11 511
[148] Kartsev A, Augustin M, Evans R F L, Novoselov K S, Santos E J G 2020 Npj Comput. Mater. 6 150
[149] Zhu H F, Cao H Y, Xie Y, Hou Y S, Chen S, Xiang H, Gong X G 2016 Phys. Rev. B 93 024511
[150] Novák P, Chaplygin I, Seifert G, Gemming S, Laskowski R 2008 Comput. Mater. Sci. 44 79
[151] Fedorova N S, Ederer C, Spaldin N A, Scaramucci A 2015 Phys. Rev. B 91 165122
[152] Xiang H, Lee C, Koo H J, Gong X, Whangbo M H 2013 Dalton. Trans. 42 823
[153] Xiang H J, Kan E J, Wei S H, Whangbo M H, Gong X G 2011 Phys. Rev. B 84 224429
[154] Li X Y, Lou F, Gong X G, Xiang H 2020 New J. Phys. 22 053036
[155] Lou F, Li X Y, Ji J Y, Yu H Y, Feng J S, Gong X G, Xiang H J 2021 J. Chem. Phys. 154 114103
[156] Lounis S, Dederichs P H 2010 Phys. Rev. B 82 180404
[157] Szilva A, Costa M, Bergman A, Szunyogh L, Nordström L, Eriksson O 2013 Phys. Rev. Lett. 111 127204
[158] He X, Helbig N, Verstraete M J, Bousquet E 2021 Comput. Phys. Commun. 264 107938
[159] Katsnelson M I, Kvashnin Y O, Mazurenko V V, Lichtenstein A I 2010 Phys. Rev. B 82 100403
[160] Katsnelson M I, Lichtenstein A I 2000 Phys. Rev. B 61 8906
[161] Liechtenstein A I, Katsnelson M I, Antropov V P, Gubanov V A 1987 J. Magn. Magn. Mater. 67 65
[162] Wang X, Wang D sheng, Wu R, Freeman A J 1996 J. Magn. Magn. Mater. 159 337
[163] Wan X, Yin Q, Savrasov S Y 2006 Phys. Rev. Lett. 97 266403
[164] Durhuus F L, Skovhus T, Olsen T 2023 J. Phys. Condens. Mat. 35 105802
[165] Bhowmik T K, Sinha T P 2021 J. Solid State Chem. 304 122570
[166] Campbell D, Xu C, Bayaraa T, Bellaiche L 2020 Phys. Rev. B 102 144406
[167] Polesya S, Mankovsky S, Bornemann S, Ködderitzsch D, Minár J, Ebert H 2014 Phys. Rev. B 89 184414
[168] Dupé B, Hoffmann M, Paillard C, Heinze S 2014 Nat. Commun. 5 4030
[169] Simon E, Palotás K, Rózsa L, Udvardi L, Szunyogh L 2014 Phys. Rev. B 90 094410
[170] Fernandes I L, Chico J, Lounis S 2020 J. Phys. Condens. Mat. 32 425802
[171] Liang J, Wang W, Du H, Hallal A, Garcia K, Chshiev M, Fert A, Yang H 2020 Phys. Rev. B 101 184401
[172] Carvalho P C, Miranda I P, Klautau A B, Bergman A, Petrilli H M 2021 Phys. Rev. Mater. 5 124406
[173] Zhang Y, Xu C, Cheng P, Nahas Y, Prokhorenko S, Bellaiche L 2020 Phys. Rev. B 102 241107
[174] Leonov A O, Mostovoy M 2015 Nat. Commun. 6 8275
[175] Xu C, Feng J, Xiang H, Bellaiche L 2018 npj Comput. Mater. 4 1
[176] Cochran W 1960 Adv. Phys. 9 387
[177] Blinc R 1987 Ferroelectrics 74 301
[178] Zhong W, Vanderbilt D, Rabe K M 1994 Phys. Rev. Lett. 73 1861
[179] Zhong W, Vanderbilt D, Rabe K M 1995 Phys. Rev. B 52 6301
[180] LmEs M E, Bel I 1969 Phys. Rev. 177
[181] Rabe K M, Joannopoulos J D 1987 Phys. Rev. Lett. 59 570
[182] Rabe K M, Joannopoulos J D 1987 Phys. Rev. B 36 6631
[183] Rabe K M, Waghmare U V 1995 Phys. Rev. B 52 13236
[184] Bellaiche L, García A, Vanderbilt D 2000 Phys. Rev. Lett. 84 5427
[185] Walizer L, Lisenkov S, Bellaiche L 2006 Phys. Rev. B 73 144105
[186] Vanderbilt D, Zhong W 1998 Ferroelectrics 206 181
[187] Kornev I A, Bellaiche L, Janolin P E, Dkhil B, Suard E 2006 Phys. Rev. Lett. 97 157601
[188] Fthenakis Z G, Ponomareva I 2017 Phys. Rev. B 96 184110
[189] Mani B K, Lisenkov S, Ponomareva I 2015 Phys. Rev. B 91 134112
[190] Wang P S, Xiang H J 2014 Phys. Rev. X 4 011035
[191] Ye Q J, Zhang X F, Li X Z 2019 Electron. Struct. 1 044006
[192] Nahas Y, Prokhorenko S, Louis L, Gui Z, Kornev I, Bellaiche L 2015 Nat. Commun. 6 8542
[193] Ponomareva I, Lisenkov S 2012 Phys. Rev. Lett. 108 167604
[194] Fan N, Íñiguez J, Bellaiche L, Xu B 2022 Phys. Rev. B 106 224107
[195] Ma X, Yang Y, Bellaiche L, Wu D 2022 Phys. Rev. B 105 054104
[196] Zhang J T, Hou X, Zhang Y J, Tang G, Wang J 2021 Mater. Rep. Energy 1 100050
[197] Ponomareva I, Tagantsev A K, Bellaiche L 2012 Phys. Rev. B 85 104101
[198] Lai B K, Ponomareva I, Naumov I I, Kornev I, Fu H, Bellaiche L, Salamo G J 2006 Phys. Rev. Lett. 96 137602
[199] Mani B K, Herchig R, Glazkova E, Lisenkov S, Ponomareva I 2016 Nanotechnology 27 195705
[200] Lisenkov S, Ponomareva I 2009 Phys. Rev. B 80 140102
[201] Beckman S P, Wan L F, Barr J A, Nishimatsu T 2012 Mater. Lett. 89 254
[202] Tarnaoui M, Zaim N, Kerouad M, Zaim A 2020 Comput. Mater. Sci. 183 109816
[203] Fu H, Bellaiche L 2003 Phys. Rev. Lett. 91 257601
[204] Prosandeev S, Ponomareva I, Kornev I, Naumov I, Bellaiche L 2006 Phys. Rev. Lett. 96 237601
[205] Sasani A, Íñiguez J, Bousquet E 2022 Phys. Rev. B 105 064414
[206] Kornev I A, Lisenkov S, Haumont R, Dkhil B, Bellaiche L 2007 Phys. Rev. Lett. 99 227602
[207] Lisenkov S, Kornev I A, Bellaiche L 2009 Phys. Rev. B 79 012101
[208] Albrecht D, Lisenkov S, Ren W, Rahmedov D, Kornev I A, Bellaiche L 2010 Phys. Rev. B 81 140401
[209] Rahmedov D, Wang D, Íñiguez J, Bellaiche L 2012 Phys. Rev. Lett. 109 037207
[210] Jin G, Cao K, Guo G C, He L 2012 Phys. Rev. Lett. 108 187205
[211] Xu B, Dupé B, Xu C, Xiang H, Bellaiche L 2018 Phys. Rev. B 98 184420
[212] Bhattacharjee S, Rahmedov D, Wang D, Íñiguez J, Bellaiche L 2014 Phys. Rev. Lett. 112 147601
[213] Xiang H J, Kan E J, Zhang Y, Whangbo M H, Gong X G 2011 Phys. Rev. Lett. 107 157202
[214] Lu X Z, Wu X, Xiang H J 2015 Phys. Rev. B 91 100405
[215] Xiang H J, Wang P S, Whangbo M H, Gong X G 2013 Phys. Rev. B 88 054404
[216] Wang P S, Lu X Z, Gong X G, Xiang H J 2016 Comput. Mater. Sci. 112 448
[217] Pi M, Xu X, He M, Chai Y 2022 Phys. Rev. B 105 L020407
[218] Behler J 2011 J. Chem. Phys. 134 074106
[219] Himanen L, Jäger M O J, Morooka E V, Federici Canova F, Ranawat Y S, Gao D Z, Rinke P, Foster A S 2020 Comput. Phys. Commun. 247 106949
[220] Liu J, Luo W, Wang L, Zhang J, Fu X Z, Luo J L 2022 Adv. Funct. Mater. 32 2110748
[221] Huo H, Rupp M 2022 Mach. Learn. Sci. Technol. 3 045017
[222] Isayev O, Oses C, Toher C, Gossett E, Curtarolo S, Tropsha A 2017 Nat. Commun. 8 15679
[223] Zhang L, Han J, Wang H, Car R, E W 2018 Phys. Rev. Lett. 120 143001
[224] Ren Z, Tian S I P, Noh J, Oviedo F, Xing G, Li J, Liang Q, Zhu R, Aberle A G, Sun S, Wang X, Liu Y, Li Q, Jayavelu S, Hippalgaonkar K, Jung Y, Buonassisi T 2022 Matter 5 314
[225] Xie T, Fu X, Ganea O E, Barzilay R, Jaakkola T 2022 arXiv: 2110.06197 [cond-mat]
[226] Xie T, Grossman J C 2018 Phys. Rev. Lett. 120 145301
[227] Wang Q, Zhang L 2021 Nat. Commun. 12 5359
[228] Schütt K T, Sauceda H E, Kindermans P J, Tkatchenko A, Müller K R 2018 J. Chem. Phys. 148 241722
[229] Yu H, Zhong Y, Hong L, Xu C, Ren W, Gong X, Xiang H 2023 arXiv: 2203.02853 [cond-mat]
[230] Weiler M, Geiger M, Welling M, Boomsma W, Cohen T 2018 arXiv: 1807.02547 [cs, stat]
[231] Batzner S, Musaelian A, Sun L, Geiger M, Mailoa J P, Kornbluth M, Molinari N, Smidt T E, Kozinsky B 2022 Nat. Commun. 13 2453
[232] Musaelian A, Batzner S, Johansson A, Sun L, Owen C J, Kornbluth M, Kozinsky B 2023 Nat. Commun. 14 579
[233] Kondor R 2018 arXiv: 1803.01588 [cs]
[234] Thomas N, Smidt T, Kearnes S, Yang L, Li L, Kohlhoff K, Riley P 2018 arXiv: 1802.08219 [cs]
[235] Yu H Y, Zhong Y, Ji J Y, Gong X G, Xiang H J 2022 arXiv: 2211.11403 [cond-mat]
[236] Ma L Y, Wu J, Zhu T Y, Huang Y W, Lu Q Y, Liu S 2023 arXiv: 2305.02952 [cond-mat]
[237] Zhang L F, Chen M H, Wu X F, Wang H, Weinan E, Car R 2020 Phys. Rev. B 102 041121
[238] Marques M A L, Gross E K U 2004 Annu. Rev. Phys. Chem. 55 427
[239] Botti S, Schindlmayr A, Sole R D, Reining L 2007 Rep. Prog. Phys. 70 357
[240] Romaniello P, De Boeij P L 2005 Phys. Rev. B 71 155108
(参考文献可上下滑动查看)

https://wap.sciencenet.cn/blog-3427348-1428891.html
上一篇:90周年专栏 | 月球玻璃
下一篇:专题 | 生物分子模拟中的机器学习