空间自相关(spatial autocorrelation)是指一些变量在同一个分布区内的观测数据之间潜在的相互依赖性。Tobler(1970)曾指出“地理学第一定律：任何东西与别的东西之间都是相关的，但近处的东西比远处的东西相关性更强”。

    在地理统计学科中应用较多，现已有多种指数可以使用，但最主要的有两种指数，即Moran的I指数和Geary的C指数。

下面介绍了：相关 -> 时间维自相关 -> 空间自相关

摘自wikipedia: https://en.wikipedia.org/wiki/Autocorrelation

相关

Different fields of study define autocorrelation differently, and not all of these definitions are equivalent. In some fields, the term is used interchangeably with autocovariance.

In statistics, the autocorrelation of a random process describes the correlation between values of the process at different times, as a function of the two times or of the time lag. Let X be some repeatable process, and i be some point in time after the start of that process. (i may be an integerfor a discretetime process or a real number for a continuoustime process.) Then X_i is the value (or realization) produced by a given run of the process at time i. Suppose that the process is further known to have defined values for mean μ_i and variance σ_i² for all times i. Then the definition of the autocorrelation between times s and t is

where "E" is the expected value operator. Note that this expression is not well-defined for all time series or processes, because the variance may be zero (for a constant process) or infinite (for processes with distribution lacking well-behaved moments, such as certain types of power law). If the function R is well-defined, its value must lie in the range [−1, 1], with 1 indicating perfect correlation and −1 indicating perfect anti-correlation.

时间自相关

If X_t is a widesense stationary process then the mean μ and the variance σ² are timeindependent, and further the autocorrelation depends only on the lag between t and s: the correlation depends only on the timedistance between the pair of values but not on their position in time. This further implies that the autocorrelation can be expressed as a function of the timelag, and that this would be an even function of the lagτ = s − t. This gives the more familiar form

and the fact that this is an even function can be stated as

It is common practice in some disciplines, other than statistics and time series analysis, to drop the normalization by σ² and use the term "autocorrelation" interchangeably with "autocovariance". However, the normalization is important both because the interpretation of the autocorrelation as a correlation provides a scalefree measure of the strength of statistical dependence, and because the normalization has an effect on the statistical properties of the estimated autocorrelations.

空间自相关

Spatial autocorrelation statistics measure and analyze the degree of dependency among observations in a geographic space. Classic spatial autocorrelation statistics include Moran's , Geary's 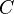, Getis's  and the standard deviational ellipse. These statistics require measuring a spatial weights matrix that reflects the intensity of the geographic relationship between observations in a neighborhood, e.g., the distances between neighbors, the lengths of shared border, or whether they fall into a specified directional class such as "west". Classic spatial autocorrelation statistics compare the spatial weights to the covariance relationship at pairs of locations. Spatial autocorrelation that is more positive than expected from random indicate the clustering of similar values across geographic space, while significant negative spatial autocorrelation indicates that neighboring values are more dissimilar than expected by chance, suggesting a spatial pattern similar to a chess board.

Spatial autocorrelation statistics such as Moran's and Geary's 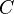are global in the sense that they estimate the overall degree of spatial autocorrelation for a dataset. The possibility of spatial heterogeneity suggests that the estimated degree of autocorrelation may vary significantly across geographic space. Local spatial autocorrelation statistics provide estimates disaggregated to the level of the spatial analysis units, allowing assessment of the dependency relationships across space. statistics compare neighborhoods to a global average and identify local regions of strong autocorrelation. Local versions of the and 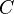statistics are also available.

In statistics, Moran's I is a measure of spatial autocorrelation developed by Patrick Alfred Pierce Moran.Spatial autocorrelation is characterized by a correlation in a signal among nearby locations in space. Spatial autocorrelation is more complex than onedimensional autocorrelation because spatial correlation is multidimensional (i.e. 2 or 3 dimensions of space) and multi-directional.

Moran's I is defined as

where is the number of spatial units indexed by and ; is the variable of interest; is the mean of ; and is an element of a matrix of spatial weights.

The expected value of Moran's I under the null hypothesis of no spatial autocorrelation is

Its variance equals

where

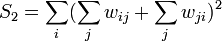
^[3] Negative values indicate negative spatial autocorrelation and the inverse for positive values. Values range from −1 (indicating perfect dispersion) to +1 (perfect correlation). A zero value indicates a random spatial pattern. For statistical hypothesis testing, Moran's I values can be transformed to Z-scores in which values greater than 1.96 or smaller than −1.96 indicate spatial autocorrelation that is significant at the 5% level.

Moran's I is inversely related to Geary's C, but it is not identical. Moran's I is a measure of global spatial autocorrelation, while Geary's C is more sensitive to local spatial autocorrelation.