学习笔记-爱因斯坦1905年文章/1926年翻译的英文版

前不久，关于布朗运动问题的讨论相当热烈。为了弄清思路，最好是先读读原文。于是在网上下载了爱因斯坦1905年文章/1926年翻译成英文版的“关于布朗运动理论的研究-I (Investigations on the Theory of Brownian Movement)”。以及维纳1923年发表的代表性文章“微分空间(Differential-Space)”。本文是读爱因斯坦文章的学习笔记。 

网上下载的原文是影印图片，不仅不方便阅读，而且有明显缺陷。因此整理成Word文件，花了不少功夫。例如，爱因斯坦的文章英文版，网上找到了两个来源，例如图中左侧版本有多处阅读记录，影印质量较差。右侧版本比较整齐清楚。但都有方程出错状况，如在第14页上：

虽然整理英文版到Word文件，不仅要核对文字，而且输入各个方程，很花时间。但整理过程也是学习，较容易理解作者的意图和解释。之后为了便于讨论，还请DeepSeek在此Word文件基础上翻译成中文。继而也要整理一遍。因此得到初步学习笔记：

 爱因斯坦文章副标题是：根据分子热运动理论，研究静止液体中悬浮微粒的运动。分5个章节：

§1. 关于作用于悬浮粒子的渗透压

§2 从分子热运动理论看渗透压

§3 悬浮小球的扩散理论

§4 论液体中悬浮粒子的不规则运动及其与扩散的关系

§5 悬浮粒子平均位移的公式，测定原子实际大小的新方法

从文章可见：

1、 当年爱因斯坦的研究目的，是确认发生布朗运动的起因是载体分子热运动，因此为分子热运动理论提供证据。并证实分子和原子的客观存在。

2、 从5个章节的标题看，研究着重分子物理，如渗透压和测定原子实际大小等。对于布朗粒子，针对的是悬浮粒子的扩散理论，以及不规则运动和扩散的关系。

3、 关于布朗粒子，文中研究的是大量粒子的集体行为，即总数为的粒子，因为不规则运动，其空间分布（假设一维）随时间变化的粒子数分布函数。

爱因斯坦假设：每个单个粒子的运动和所有其他粒子互相独立；并且同一个粒子在不同时间间隔后的运动，只要这些时间间隔选择得不是太小，就必须被视为是相互独立的过程。

于是用统计方法，推导得到著名的扩散方程，其中是扩散系数：

并得到了“精确解”正态分布：

计算得到这些粒子的平均位移随时间的变化：

还推得扩散系数为（为小球直径）

从上一式消去，得到：

（式中R-气体常数，N-阿伏伽德罗常数，k-玻尔兹曼常数）

还设想一个环境条件，计算得到直径为1微米的粒子，在摄氏17度水体中，1分钟内粒子的平均位移近似为0.8微米。 

4、 爱因斯坦文章的结论中说，在文章发表后，别的科学家告诉他，已经通过直接观测确认：布朗运动是由液体分子不规则的热运动引起的。因此证明了他自己工作的正确性。

 学习文章可见，爱因斯坦研究重点是大量布朗粒子运动的统计性质。得到的“精确解”是粒子数随时间在空间的统计分布。根据正态分布可以画出粒子数浓度随时间变化的曲线，但不能画出任何一个粒子的运动轨迹。因此，不能说爱因斯坦引入了所有布朗粒子在时刻的位置（随机变量）：

爱因斯坦1905年的工作假设了大量布朗粒子的运动互相独立，同一布朗粒子在不同时段的运动之间也互相独立。但是从爱因斯坦给出的正态分布是粒子分布浓度的“解析解”，无法探讨单个布朗粒子的随机运动。即无法跟踪单个粒子的运动轨迹，或讨论其速度变化。 

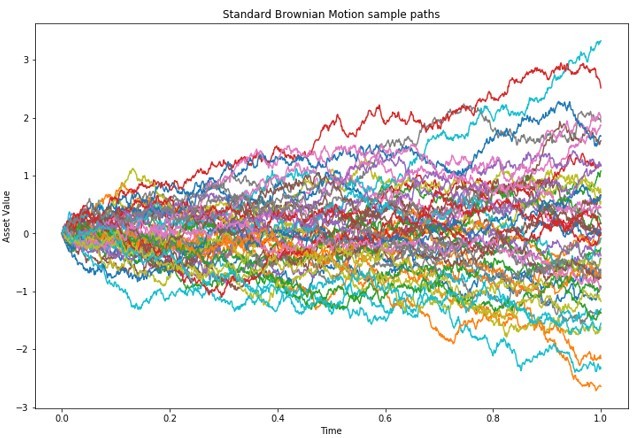
网上可以找到多个布朗粒子运动轨迹，例如下图含50条轨迹。是模拟“标准布朗运动”得到的。从前一阵有关讨论可知，标准布朗运动指的就是维纳随机过程。即对维纳过程而言，才是

图片出处：https://www.quantstart.com/articles/brownian-motion-simulation-with-python/

附件：

1905爱因斯坦文章英文-我整理交DeepSeek翻译.docx

1905爱因斯坦文章1926译成英文.pdf

1905爱因斯坦文章DeepSeek翻译-经过我整理.docx