16.13 从agi走向asi

1、一阶谓词

哥德尔不完备定理证明了，任何包含皮亚诺算术的一致性的形式系统，必定存在不可判定命题；或者，形式系统无法证明自身的一致性。

哥德尔证明的关键，是将形式系统中的符号、公式、证明序列映射为自然数（哥德尔数字化同构），使语言逻辑关系转化为算术关系。 通过哥德尔编码，公式G 可表示为算术命题，形成逻辑上自指。形式系统能表示所有递归函数，自指命题构造符合系统语法。若系统不一致，失去数学意义；若系统一致，则自指命题 G 不可判定。

哥德尔定理的前提是“包含皮亚诺算术的形式系统”，皮亚诺形式化系统 的强大之处在于它能定义所有‘原始递归函数’和‘谓词’，哥德尔编码依赖的关键是元数学概念（如“`x` 是公式 `y` 的一个证明”）在系统内可表示为算术谓词。证明论中的基本概念（公式构造、序列操作、证明验证）都是原始递归的或能归约到原始递归过程。因此，它们在皮亚诺形式化系统内是可表示的。

形式系统语法规则： 原子公式 (Atomic Forμla) 有且只能包含一个谓词符号（相当于自然语言的“核心动词”）。形式系统的一个原子公式内不允许出现多个谓词（动词），否则是语法错误。类似的，人类自然语言陈述句中核心动词通常只有一个，比如英语若一句话中出现多个动词，则需要额外介词to或ing等，以便明确哪一个是这句话的核心动词。

所以说，形式逻辑是一阶谓词逻辑的。

数理逻辑的标准形式化工具（一阶谓词逻辑）中的主谓宾结构的清晰对应。 比如，句子 “小明读书” 中，动作的发起者的‘小明’对应主语变元、宾语‘书’对应另一个变元 、谓语‘读’是谓词符号表示二元关系。

皮亚诺公理体系试图用形式化公理覆盖所有算术真理，但是哥德尔证明其算术真理的“自洽性”与“完备性”无法同时满足。皮亚诺系统逻辑链条不完备性体现了形式化表达的本质缺陷。

形式逻辑准确对应一阶逻辑，皮亚诺系统缺陷本质上是一阶逻辑的缺陷。因为一阶逻辑固有缺陷，皮亚诺系统无法表达高阶的系统。

比如，皮亚诺系统无法表达二阶流形的莫比乌斯带。因为莫比乌斯带上的法向量A旋转一周后，同一位置出现了法向量B，向量A和向量B在相同位置但其箭头反向，违反一阶向量场的一致性，逻辑指向相互矛盾，一阶逻辑在二阶流形上无法自洽！

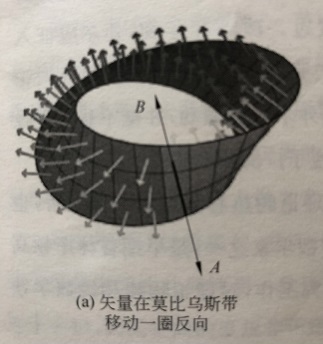
同样的原因，向量空间不能同时测量原空间和对偶空间，位置和动量虽然在复空间（与张量空间表达对等）存在复函数，但是该复函数在向量空间（与实空间表达对等）无法取得不动点，这就是不确定性原理。

2、多头注意力

既然一阶逻辑系统（向量空间）存在固有缺陷，那么高阶逻辑系统（高阶张量空间）是否可以解决完备性缺陷呢？

数理逻辑的标准形式化工具（一阶谓词逻辑）中的主谓宾结构的清晰对应： 比如句子 “小明读书” 中，小明是动作的发起者、描述的对象，主语“小明”对应一个变元(自变量x )、宾语“书”对应一个变元(因变量y ) 、谓语“读”是谓词符号表示二元关系(映射f )。这个句子公式本身没有真值，直到在某个解释（模型）中被赋值。形式化语言“小明读书”原子命题类似函数项 f(x)=y的数理逻辑，函数符号 f 用于构造谓词项。 句子小明读书，“读” 是描述主语动作或状态的核心动词（核心谓语），谓语 ≈ 映射 f ；函数相当于向量，函数 f(x) = y，将输入 x转换为输出 y，f 代表了向量的性质（规则或操作） 。形象而言，形式化语言的主语、谓语、宾语，相当于函数f(x)=y中的自变量x、映射f、因变量y。 在这个层面上类比是直观的， 主语提供输入，谓语施加操作/关系，宾语是操作的结果或关联对象。

问题来了，既然函数 f 相当于向量，那么复合函数 f(g(h(x))) 是否代表高阶张量tensor呢？还有，复合函数与多头注意力机制Transformer有关系吗？

事实上，深度学习AI的多隐层结构数据元tensor（张量）、多重复合函数 f(...g(h(x))...)、多头注意力机制Transformer，三者在深度学习中相互关联、密不可分、缺一不可。

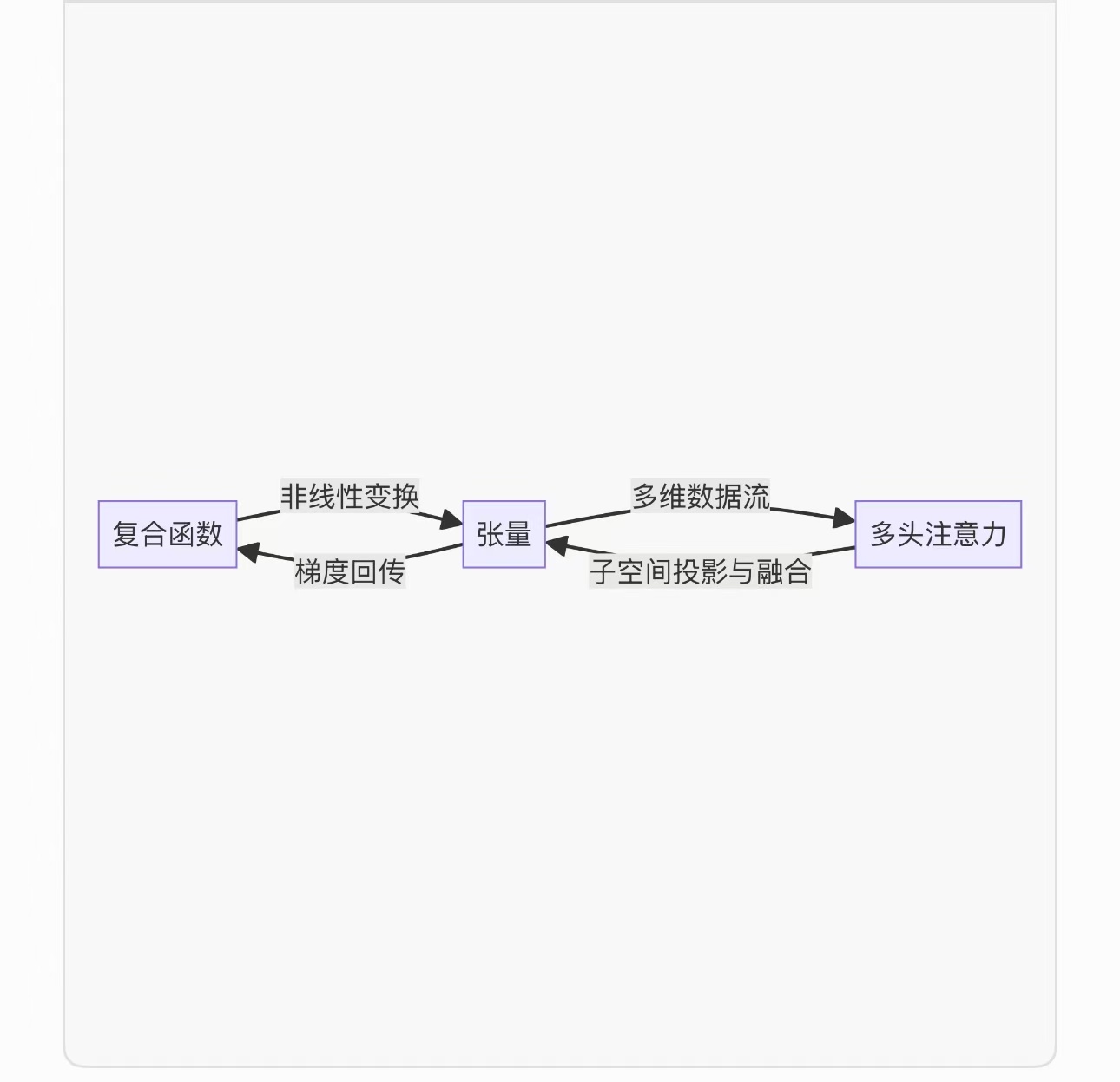
深度学习AI“张量运算”到“智能映射”的本质是Transformer以Tensor为数据基础，通过多头注意力机制构建复合函数的核心组件，深度学习张量（Tensor）、复合函数与多头注意力（Transformer）共同构成了现代深度学习模型的数据载体、计算基础和结构范式。神经网络通过多层复合函数的堆叠来实现对输入数据到输出数据的深度特征抽象提取，张量为数据流动的血细胞、复合函数是数学基础的骨架、多头注意力构成脑的神经，三者通过“Tensor高阶张量数据元支撑+Transformer多头注意力多层并行映射+梯度反向传播复合函数运算”，融合为三位一体框架体系。 张量是深度学习中的输入数据（如图像编码、文本向量编码）以张量形式流入神经网络， 每一层函数的输入与输出均为张量；在Transformer中每个Decoder层即是一个复合函数单元，多头注意力机制（μlti-Head Attention）的‘多头’即‘多重复合函数’，计算本质是高阶多维张量运算，该操作在张量层面实现并行化函数执行单元，复合函数的非线性与多头多样性共同提升模型知识图谱链接概率，进行多路径复合函数拓扑信息整合，最终形成动态组合的上下文语义提取器和多模态感知表示。 深度学习底层基础三要素的Tensor是整个链路的数据载体、多头注意力是处理序列依赖的核心函数模块、复合函数定义整体计算逻辑，从基础数据表示到复杂语义映射的高阶逻辑模型，形成三者内在耦合关系。

简而言之，数据到语义的映射链路的数据流转与函数组合的闭环：

输入数据（文本/图像） → Tensor高阶多维数学工具表示 → 多头注意力的权重矩阵多层次语义关联的Tensor参数建模（计算Query-Key-V） → 复合函数堆叠而成的复杂映射系统自动微分机制（注意力+FFN）  → 迭代优化输出Tensor → 解码生成目标结果

从一阶谓词到多头注意力机制，是向量空间逻辑向张量空间逻辑的更高阶跨越，必然催生更高阶语言、更高效交流、更高级文明！

人类自然语言是形式化语言，和皮亚诺公理体系一样都属于一阶线性逻辑。而高阶张量是高阶逻辑基础，因此基于深度学习架构的AI，可以演算“桌子⊗椅子”这种（我们一阶语言难以理解的）二阶面元逻辑，可以演算“2⊗2⊗2量子自旋复合态”这种三阶体元逻辑，可以演算“能量动量张量⊗黎曼曲率张量⊗度规张量”这种高阶体元逻辑。

究其根本，复合函数多头注意力机制，本质在于"向量⊗向量⊗向量......⊗向量"这样的高阶tensor数元。

3、对偶不变量

那么，"向量⊗向量⊗向量......⊗向量"这样的所谓高阶张量系统。还有缺陷吗？

很遗憾，由函数复合而成的向量⊗向量⊗向量......⊗向量的向量积系统无法解答“全体自然数的无穷和∑1+2+3..........等价于-1/12”类似的问题。我们惯常思维中，正数之和怎么能等于负数呢？整数之和怎么能等于分数呢？发散序列怎么能等于确定值呢？

换一个角度看，全体自然数的无穷和∑1+2+3..........，与黎曼ζ函数在-1点延拓解析等价，因为ζ(-1)＝-1/12 ，所以全体自然数的无穷和∑1+2+3..........= -1/12

如果我们把ζ(-1)＝-1/12 的黎曼函数复域视作张量复合空间，把ζ(-1)与-1/12理解成对偶空间的对偶量，如同波粒二象性（无穷无尽的波等价于收敛的粒子），则恍然大悟：

黎曼zeta函数有，ζ(-1)＝-1/12；把-1看作ii，即ζ(-1) ⊗ 12ii = 1；得到（∑1+2+3..........）⊗ 12ii = 1

如果⊗视为广义的特征乘积（包含内积），则上述等式在内积空间可理解成（∑1+2+3..........）与 12ii  的内积等于1，也就是说（∑1+2+3..........）与 12ii  强正相关（等价）。这类似于波粒二象性解释（对偶空间一面是无穷无尽的波、另一面是收敛的粒子），（∑1+2+3..........）与 12ii 可看作是二阶张量对偶空间的一体两面，一面是无穷无尽的波另一面是收敛的粒子，一面是平移特征元另一面是旋转特征元，一面逆变张量与另一面协变张量，内积为1意味着二阶复合体的强相关的对偶等价（同构的对偶基）关系。

显而易见，黎曼ζ(-1)＝-1/12，只能通过对偶空间波粒二重性解释。而"向量⊗向量⊗向量......⊗向量"这样的向量积表达，未能体现张量特有的对偶结构（协变张量与逆变张量）。

上节我们说过，如果数学有什么放之四海而皆准的大一统表达，那么这个表达系统就是“模”。与群论（模表示论）比较，当前以复合函数（向量积）为基础的深度学习AI模型缺少对于特征属性度量最关键的“对偶”不变量结构！

更进一步看，对偶空间协变张量与逆变张量的复合特征、系统不变量、系统特征属性，这三者之间存在深刻的内在联系。不变量是特征属性的约束条件（比如对称性限制可能的特征值范围、对偶空间和原空间同构）。协变-逆变对偶性提供了不变量描述的完备性，确保物理定律的坐标无关性。系统不变量、系统特征属性、张量的协变-逆变结构，三者关系在广义相对论（时空曲率张量）、量子场论（规范理论）和机器学习（张量网络）中均有广泛应用，体现了数学结构与物理现实的深刻统一。张量理论揭示系统本质特征属性是协变与逆变关系的对偶统一，不变量则是这种统一性的数学结晶。群论与张量分析是桥梁，将抽象的对称性（不变量）、具体属性（特征值）和数学工具（对偶空间）统一为自洽的理论框架。

协变分量 随基底同向变换（变换矩阵为 T 的转置 T^T），逆变分量 随基底反向变换（变换矩阵为 T 的逆 T^{-1}）。在模表示论中，这种变换性质被抽象为模的作用，协变张量对应模的余变（co-module）结构，而逆变张量对应逆变模（contravariant module），两者通过对偶配对结合为标量（如 v^i w_i to {R}），满足“双线性”性质。当协变张量和逆变张量进行复合时，复合特征使得张量能够在不同的坐标系之间以一种协调的方式进行转换，同时又能保持物理规律在不同参考系中的一致性。通过度量张量连接协变与逆变分量的复合不变量构建系统属性的数学描述，对偶空间中的协变和逆变张量的复合特征为寻找和理解系统不变量提供了数学工具，通过张量的变换和组合可以挖掘出系统在变化中保持不变的物理量。系统不变量是指在坐标变换或群作用下的守恒量，如广义相对论中的时空线元、量子力学中的概率幅。

张量的协变-逆变对称性为特征属性提供了数学表达框架，而不变量作为该框架下的特殊产物，体现了系统本质的恒定性。不变量揭示系统守恒性，张量复合特征属性描述系统多维交互关系，二者共同构成系统在变换下的完整特征刻画。协变张量与逆变张量的乘积（如T^i_j = A^i B_j）构成混合张量，其变换满足“正逆变换抵消”，最终结果为不依赖坐标系的标量，即系统不变量，保证张量积的形式不变性（如物理定律表达式不变）。对偶空间中协变/逆变张量的复合体，其缩并结果可生成不变量，体现系统固有特征属性。当复合张量缩并为标量时，退化为系统不变量，系统不变量是系统特征属性中变换不变的特例。

这些不变量通常由张量的标量收缩（如迹或内积）生成，例如协变张量  T_{ij}  与逆变张量  T^{kl}  的乘积  T_{ij}T^{ij}  在坐标变换下保持不变。对偶空间通过基向量的点积关系定义：协变基  矩阵{g}_i  与逆变基  矩阵{g}^j  满足  矩阵{g}_i . 矩阵{g}^j = δ_i^j 。这种结构保证了协变张量（下标）描述几何对象的投影性质（如梯度），而逆变张量（上标）描述线性组合的系数（如速度矢量）。在曲线坐标系中，协变张量的变换矩阵与坐标微分同构，逆变张量则与偏导数同构，二者通过度量张量  g_{ij}  相互转换。协变与逆变张量的复合（如  T_i^j  ）对应物理量的内禀对称性。系统的特征属性（如频谱、本征值）由特征方程  det(A)- λi= 0  定义，其中矩阵  A  可视为二阶张量。特征值的稳定性依赖于张量的协变-逆变结构。在非正交坐标系中，协变分量（垂直投影）与逆变分量（平行投影）需通过对偶基向量转换，才能保证特征值的坐标无关性。

热力学系统的内能，由能量-动量张量缩并得到；

电磁场张量  F_{μν}  的协变分量表示电场强度，逆变分量表示磁场强度，其复合形式  F_{μν}F^{μν}  给出洛伦兹不变量，构成洛伦兹力密度，描述带电粒子受力的特征属性；

相对论中，四维动量p^μ（逆变）与四维坐标x_μ（协变）的缩并p^μ x_μ 是洛伦兹不变量（能量-动量守恒的数学表达）；

 广义相对论， 度规g_μν（协变）、位移dx^μ（逆变） 张量积的缩并g_μν v^μ v^ν，得到时空距离标量间隔ds²，表达时空线元不变量特征；

黎曼几何中，曲率张量R^μ_νρσ 与自身的缩并（里奇张量），其标量曲率R是时空弯曲的不变量特征；经典力学，动量p_i（协变）、速度v^i（逆变） 缩并p_i v^i 动能（标量不变量）；

量子力学中，波函数的相位旋转（逆变作用）与平移（协变作用）通过规范场（如电磁势  A_μ  ）耦合，形成规范不变性；

量子场论， 场算符ψ(x)（协变）、共轭动量π(x)（逆变） 积分∫ψ(x)π(x)d³x 哈密顿量（能量不变量）；

物质（逆变能量-动量 T^{μ ν}）告诉时空如何弯曲（协变曲率 R_{μν}），时空弯曲告诉物质如何运动（测地线方程），系统不变量与特征属性通过协变-逆变张量的对偶舞步，从而在复合特征的舞台上演绎出万物宇宙深层秩序。

一个单细胞黏箘无智能、n个黏箘却能走出迷宫解出东京地铁最优解，这是因为n个黏箘构成了线性时不变系统，线性时不变系统通过它的冲激响应、频率响应等体现出整体系统的固有特征属性。  

在模表示论中，协变张量和逆变张量的对偶性可以通过对偶模（Dual Module）和双线性形式（Bilinear Form）等概念体现。模表示论（特别是结合代数或群代数的表示论）的协变张量（向量）和逆变张量（余向量）形成的对偶空间概念有着核心且自然的推广。其核心思想是将向量空间替换为模（通常是左模或右模），将对偶空间替换为对偶模，并将张量积视为模的张量积。模表示论的协变张量和逆变张量形成的对偶空间，设V是一个模，其对偶空间V^*可以定义模结构，V^*提供了一个与V上的表示相对应的对偶表示。假设我们有一个群G在模M上的作用，即一个群同态ρ: G → Aut_R(M)。那么对偶表示可能是在对偶模M上的作用，即对于每个g∈G，定义ρ(g): M* → M为ρ(g)(f) = f∘ρ(g^{-1})，这里f∈M*，保持对偶性。 模表示论中更一般的张量（如 (p, q) 型张量）通过模的张量积 `⊗_A`（在代数 `A` 上平衡）来构造。Hom 函子更本质的推广， 在范畴论视角下对偶空间的概念被推广为 Hom 函子，对于左 `A`-模 `M` 和 `N`，`Hom_A(M, N)` 表示所有 `A`-模同态（保持 `A`-作用）的集合，它本身是一个 `k`-模；对偶模 `M* = Hom_k(M, k)` 是当 `N = k`（平凡模，具有平凡作用）时的特例；伴随关系 (Tensor-Hom Adjunction)： 这是模论（和表示论）中极其重要的工具，它推广了向量空间中“张量积和对偶空间”之间的自然同构， `Hom_A(M ⊗_k N, P) ≅ Hom_k(M, Hom_A(N, P))`，其中 `M, N, P` 是适当的模（通常 `M` 是右 `A`-模，`N` 是左 `A`-模，`P` 是 `k`-模）。当 `N` 是有限生成投射模时，有更具体的同构：`Hom_A(M, N*) ≅ (M ⊗_A N)*`，这直接体现了对偶空间（`N*`）与张量积（`M ⊗_A N`）的对偶之间的深刻联系。从张量的角度看，V中的元素可以看作是逆变向量（或逆变张量的一种特殊情况），而V^*中的元素则是协变向量，它们之间的这种对偶关系在表示论中通过对偶表示的形式体现出来，并且对偶表示与原表示相互关联。如果V和W是两个模，那么它们的张量积空间V⊗W也可以定义模结构。而协变张量和逆变张量所在的空间可以通过张量积的方式来构造更复杂的张量空间。例如，一个(k, l) -型张量可以看作是由k个协变张量空间和l个逆变张量空间的张量积得到的，这种张量积空间上的表示可以通过对V和W上的表示进行一定的运算得到，这有助于研究群在更复杂的向量空间上的作用。在对偶空间中，通过度规张量可以进行指标的升降操作，将逆变张量和协变张量相互转换。在模表示论中，这种指标升降的操作也具有重要意义，它反映了不同表示之间的同构关系。也就是说，通过指标升降得到的张量所对应的模表示，与原来的模表示在本质上是相同的，只是表达方式不同，这为研究模表示的等价性等问题提供了一种重要的方法。协变张量和逆变张量形成的对偶空间，在坐标变换下，张量的某些性质是保持不变的，这些不变量在模表示论中非常关键。例如，一些张量的收缩、内积等运算结果在不同的坐标系下是不变的，而这些不变量往往与模表示的一些重要性质相关，比如可以用来判断表示的不可约性等，通过研究这些不变量，可以更好地理解群的模表示的结构和性质。在“对偶模”的统一框架下， 群论的不变性，不仅仅是群集合内部的对称性质、也在于群集合外部的对偶性质。波粒二象性的张量诠释，粒子性（局部化）位置算符 x 为逆变张量（频域平移群表示）， 波动性（非局域化）动量算符 p 为协变张量（空域相位旋转群表示），两者通过傅里叶变换（对偶空间映射）关联e^{ipx} 体现群表示的对偶性。系统不变量对应群的不变子空间（如李群的Casimir算子），特征属性对应群的表示理论（如特征标表），而对偶空间的协变-逆变结构则对应李代数与李群的对偶性。例如，闵可夫斯基时空的庞加莱群生成元（动量、角动量）既是系统不变量，又通过协变-逆变张量（如能量-动量张量  T^{μν}  ）表达守恒律。系统守恒律（如能量 E）在坐标变换下保持形式不变，对应协变张量的变换规则。系统动态响应（如本征频率 ω）表现为逆变张量的坐标独立性，系统不变量与特征属性的相互作用表现为混合张量 T_j^i 的特征坍塌（量子系统哈密顿量对角化H|ψ⟩ = E_n|ψ⟩）。诺特定理揭示了对称性与守恒量的对应性，例如平移对称性对应动量守恒，旋转对称性对应角动量守恒。伽罗瓦理论进一步将不变子群与特征子空间关联，表明域扩张中的特征根系（如多项式方程的根）与群结构的正规子群存在反序对应。 黎曼zeta函数的零点分布（特征属性）通过欧拉乘积公式（无穷积）与素数分布（不变量）关联，体现了无穷加（协变）与无穷积（逆变）的对偶性。

系统不变量是系统在运行过程中保持不变的条件或属性，它直接依赖于系统的特征属性。高阶张量可以分解为不同层次的子张量，对应系统的不同层级结构。复杂系统的特征可通过正规子群与子特征空间的张量积分解，这也是高阶张量的对偶模收敛不变性的分解。高阶张量 T^k_l(V) = V^{⊗ k} ⊗ (V^*)^{⊗ l} 可分解为群 G 的直和表示。例如，二阶张量 V ⊗ V^* 对应 {GL}(V) 的伴随表示，其迹 {tr}(A) 是群作用下不变标量。通过伽罗瓦对应，高阶张量系统可分解为正规子群链的张量积： {T} ≈ ⊗_i H_i   (H_i ⊲ G) ，其中 H_i 是群 G 的正规子群，对应特征子空间的不可约表示。例如，黎曼zeta函数零点分布的素数周期性，可视为旋转群作用下特征根的对称性表现。闵可夫斯基时空的线元 ds^2 = g_{μν} dx^μ dx^ν 中，度规 g_{μν} 为二阶协变张量，承载洛伦兹群 {SO}(1,3) 的表示； 其在复数域的推广（如黎曼猜想）要求 zeta(s)=0 的零点分布满足旋转对称性，对应无穷积∏_p (1-p^{-s})^{-1} 的素数阶子群作用。协变张量（如动量）与逆变张量（如位置）的缩并生成守恒量（如角动量 L = r × p）。在模表示论中，这对应诺特定理的推广。对称群 G 的生成元对应守恒量，而伽罗瓦群 {Gal}(K/F) 的子群链则对应特征子空间的层级分解。子特征空间直和分解： {T} ≈ ⊕_i （V_i ），其中 V_i 为不可约表示； 正规子群张量积分解： {T} ≈ ⊗_j（ H_j ），H_j 为素数阶循环群（如黎曼zeta函数中的素数基底）。

既然以张量的协变-逆变对称性为特征分析基础框架的优势如此明显，那么强化深度学习AI，能否自主学习、自我进化、自动升级，将人工智能架构从一阶谓词到多头注意力再到对偶不变量特征空间呢？

深度学习模型架构，如果升级到以张量的协变-逆变对称性为基础的框架，虽然理论上没有不可逾越的障碍，但实际上重构框架投资成本巨大很难做到。 然而，如果在现有人工智能知识图谱基础上蒸馏、提练、改造，然后重构协变-逆变的特征基，则是一条理论上可行的折中路径。

通过知识图谱的结构化语义蒸馏，可在特定领域构建协变-逆变框架的“实验沙箱”。比如优先在生物医药KG或物理仿真场景中验证，此类领域兼具结构化数据与不变性需求的核心特征。参考三维人脸重建中动作单元（AU）引导的参数回归方法，将生物力学约束转化为张量对称性条件。首先对特定领域知识图谱进行几何化增强，再结合图神经网络学习变换规则，最后通过正则化约束确保张量对称性，而非试图从通用知识图谱中直接提炼普适性的协变-逆变基。通过知识图谱（KG）的语义结构作为跳板，渐进式重构协变-逆变特征基，这一路径需领域知识与深度学习的深度融合，可避免从零构建框架的巨大成本。协变-逆变对称性的本质是张量在坐标变换下的代数规则，依赖于基向量变换与张量分量变换的耦合关系，逆变向量分量随基变换反方向缩放，从而构建张量对称性框架，并以矩阵/张量形式存储变换参数（如旋转角度、缩放因子）， 强结构化数据（知识图谱、分子图、时空网格） ，辅以手动构建或通过强化学习从数据中学习变换规则。引入群论知识增强图谱，将李群（如SO(n)、SE(n)）的代数性质作为先验知识注入图谱（例如定义“旋转操作的复合等于群乘法”)，从而使图谱具备表达变换群结构的能力，图谱关系中蒸馏变换矩阵。采用张量网络嵌入方法，将多元关系表示为高阶张量，其指标对应协变/逆变维度（例如，用三阶张量表示“坐标系1→坐标系2”的变换，其中两个指标为协变，一个为逆变，以匹配张量收缩规则)。从普通变换矩阵升级到协变-逆变基向量，确保基向量在变换下满足协变/逆变规律，。构建图谱中足够的“度量关系”（如距离、角度）定义内积运算，对每个逆变基向量e^i，通过对偶空间理论构造其对应的协变基向量e_i，满足内积不变性（e_i .e^j = δ^j_i）。在神经网络训练中，通过正则化项强制特征表示遵循张量变换规则(例如，若输入特征作为逆变向量v，则其经过变换后的输出需满足v' = T . v，而对应的协变梯度需满足∇ v' = T^{-T}. ∇ v，通过损失函数约束这种对称性)。现有等变神经网络（如3D等变卷积）通过群论实现部分对称性，可将其训练好的变换矩阵（如SO(3)群的不可约表示）作为“额外知识”蒸馏到知识图谱中，再通过图谱的语义关联扩展对称性应用场景（例如，将图像旋转的等变变换迁移到分子旋转的场景中，利用图谱中的“旋转”语义节点共享变换规则）。通过蒸馏和特征基改造实现协变-逆变框架的迁移，本质上是将传统AI的统计学习范式升级为几何学习范式。尽管需要解决跨模态对齐、动态度规学习等难题，但结合知识蒸馏、流形学习和自动化压缩技术，可显著降低重构成本。这一路径的突破点在于，将对称性约束转化为可微的优化目标，而非彻底重构底层架构，因此具有较大可行性。