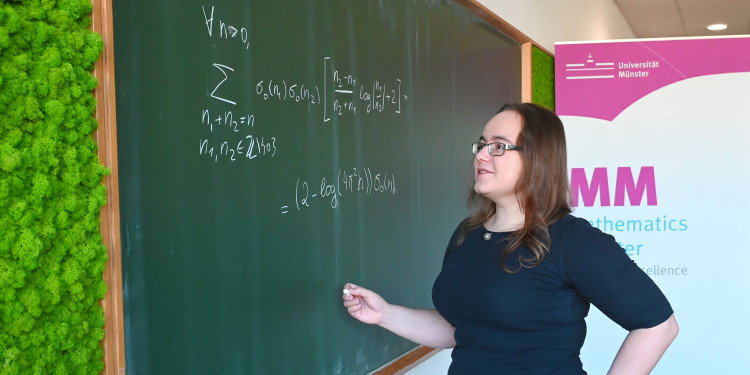弦理论研究的新难题

诸平

Ksenia Fedosova presents an example of the equations from the work published in PNAS. © Uni MS - Victoria Liesche

据德国明斯特大学（University of Münster / Westfälische Wilhelms-Universität Münster, WWU）网站2024年11月15日报道，弦理论研究遇到了新难题（A new puzzle piece for string theory research）。来自明斯特大学卓越数学集群（Cluster of Excellence Mathematics Münster）的科学家证明了物理学的猜想。

弦理论（String theory）旨在解释宇宙中所有的基本力和粒子——从本质上讲，就是世界是如何在最小尺度上运行的。虽然还没有经过实验验证，但弦理论的研究已经在数学和理论物理领域取得了重大进展。

克塞尼亚·费多索娃博士（Dr. Ksenia Fedosova）是明斯特大学数学卓越集群（Mathematics Münster Cluster of Excellence at the University of Münster）的研究员，他与两位合著者一起，为这个谜题增加了一个新的部分：他们证明了一个与物理学家为某些方程提出的所谓的4-引力子散射（4-graviton scattering）有关的猜想。相关研究结果于2024年10月25日已经在《美国国家科学院院刊》{Proceedings of the National Academy of Sciences (PNAS)}网站发表——Ksenia Fedosova, Kim Klinger-Logan, Danylo Radchenko. Convolution identities for divisor sums and modular forms. Proceedings of the National Academy of Sciences (PNAS), 2024, 121(44): e2322320121.  DOI: 10.1073/pnas.2322320121. Epub 2024 October 25. https://doi.org/10.1073/pnas.2322320121

三名作者对论文的贡献是相等的。Ksenia Fedosova来自德国明斯特大学数学研究所（Mathematical Institute, University of Münster, Münster, Germany）；Kim Klinger-Logan来自美国堪萨斯州立大学数学系（Department of Mathematics, Kansas State University, Manhattan, KS, USA）; Danylo Radchenko来自法国里尔大学数学系（Mathematical Department, University of Lille, Villeneuve d'Ascq Cedex, France）。

引力子是一种假想的产生引力的粒子。Ksenia Fedosova解释说：“4-引力子散射可以被认为是两个引力子在空间中自由移动，直到它们在一个‘黑匣子’（’black box’）中相互作用，然后作为两个引力子出现。”Ksenia Fedosova为她的工作提供了物理背景。“我们的目标是确定这个黑匣子里发生事情的概率。”这个散射概率是由一个函数来描述的，这个函数依赖于所有4个引力子的信息。“虽然这个函数的确切形式尚不清楚，但只要过程中涉及的能量相对较低，我们就可以对黑箱内特定类型的相互作用近似于这种散射振幅。”

为了计算这个近似值，还必须考虑它对另一个变量的依赖，即所谓的弦耦合常数（string coupling constant），它描述了弦之间相互作用的强度。“在我们的研究设置中，它的定义域连接了弦理论（string theory）和数论（number theory），”Ksenia Fedosova解释说。弦耦合常数由一个环面形状表示，或者在拓扑上是一个圆环——在这种情况下，它用于紧化不可见的维度。对于数论学家来说，弦耦合常数，或环面（torus），由一个众所周知的模表面上的一个点来表示。后者是一种具有两个圆锥和一个尖点奇点的二维曲面，用于数学和物理中分析特定的数字模式和几何结构。

这就是在模曲面上定义的函数在弦理论中出现的方式。Ksenia Fedosova， Kim Klinger-Logan和Danylo Radchenko研究了这些必须满足某些偏微分方程的函数，并找到了出现在4-引力子散射中的一些函数的正确齐次部分。齐次部分在数学中经常被用来理解函数的基本结构或行为。

“为了简化这个过程，我们在模块化表面的‘未折叠’版本上求解偏微分方程，然后研究是否有可能将解‘折叠’回来，”数学家解释了他们的方法。为此，Ksenia Fedosova和她的合作者需要计算涉及所谓的除数函数的无穷和。这些和的第一个例子是由物理学家发现的，根据数值评估，人们推测它们是消失的。研究小组还发现了更多这样的例子。“然而，有趣的是，其他总和并不一定像物理学家预期的那样消失。我们的结果表明，对于开始的偏微分方程，应该有一个比物理学家目前考虑的更好的选择。”

本研究得到了美国国家科学基金会数学和物理科学理事会{DMS-2001909/NSF | Directorate for Mathematical and Physical Sciences (MPS) and DMS-230230/NSF | Directorate for Mathematical and Physical Sciences (MPS)}、德国科学基金会{Germany's Excellence Strategy EXC 2044-390685587/Deutsche Forschungsgemeinschaft (DFG)}以及欧洲研究理事会{01078782/EC | European Research Council (ERC)}的资助。

上述介绍，仅供参考。欲了解更多信息，敬请注意浏览原文或者相关报道。

Significance

Our research proves a conjecture from string theory asserting the vanishing of a specific convolution sum arising in the 4-graviton scattering amplitude in 10-dimensional type IIB string theory. The conjecture emerges from the Fourier expansion of solutions to a differential equation linked to the low-energy expansion of the scattering amplitude. Our work rigorously establishes this conjecture, showing the expected vanishing of the homogeneous solution. Moreover, our findings reveal a large family of convolution sums of a similar form that yield Fourier coefficients of modular forms.

Abstract

We consider certain convolution sums that are the subject of a conjecture by Chester, Green, Pufu, Wang, and Wen in string theory. We prove a generalized form of their conjecture, explicitly evaluating absolutely convergent sums

where φ(n₁, n₂) is a Laurent polynomial with logarithms. Contrary to original expectations, such convolution sums, suitably extended to n₁∈{0, n}, do not vanish, but instead, they carry number theoretic meaning in the form of Fourier coefficients of holomorphic cusp forms.