博文
高分子熔体的剪切弛豫
 精选
精选
|||
高分子熔体的剪切弛豫
侯吉旋
根据维基百科的解释,高分子就是由许多重复结构单元组成的大分子。我们日常使用的塑料袋就是由高分子组成的。据统计,仅台湾地区一年就要生产超过百万顿的塑料薄膜。一般生产塑料薄膜的方式就是吹制。要了解吹制过程,就必须了解高分子的流变性质。
一个简单的例子就是我们孩童时代常玩的橡皮泥(silly putty)。将一个橡皮泥捏的小球扔到地上,它会像乒乓球一样反弹回来,这说明在短时间内它具有弹性。如果观察橡皮泥长时间(例如超过1秒)的行为,就会发现它和黏的糖浆一样会流动。
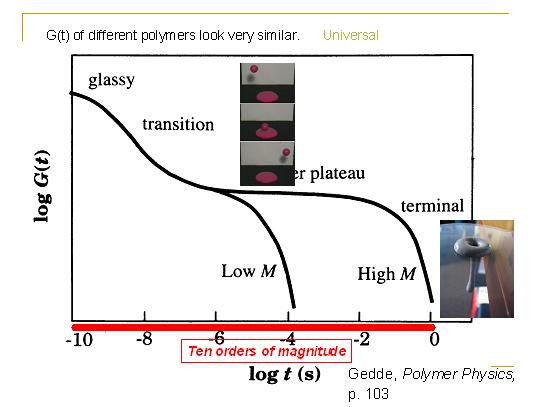
作为物理学家,如何研究一个体系呢?一般都是在样品上施加一个改变,然后测量样品的响应。要研究高分子熔体的流变性质,我们一般在样品上突然加上一个水平的剪切力,然后测量其应力。我们定义剪切弛豫模量G(t)就是在剪切很小的时候应力的大小除以剪切的大小。我们来看看应力随时间变化的几个例子:对于一般固体,服从胡克定律,应力的大小正比于剪切的大小,当我们施加剪切后,应力就不变化;对于一般液体,它不能提供应力,施加剪切后应力还是0;对于高分子液体,情形就不一样了,它首先是和固体一样有应力,然而随时间变化应力会降低到0,长时间后就和液体一样了;橡胶的应力也是会降低,但不降低到0,而是会达到一个平台。
对于不同种类的线性高分子,在应力弛豫方面却表现出普适性,实验测量出它们的剪切弛豫模量G(t)的形状都非常相似。将G(t)用对数对数作图,会看到在短时间内是以幂指数下降的,然后遇到一个平台,之后到了终结时间以后就以指数形式下降。如果熔体中的高分子链比较短,平台持续的时间久比较短;如果熔体中的高分子链比较长,平台持续的长度就比较长,可以达到秒的数量级,整个弛豫过程可以跨域10个数量级的时间范围。由于有弹性平台的存在,所以橡皮泥短时间内还是弹性的,但是超过终结时间以后,平台就结束了,橡皮泥就像粘性的流体一样。
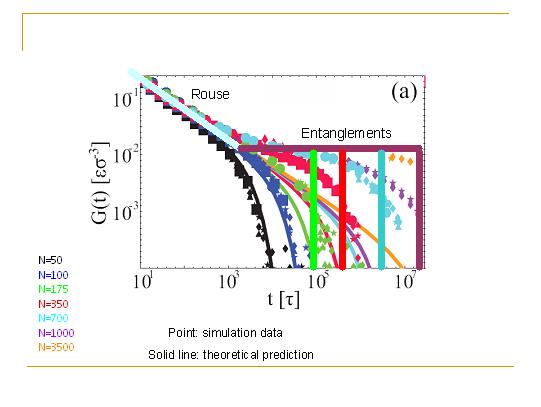
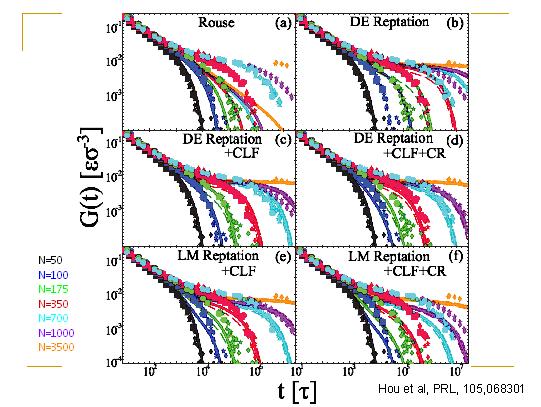
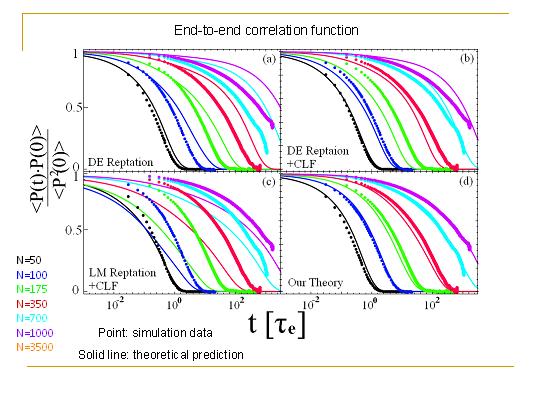
由于普适性,所以我们不必去模拟非常复杂的高分子,而是模拟简单的珠子-弹簧高分子模型(Kremer-Grest model)即可。我们模拟了珠子-弹簧高分子熔体,并得到了应力弛豫模量的一系列数据。图中不同颜色代表不同长度的高分子链,从每条链包含50到3500个珠子不等。我们的模拟数据重复了实验的观测结果。然而如何理解为什么G(t)会有这样的形状,我们就必须从理论入手。
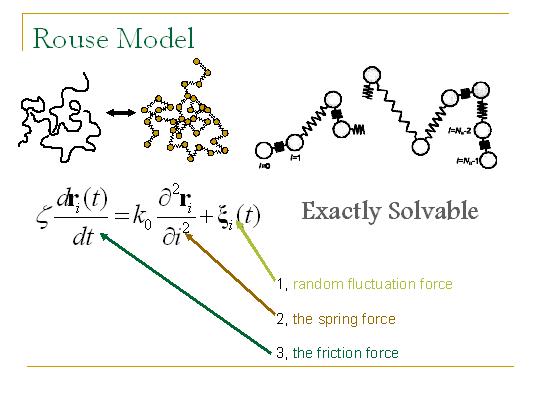
第一个理论模型叫做Rouse模型,是由Rouse在上世纪50年代提出来的。由于在大尺度上任何高分子都可以通过粗粒近似简化为珠子-弹簧模型,所以Rouse研究单个珠子-弹簧高分子链。每个珠子的运动都可以用方程表示,只受三种力:1、环境随机碰撞产生的随机力;2、弹簧施加的力;3、液体的粘滞力。由于Rouse模型非常简单,这个模型精确可解。
我们将Rouse模型寓言的G(t)与我们的模拟数据进行比较,发现Rouse模型只有在非常短的时间内成立,或者对非常短的高分子链成立。研究Rouse模型可以让我们理解短时间内的幂指数下降,不过Rouse模型却不能给出任何的平台。那究竟Rouse模型少考虑了什么呢?
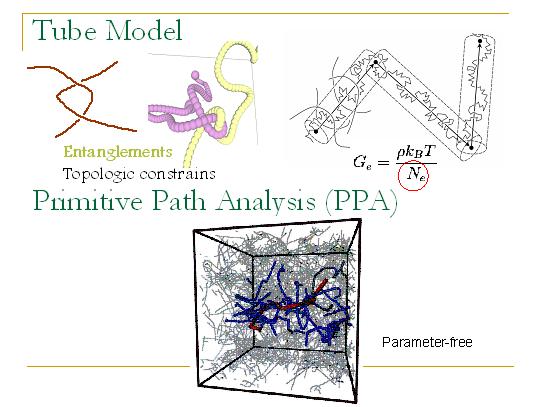
纠缠,Rouse模型没有考虑的重要因素。由于高分子链之间不能相互穿越,所以这种不可穿越性就造成了拓扑的限制,叫做纠缠。数学上处理纠缠是非常困难的,但是Edwards将相邻高分子链给某条链的限制类比为包含该链的一条管道(Tube),我们要研究的高分子链就限制在这条管道之中,这就是管道模型。管道模型就寓言了一个弹性平台,这个平台模量的大小等于Ge=rkBT/Ne. 其中Ne表示两个相邻纠缠点之间的单体的数量。在最初的管道理论中,Ne只是一个可调参数,用来拟合平台的高度。但是有了原始链分析法(Primitive Path Analysis (PPA))之后Ne就不再是拟合参数了,而是可以直接测量的物理量。原始链分析法在下文会提到,在此暂且不表。因此,管道模型给出了一个平台,而PPA给出了这个平台的高度。
Rouse模型给出了最初G(t)下降的幂指数,纠缠给出了平台,但是还有一点没有说明的是,平台不是无限长的,会在某个终结时间结束。因此我们还需要一个理论来寓言纠缠的寿命和平台的最终下降时间。
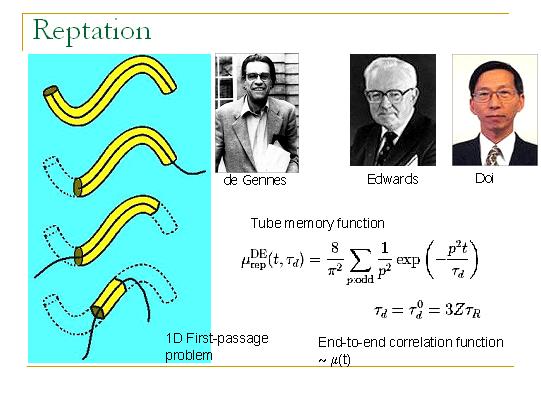
de Gennes给出了一种弛豫机制,叫做爬行(Reptation)。高分子链只能局限在管道中并沿着管道运动,当高分子链从管道的某一个端口处爬出的时候,另一个端口处的老的管道就消失了。每当链的一个端点运动到管道的某一点时,原始的管道就缩短到这一点,这就是一个一维的首达时间问题(1D First-passage Problem)。所以最开始形成的管道在逐渐的缩短,管道的记忆就在逐渐的丢失。这个过程的数学形式由Doi和Edwards (DE)给出,它们给出了爬行过程的管道记忆函数(Tube memory function)。由于高分子链爬出管道的部分的取向是随机的,所以顶对顶的关联函数(End-to-end correlation function)是正比于管道记忆函数的。
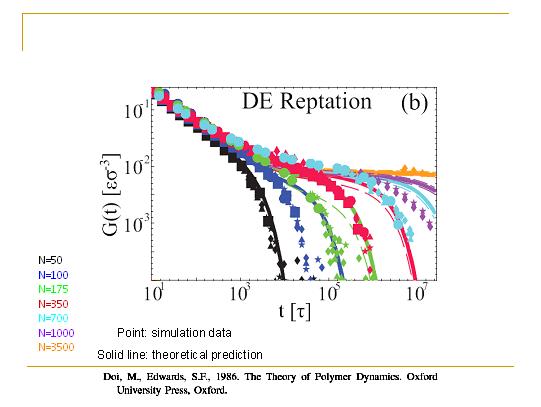
如果考虑了爬行过程,我们来看看现在理论和模拟符合得如何吧。在图中如果不管颜色的话,还以为理论和模拟数据符合得很好,但是仔细一看理论高估了最终的下降时间。这说明只考虑单纯的爬行过程还不够,还有其他机制在加速这个弛豫过程。
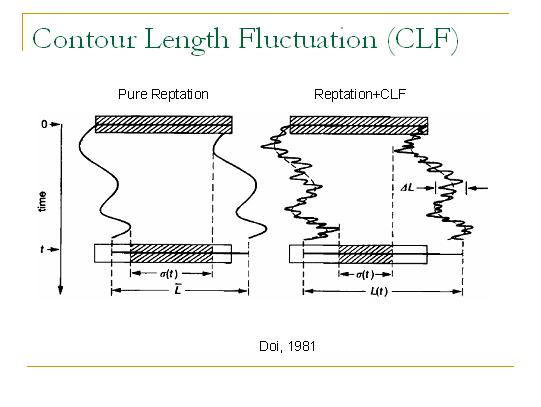
这个过程叫做长度涨落(Contour Length Fluctuation (CLF)),最早由Doi提出来。之前提到,管道弛豫过程就是一个一维首达时间问题。单纯的爬行过程就是一个一定长度的首达时间问题,而有了长度涨落机制后,这就变成了有涨落长度的首达时间问题。有长度涨落之后管道就会更快地丢失记忆。
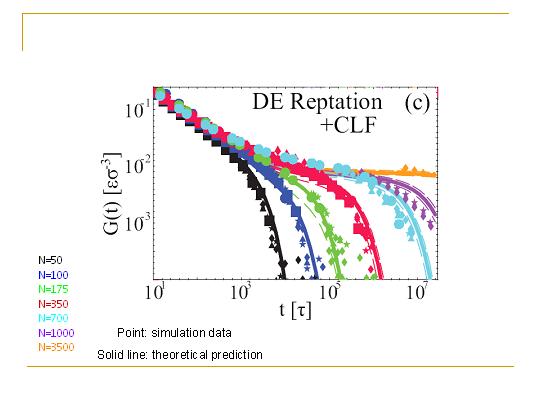
考虑了长度涨落以后,理论和模拟数据吻合得好多了,只有在长链的时候还高估了最终弛豫时间。高估了最终弛豫时间。
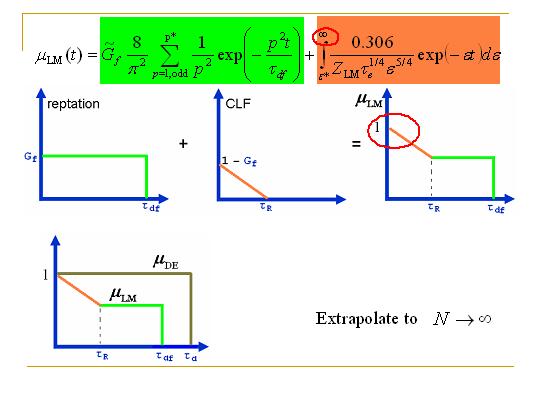
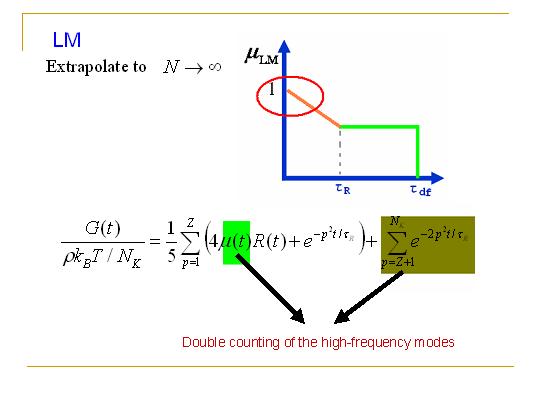
在2002年,Likhtman和McLeish (LM)给出了线性高分子的新的理论。由于管道弛豫是一个有长度涨落的一维首达时间问题,因此LM研究了一维Rouse链的首达时间问题。这个问题数学上求解及其之困难,因此LM运用计算机随机方法模拟解决了这个问题。这就用一种自洽的办法并和了爬行和长度涨落两种机制。最后LM还把一维的Rouse链的珠子数量外推到无穷大用以消除不确定性。
LM给出了他们的管道记忆函数。这个管道记忆函数看起来虽然非常复杂,但是每一项的物理意义是非常清楚的。绿色的部分代表了爬行过程,它最终在tdf时刻衰减。而橘色部分代表了长度涨落过程,它在Rouse时间(tR)结束。由于考虑长度涨落,LM给出的管道记忆函数比DE给出的衰减得快。
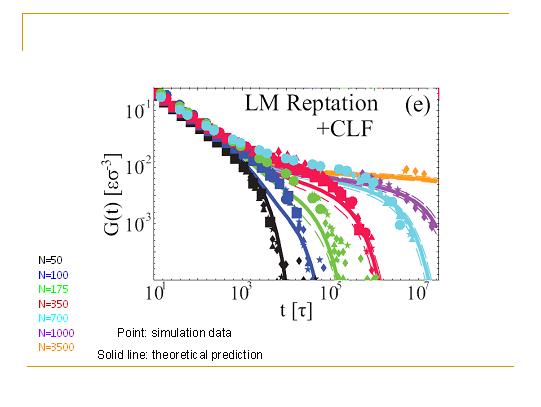
可以看到LM给出的理论和模拟数据在定性上符合得也是很好的,但是在定量上还是有一定问题。那是否还存在其他机制呢?
这个机制就叫做限制脱落(Constraint Release (CR)),最早由de Gennes在提出爬行机制的时候就一并提出来了。由于管道是由周围的链构成的,而其他链也会运动,因此当一个构成管道的链移走的时候,这个限制就消失了。
限制脱落时一个多体问题,处理起来非常困难,但是des Cloizeaux在1988年提出来一个双重爬行近似(Double Reptation Approximation),可以很简单地对限制脱落做近似处理。一个纠缠点是由两条链铰接而成,因此一个纠缠点存在的几率是等于单条链存在几率的平方。而G(t)正比于单个纠缠点存在的几率,所以双重爬行近似告诉我们G(t)正比于管道记忆函数的平方。
当考虑了爬行、长度涨落、限制脱落等机制以后,理论和模拟数据在长链部分吻合得非常好,但是对短链来说,理论低估了G(t)。
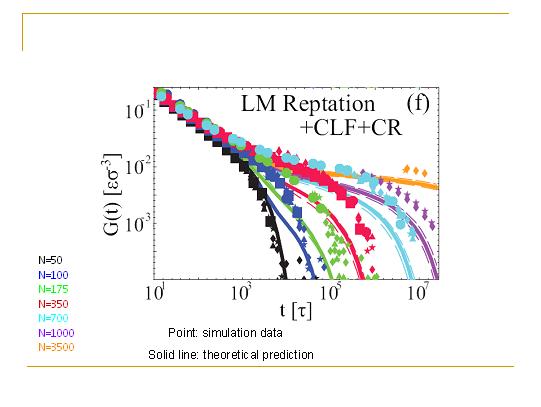
而当把LM的理论和双重爬行近似相结合的时候,我们发现理论在数值上强烈地低估了G(t)。
到此,我们展示了一系列理论和数据的对比图片,但是我们还没有说这些理论的图线是如何画出来的。
我们是根据LM给出的G(t)的公式画出理论图线的。LM的公式有机地结合了(1)早期的Rouse弛豫、(2)管道中张力平衡过程、(3)爬行机制、(4)长度涨落和(5)限制脱落。
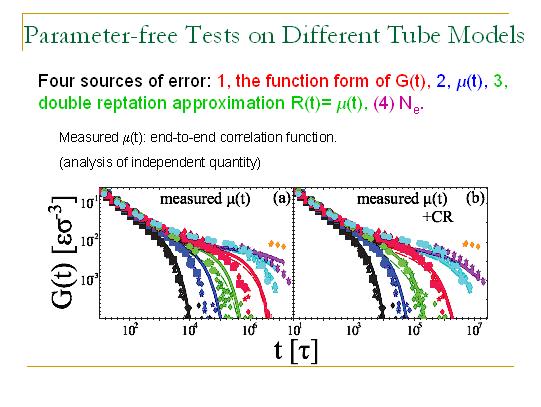
理论和数据符合得不好可能是以下四个原因造成的:(1) LM给的G(t)的公式不对,(2) LM给出的管道记忆函数不对,(3) 双重爬行近似不对,(4) PPA给出的Ne的值不对。为了做出一个非常准确的判断,我们在计算机模拟中测量了管道记忆函数,就是顶对顶的关联函数,这是和G(t)在分析上是不关联的量。如果我们使用模拟测量到的管道记忆函数代替LM给出的管道记忆函数重新画G(t)曲线,我们发现结果和G(t)的模拟数据吻合得相当好,所以我们可以认定是LM给出的管道记忆函数有问题。
我们下一步的目标就是(1)矫正LM给出的管道记忆函数,(2)将我们的理论连接到PPA。
由于在LM的G(t)的公式里已经包含了高频的Rouse模,而在m(t)中又应为外推到N至无穷大而包含了高频模,所以LM的理论重复地计算了高频模量,以至于低估了G(t).
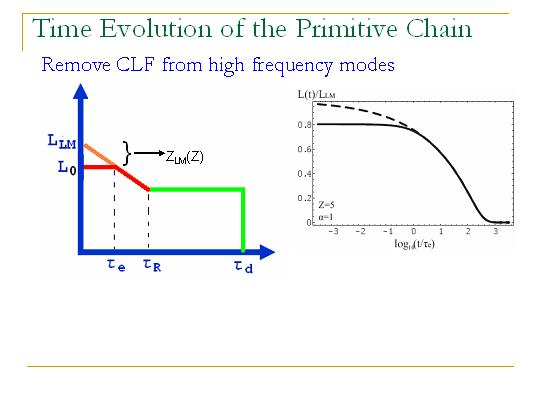
我们需要做的就是在LM的管道记忆函数中移除高频模量,使得管道记忆函数不是从t=0时刻就开始衰减,而是从te以后才开始衰减。修正了LM理论以后,我们得到的理论和数据符合得很好,且看下面几幅图。
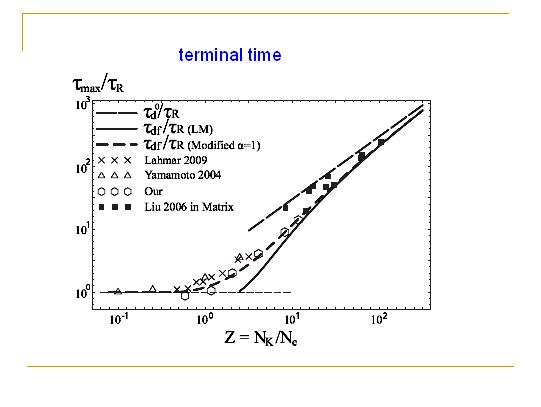
关于最终衰减时间,对于短链来说应该等于Rouse模型所预言的Rouse时间,而对于非常长的高分子链应该等于纯爬行理论所预言的解纠缠时间。对于中间长度的高分子链,LM低估了最终衰减时间,我们的理论却和模拟数据符合得相当好,并且在短链极限退化为Rouse时间,在长链极限和纯爬行理论所预言的时间一致。
关于顶对顶的关联函数以及剪切弛豫模量,相比较其他理论而言,我们的理论也可以与数据符合得非常完美。说明我们的修正是非常合理的。
对于粘度,相对于实验数据来说,LM低估了短链系统的粘度,而我们的理论与实验符合得非常好。
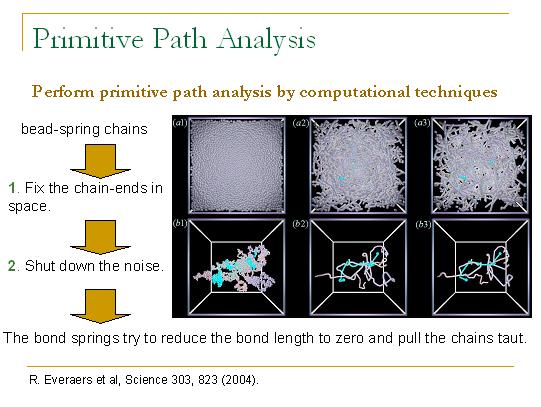
原始链分析法是由Everaers等人在2004年提出来的。对于珠子-弹簧模型来说,在计算机模拟中实施原始链分析法首先是将链端在空间中固定住,然后把随机涨落力给消除掉,最后由于弹簧的作用会让链缩紧并让系统处于能量的基态。
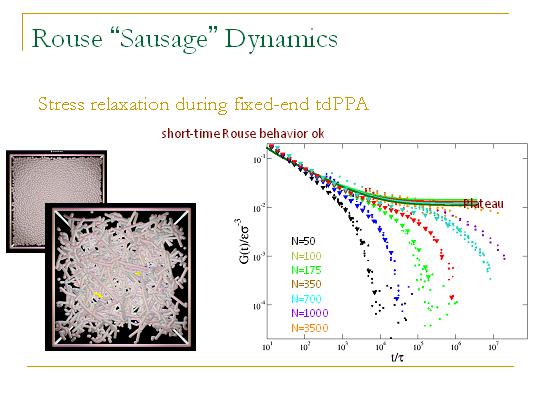
在PPA的过程中,如果我们测量这个过程中G(t)的变化,我们会发现PPA给出的G(t)在短时间内和Rouse模型给出的结果一致,而在te之后能够给出一个正确的平台。因此我们可以说PPA不是一个电脑游戏,而是能够给出正确的短时间弛豫过程和纠缠信息的方法。
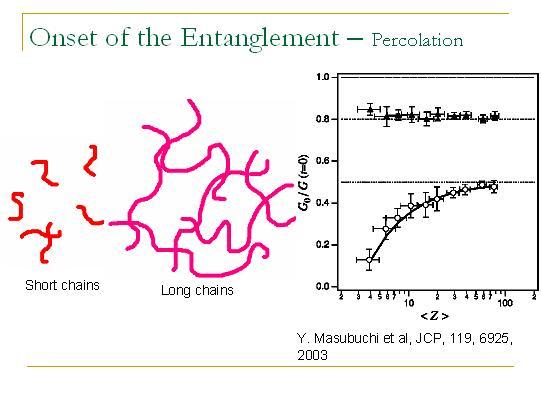
最后,我们预言了在线性高分子系统中的渗流转变。对于短链来说,它们不能形成一个网络,而对于长链,则可以形成一个网络,这个就对应于渗流转变。当然,这个网络最终会通过管道动力学而衰减。一个证据就是Masubuchi通过模拟发现长链可以有平台模量,而当链长小于一定长度后,就不再具有平台模量。
https://wap.sciencenet.cn/blog-84519-596628.html
上一篇:为何桥面下方的河水不易结冰?
下一篇:吴有训-王竹溪气体平衡问题