6.2第6章降水统计力学—气象统计学私探（27）

张学文，2020 10 07  基于1985-2006年的文稿，

下面是第6章第1节的第2部分（2）

 （2）进一步的雨深面积关系 

  有了（6．14）式我们可以推论一系列特定含义的雨深与面积的关系．

  （2.1）降水超过某一限度者所笼罩的面积

现在假设在某区发生了一次降永过程，其平均雨深达到了5 0毫米。现在问降水超过I 5 0毫米者占了总面积的百分比是多少？

显然为求出答案只要对面积函数f_a(x)的雨量x从150积分到充分大(数学上做无穷大处理)就可以了。如以F代表这个比值，依（6．14）有

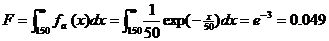
即降水大于150mm者占了总雨区面积的百分之4.9。

从上例看出降水超过x者占的总相对面积F为

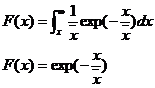   （6.15）

这个式子对于求算达到一定暴雨量的面积是多少有用的。

如果在做上述积分时把下限x取为零，则得出F=1．这是什么含义?这显然是说降水大于零的地区占了总面积的全部(100％)，这是理所当然的。这个计算说明我们得出的物理模型在特定场合下的物理含义也是妥切的。

 如令a表示降水超过x者占的绝对面积，依(6·15)我们可以得出

     （6.16）

可见只要知道总雨区面积A，平均雨深，我们可以求出雨量大于任—给定值x者占了多大实际面积。

（2.2）暴雨部分的总降水水体体积

在防洪中人们常关心暴雨部分总共形成了多少降水．这实际上也不难从(6.14)式求出。   

我们令降水为x→x+Δx者造成的隆水总量为Δv(x)_则应当有

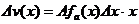
式中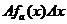为降水在x→x+Δx者占的相对面积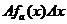为其绝对面积。它与x相乘为其水体总量。把上式变成微分再从x积分到无穷大即得降水超过x者形成的总降水水体的体积v(x)即

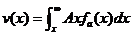
还利用(6·14)式我们积分得

     (6.17)

利用(6.16)式还可以写成

       (6.18)

这两个式子都是最可机分布下降水量超过x者所形成的总降水水体的体积的理论公式。

    如=50mm，A=50×10⁴Km²即有一场总面积为5 0万平方公里的平均雨深为50毫米的降水过程，那么降水大干1 5 0毫米的那些地区(不一定是一块连通的雨区)总共降了v立方米的水。此处v应为

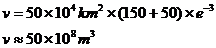
即有5 0亿立方米的降水。这对估算流域暴雨总水量显然十分重要而且方便。

在x=0时的(2.I 8)式表示降水大于零区域的总降水，这时v的含义变成了V，a的含义变A而有

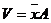
这与(6.1)式一致。即(6.18)式可退化为（6.1）式。

如将（6．18）式写成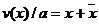,我们还可以把v(x)/a叫做降水超过x的部分的平均雨深。如以示它，则有

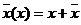      （6.19）

这个式子表明降水超过x的部分的平均雨深是总平均雨深与x的合计值。用天气分析上的语言说．上式表明在最可机分布下，地图上雨量等值线为x所包括的地区的平均雨深为总平均雨深x加上这条等值线上的雨量值。

实际情况是否如此?我们欢迎读者试一试．在x=0时上式退化为=。这显然是合理的。

（2.3）平均雨深与面积的关系

水文上人们经常统计的是平均雨深和相应的面积。我们也容易把关系移到这些变量上来。实际对（6.17）和（6.18）分别取对数再联立得

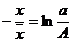
将上式再与(6.19)式联立我们得

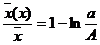  (6.20)

这里的还是雨区的平均雨深，为雨量大于x的部分的平均雨深．也可写成（0）它是x>O时的。

上式表示了平均雨深与其所占面积的对数有线性关系。

平均雨深和它占确的面积这两个项目是水文工作者经常统计的项目：现在又有了根据最可机理论得出的这两者的理论关系。这就为验证这一理论提供了条件。这里我们利用在文献[6.1]中提供的数据作了这种验证。在公式中对每次降水而言和A是常数。所以--平均雨深与其占的面积a的对数成线性关系。据此我们用实际资科来检验它们是否为直线关系。文献[6.2]中曾给有美国大暴雨过程中平均雨深与其笼罩酉积的数据。我们用其平均雨深和面积的对数作为两个变量，计算它们的线性相关系数，很显然如果(6.20)式成立这个相关系数应当等于1。我们针对不同时段的上述两个变量计算出来的实际相关系数值现列于表（6·l）中．

表（6·l）    美国最大实测暴雨的雨区面积的对数

与其平均雨深的相关关系（不同历时）

从表中看出这两者的相关系数很接近于-1。说明面积的对数与平均雨深确实很近于直线关系。这说明了我们推出的公式(6.20)是正确的。它是对最可机降水分布思路的有力支持。另外，在世界气象组织提供的暴雨时面深分析手册中[2]有l953年5月l6-18日美国暴雨资科。我们对它做的计算也表明相关系数很高。这些原始资料的整理人事先都不知道我们的理论结果，但他们整理得出的结果竟与这一理论如此吻合，显然不能看成是—种巧合。这说明这个思路是抓住了客观事物中的较核心的部分。

  为进一步验证上述理论，邓子风、周正立选了新疆降水三个例子来验证。为此，首先从利用降水分布式求出降水介于x₁→x₂之间者占了多大的相对面积F。这只要积分原式即可得出

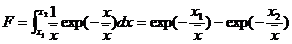
我们取平均降水量为3-15，x₁→x₂的间隔为10mm,而得理论分布（表6.2）

表（6.2） 不同雨量占的面积的理论分布

续前表

下面是他们从新疆实例计算的结果，其中1984年的例子的平均降水量=12，1978年的=3.4。

表6.3 两个实际的降水面积分布

对比这两个表中数字可看出它们的大趋势是完全一致的。但在某个档次上的百分比可有不高于7％的误差。我们尊重原降水量图的分析和它并不完全符合新疆的情况下得到这种结果。对此我们是十分满意的。有这个误差并且说它出于分析与采样是完全可以的。如果理论与实际完全一致，倒是值得怀疑。另一例子因为平均值一致故未列出，但它也说明上述理论的正确。

（2.4）等雨量线的分布

为了分析每次降永过程在各地的雨量分布，气象水文人员常在地理底图上分析等雨量线(雨量的等值线)。分析和见过这种图的人都会发现各次天气过程尽管不同，但造成的雨量等值线的分布形状总有某些共同的特征．例如降水量常常是边缘部分中中心部分大、等雨量线如果按等差级数加大，那么靠进中心部分的等值线总是太密等等。在图中（图略，2006）我们给了一个示意的天气过程雨量图。它大致体现了雨量小的占很大面积，而大降水的仅占很小面积的一般特征。图中右侧的降水分布尽管不能说它那里错。但任何一个气象水文人员都从没有见过如此古怪的分布。这说明气象水文人员虽然没有什么理论概念，但他对降水分布是有明确认识的。他知道那些合理，那些是根本不可能出现的。

有了降水与笼罩面积的理论关系以后，只要用最简单的假设就可以求得等雨量线应当是如何分布的了。这里假设等雨量线簇是同心园(如是一簇同心椭园也可)。这时如以r和R分别表示降水为x和总雨量区的园形半径，那么依(6.16)式和半径与园面积的关系可以有

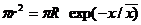
以k 表示r与R的比值我们进而得出

k实际的含义是雨区等值线(现征是同心园)的相对半径。我们对分别依等差级数取为0.5，l.0，l.5，2．0，2．5…．或依等比级数取值为0.4，0.8，1.6，3.2…那么从上式中可求得相对半径的分布了。这种相对半径与相对降水的关系我们在图6·2中给出．图的上半部是依等比级数作的，下半部则为等差级数关系。

图6.2 等雨量线的理论分布

（上半部分等值线是安等比级数挑选，下部按等差级数挑选）

如果回忆一下我们分析过的雨量图上等雨量线的疏密关系不难看出这个图是与一般经验完全一致的。当用等差级数表示降水时，在大降水区常常是等值线密得画不开。而改用等比级数就均匀多了。这也是促使我们建议天气学工作者和水文工作者分析天气过程形成的降水量时最好等雨量线是依等比级数取值。再者我们有了如上理论关系对于雨量记录稀少地区的等值线分析也会利用这个理论关系把等雨量线分析的更合理一些。

在结束这一节时让我们把这里涉及的假设与物理思路再整理一下。

在这一节我们建立了天气过程中形成的降水的降水量x与其占雨区面的相对大小的一个最可机理论关系。得出的最主要公式是

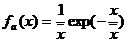   （6.14）

通俗地把f_a(x)看成降水出现于x±0.5范围内者所占的面积与总面积的比值。严格地说应该把f_a(x)称为降水增加单位值时，降水面积的增长量，它的因次是降水量的倒数。它与降水增量相乘才是无因次的面积比值。我们称它为雨深面积函数。

降水所以遵守上述方程是基于如下的假设，即：大气是完全任性地毫无偏爱地把总量为V的水体洒到大地上。在它降落的总面积A上这种完全任性(最无规律)的结果导致有的地方很多，多数地方很少。它们最可能出现(最容易碰上，最易于实现，实现这种结局的机率最高……)的分布就是满足上述定量关系的分布方式。

作为一个学过天气学的人，抛掉天气规律的思想束缚而这么想似乎不应该。但这样做得出的可结果又与天气事实相符的事实也使我高兴，这也促使我沿着这一思路走下去。