11.8 旋转群

   我们知道，代数基本定理【任何复系数一元n次多项式 方程在复数域上至少有一根(n≥1)，由此推出，n次复系数多项式方程在复数域内有且只有n个根（重根按重数计算）】有深刻的内涵。

   比如，如果我们求解1的立方根，会发现实数域只能得到一个根，而复数域能求得三个根（这意味着复数域完备性）：

   形象而言，上面的三个根分别是旋转120度、旋转240度、旋转360度，类似于下面图标：

   也类似于对称分量法：

   更普遍地，一元n次方程的解，所有的根按照1/n距离均匀分布在单位圆周上：

   历史以来对代数方程求解，一直是数学家孜孜不倦的追求。直到十九世纪埃瓦里斯特·伽罗瓦用群论彻底解决了根式求解代数方程的问题，而且由此发展了一整套关于群和域的理论。    

伽罗华（

Evaristr

Galois

）开创群论以后，代数不再以方程为中心，而是以各种代数结构为中心。

   伽罗瓦开创了群论以后，代数不再以方程为中心，而是以各种代数结构为中心。群论开辟了全新的研究领域，以结构研究代替技巧计算。群论在错综复杂的现象中寻求共同的结构，把偏重技巧计算研究的抓瞎碰巧的思维方式，转变为用结构观念研究的有的放矢的思维方式。“无论在什么地方，只要能应用群论，就能从一切纷乱混淆中立刻结晶出简洁与和谐”

   群论是研究对称性问题的数学基础，可直接得到与对称性质有关的结论。

   群论最大的作用，是可以大大简化计算。

   正如本章我们介绍的，无论是量子力学或是相对论空间都包含了旋量。旋量对系统的完备性具有普遍意义，代数基本定理【在复数域内有且只有n个根】 清楚地说明了这一点。因此，在深度学习人工智能中，要确保误差率，必然要研究完备性，当然也将不可避免地遇到旋量。

    如果以‘一组’线性向量来完备地表达‘一个’旋量，以张量扩展之，当然是可以的，但这样会造成系统数据量过于庞大，运算过于繁杂。

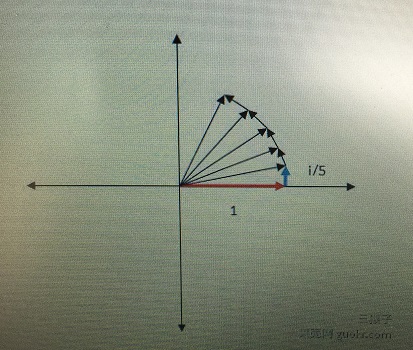
    进一步看， 当我们以首尾相接的一组线性向量来合成旋量时，首尾相接的一组线性向量意味着就是张量积。首尾相接的一组线性向量，相当于向量间n次乘积（即n阶张量）。但是，n阶张量的运算过于繁杂，在有限时间内很可能无法完成足够的训练样本，欠拟合，造成系统难以满足调参需求。深度学习的效果很大程度上取决于参数调节的好坏,那么怎么才能最快最好的调到合适的参数呢? 答案是简化运算。

    解决深度学习张量运算的困窘，必须有一种理论可行的简化运算方式。而旋转群理论正好就是这样的办法。

    下面以转动群SO(2)为例简要说明：

  以exp(ipr)为基底，意味着旋转群与周期函数的等价性，也意味着旋转群可以作傅立叶分析，可以应用卷积定理，从而大大简化运算。

   更进一步看，为什么SO(2)群与exp(ipr)息息相关呢？

   如下：

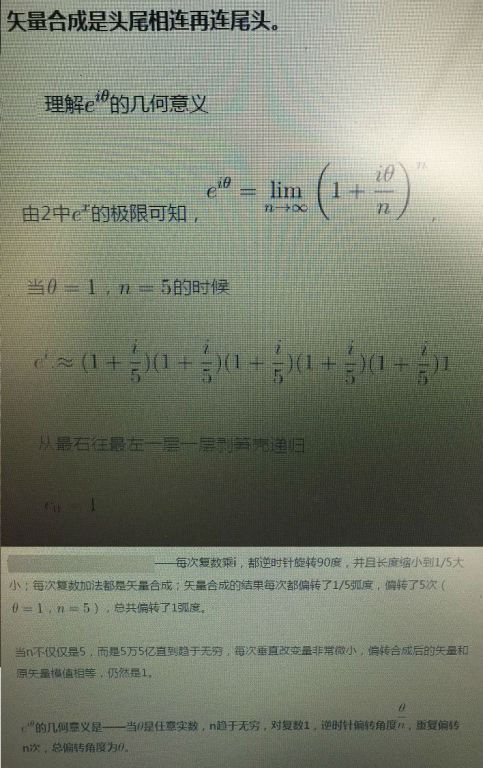
   三维空间粒子自旋是SU(2）群，其无穷小算符分别对应于三个自旋角动量算符。SO(3）群的无穷小算符对应的是轨道角动量的算符。（注：SU(2）群和SO(3）群是等价的。SO(3）群刻画了三维欧式空间的所有旋转，SO(2）群刻画了二维欧式空间的旋转）

（插一句，上面这个式子可以推演出指数映射与线性时不变系统的深刻内在关系，如下：）