博文
关于不完备性定理和不确定性原理的探讨(五)(6)
|
5.6 大众情人
随便翻开一本人工智能教科书,核心内容都会介绍如何识别特征、提取特征、分析特征。那么请问,应用最广泛的特征基长什么样子呢?
这就是exp(ipr) 特征基
上一节的例子可以看出平面波exp(ipr)是自然科学的大众情人,让我们来看看大众情人到底有多么的“大众化”。 下面是关于exp(ipr)广泛性的一个著名定理。
【定律】exp(ipr)是所有线性时不变系统的共同本征函数(特征基)系。
【证明:
设L是任意线性时不变系统,v是输入,w是输出
即 w=Lv
则 w(x)=h(x)*v(x) ,即w可以表达成h和v的卷积
上式傅里叶变换记为:
W(p)=H(p)V(p)
如果输入exp(ipx) ,即 v(x)= exp(ipx)
则由:
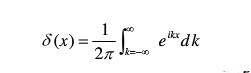
得到:v(x)的傅里叶变换V(p)等于脉冲函数δ(x-p) [注:为方便表述,exp(ipx) 省略了常数项2π ]
则输出:W(p)=H(p)δ(x-p)=H(x)δ(x-p) [注:此处H(x)是个常数]
再通过傅里叶反变换,把上式从频域返回到时域,得到:
w(x)=H(x) exp(ipx)
此处H(x)是个常数,记为c,则:
w(x)= c exp(ipx)
即:输入exp(ipx) ,通过L线性时不变系统w=Lv,输出得到 c exp(ipx)
即:L exp(ipx) = c exp(ipx) [注: L作用在exp(ipx) 等于常数c乘exp(ipx) ]
即: exp(ipx) 是任意线性时不变系统L的本征函数
证毕。】
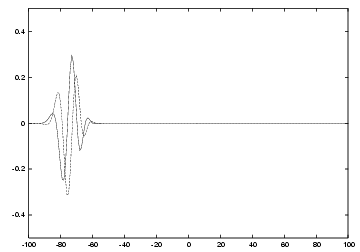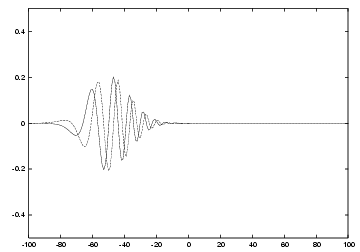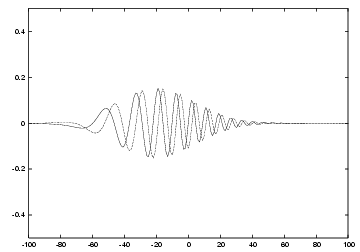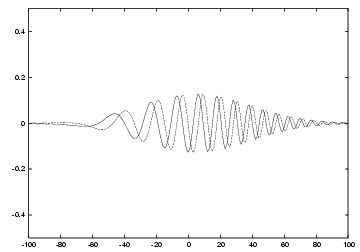
证明过程简洁而深刻,更加深刻的它的意义。任意线性时不变系统共同本征函数的定律告诉我们, exp(ipr)具有放之四海而皆准的意义。
第一,线性系统具有广阔的广泛性。(线性系统的介绍上面提过)
第二,时不变系统具有广阔的广泛性。(时不变最简单的例子是时间变换下的函数性质不变性,比如今天看是这样,明天看还是这样,就是时不变的。另特请注意,时不变的意义不仅仅针对时间变换而言,时不变系统的变量可以是时间、也可以是其它变量,时不变系统具有非常广泛的含义,时不变系统的本质是特征属性不变性。特征属性不变性,在不完备系统中体现为概率不变性。)
下一节将进一步证明,exp(ipr)本征函数的广泛性非常广阔,因为它是一个ℵ 2维度(阿列夫2维度)的空间特征基。 这意味着,exp(ipr)本征函数系空间远远超越希尔伯特空间的ℵ 1维度(阿列夫1维度)、远远超越形式逻辑空间的ℵ 0维度(阿列夫0维度)。
为什么exp(ipr)具有广阔的广泛性,除了上面傅立叶变换理论的严格证明,我们还可以从其它角度来理解。
比如,exp(ipr)是动量算符和坐标算符的共同本征函数系;同时,exp(ipr) 又是动量和位置的内积。这表明对动量和位置而言,exp(ipr)即是基、又是投影,是构成动量和位置线性空间的一切因子。
又比如“卷积”现象。
傅立叶变换理论中有一个著名的定理,两个函数的卷积等于其傅立叶变换的简单乘积。
为什么复杂的卷积能够转换为简洁的乘法运算呢,实质是因为exp(ipr)是所有线性时不变系统的共同本征函数系,因此exp(ipr)可以在线性系统中随意穿越,从逻辑运算括号中渗析而出,从而变成简单乘法。
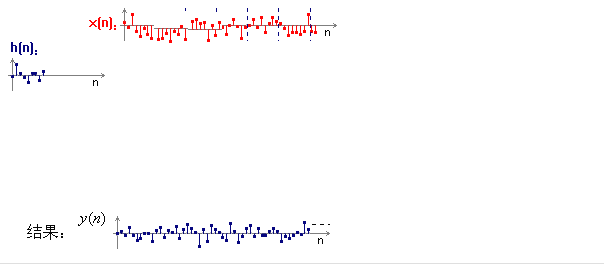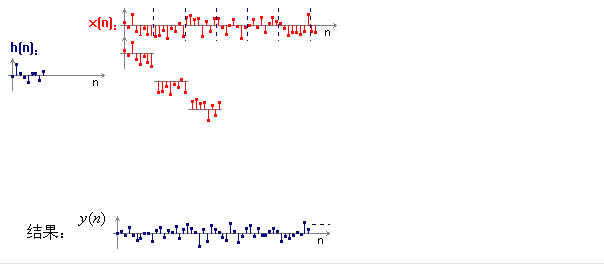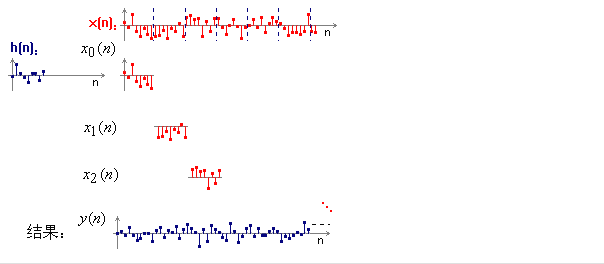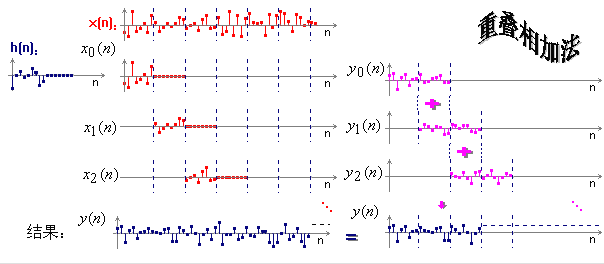
再比如,“欧拉公式”现象。
英国科学期刊《物理世界》曾让读者投票评选了“最伟大的公式”,最终榜上有名的十个公式。有上面说过的傅立叶变换、薛定谔方程和德布罗意方程,无需多言这几个公式中都有exp(ipr)的影子。最神奇的是欧拉公式,似神的启示。
一般人无意间瞟一眼,也许发现不了它的神奇,但对专业人士而言,相信看到它时,都会惊诧到合不拢嘴。高斯曾经说:“一个人第一次看到这个公式而不感到它的魅力,他不可能成为数学家。”
这个公式的巧妙之处在于,它没有任何多余的内容,将数学中最基本的e、i、π放在了同一个式子中,同时加入了数学也是哲学中最重要的0和1,再以简单的加号相连: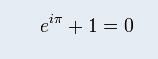
欧拉是历史上最多产的数学家,也是各领域(包含数学的所有分支及力学、光学、音响学、水利、天文、化学、医药等)最多著作的学者。数学史上称十八世纪为“欧拉时代”。欧拉出生于瑞士,31岁丧失了右眼的视力,59岁双眼失明,但他性格乐观,有惊人的记忆力及集中力。他一生谦逊,很少用自己的名字给他发现的东西命名。不过还是命名了一个最重要的一个常数——e
关于e,以前有一个笑话说:在一家精神病院里,有个病患整天对着别人说,“我微分你、我微分你。”也不知为什么,这些病患都有一点简单的微积分概念,总以为有一天自己会像一般多项式函数般,被微分到变成零而消失,因此对他避之不及,然而某天他却遇上了一个不为所动的人,他很意外,而这个人淡淡地对他说,“我是e的x次方。”
e的x次方就是exp(x),在复数域中是exp(ix),如果是二维变量就是exp(ipr)
因为指数函数的微分不变性,所以指数函数成为微分方程的特征解,所以有exp(ipr)是所有线性时不变系统的共同本征函数系。
并且,一眼可见,欧拉公式与exp(ipr)息息相关。从欧拉公式的证明中更可明晰其中端倪:

证明有点稍显复杂,其中核心要点简化如下:


从欧拉公式中我们可以解读到:
1、exp(ipr)中隐含着e、i、π信息。前面提到过e、i、π数据是多维空间的图形结构数据,所以exp(ipr)中隐含着多维空间的图形结构信息,可作张量积扩张。

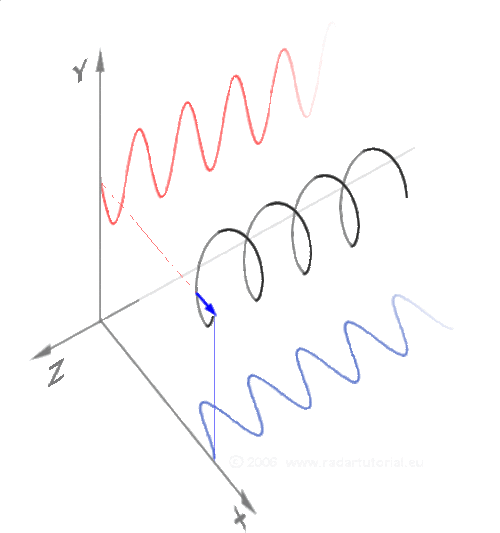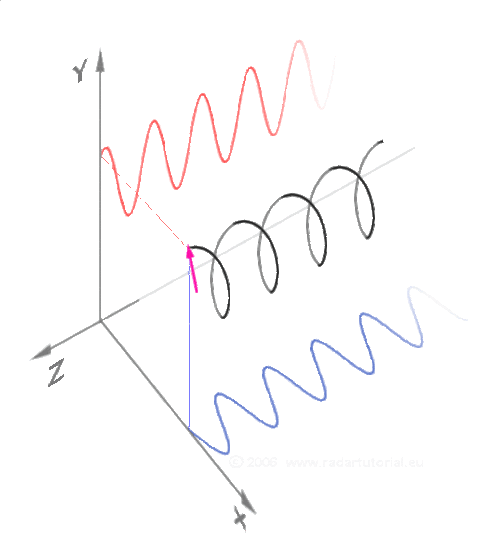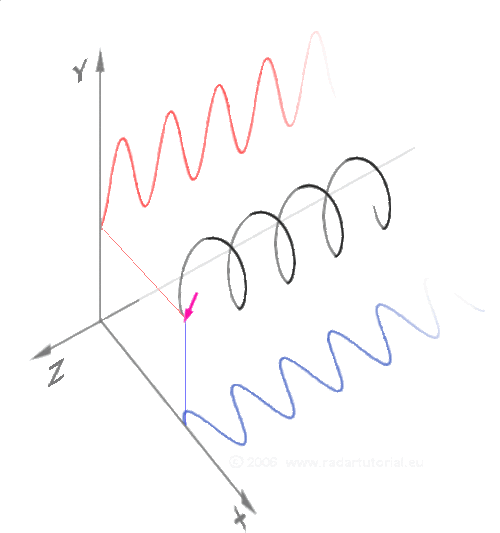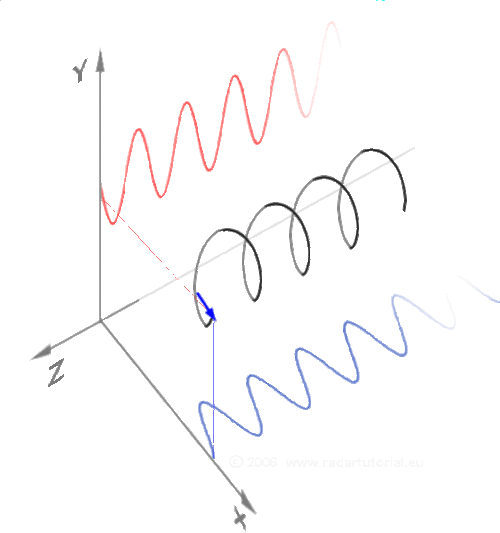
2、exp(ipr) 是sin和cos函数的联合体,而sin、cos同时具备空间周期属性和时间周期属性,所以exp(ipr) 即是频域的本证态、又是时域的本证态。

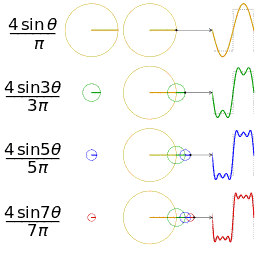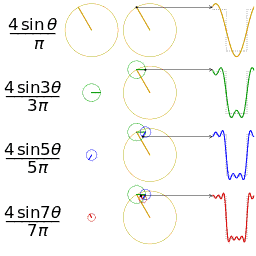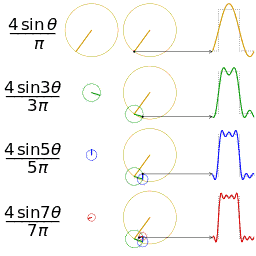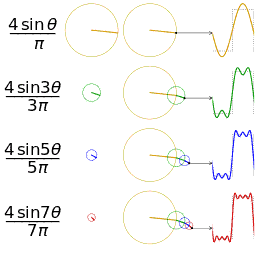
https://wap.sciencenet.cn/blog-1666470-824584.html
上一篇:关于不完备性定理和不确定性原理的探讨(五)(5)
下一篇:关于不完备性定理和不确定性原理的探讨(五)(7)