12.8  这里空白太小写不下

   1637年，有个叫费马的民科在一本书的页边处写几句话：“不可能将一个立方数写成两个立方数之和；或者将一个4次幂写成两个4次幂之和；或者，总的来说，不可能将一个高于2次的幂写成两个同样次幂的和。”

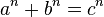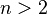   这句话是一个数学算式：     （整数 时不成立）

   这个喜欢恶作剧的天才，又在后面写下一个附加的评注： “我有一个对这个命题的十分美妙的证明，这里空白太小，写不下。”

   初看起来，上面公式似乎太小case了，这不就是勾股定理的高次方吗？

   于是很多人跃跃欲试，更因为有个土豪重金悬赏解题之人，这个简单的公式后来成了大众的热门话题。但是不管是广大业余数学爱好者、或是社会边缘的数学独孤求败，一旦进入这个迷宫，才发现迷雾茫茫、无穷无尽、深不可测。

   开始，费马自己在小册子里写出了4次方的解答。

   然后：

1770年，欧拉证明n=3时定理成立。

1823年，勒让德证明n=5时定理成立。

1839年，拉梅证明n=7时定理成立。

1850年，库默尔证明2<n<100时定理成立。

1955年，范迪维尔以电脑计算证明了2<n<4002时定理成立。

1976年，瓦格斯塔夫以电脑计算证明了2<n<125000时定理成立。

1985年，罗瑟以电脑计算证明了2<n<41000000时定理成立。

1987年，格朗维尔以电脑计算证明了2<n<10^{1800000}时定理成立。

.............

    随着二十世纪计算机技术的进步，不断地有人用计算机来帮助穷举，但毕竟数字是无限的，还是没有找到根本的解决办法。虽然从n等于3到10的18000000次方都证明出来了，不过仍然熊途慢慢。大家都觉得这不是个事啊，因为n可以趋于无穷大，你再怎么努力枚举也无尽头。

    [ 那么，为什么不考虑用一般的数学归纳法论证：当n=m时成立再论n=m+1时同样成立。这种想法从一开始数学家就发现行不通，欧拉在证明3次方时所用的方法和4次方截然不同，因为3次方出现了虚数。由虚数i可知该复空间包含旋量，是高阶张量系统。

     同样不能一般的数学归纳法论证的，是高次方程的解，它也不适用于线性思维。一次方程小学生都会解，二次方程中学生都会解，但是三次方程就不是一般人能解的了——注意数字二和三在这里的差别。对于三次和四次方程，拉格朗日还可以将它们通过降次的方法来解除，也就是四次方程降为三次，三次方程降为两次来解答。但是当把完全相同的过程运用到五次方程时，意外发生了。方程不但没有降为四次，反倒掉头升为了六次方程。拉格朗日的方法在五次方程上遭到了彻底的失败，他到死也没能解决这个问题，最后只能聊以自慰自己还算在数学的其他领域取得了一些声望。前赴后继的数学王子高斯证明了n次方程有n个解，也就是说，五次方程应该有五个解，但是他也没有办法把它们找出来。意大利人鲁菲尼随后索性证明了，如果只使用加减乘除和开方运算的话，一般五次方程是不可能通过一个公式解出的，但是还没有排除更复杂的运算方式。不过这个证明已经很神奇地揭示了一般的代数规律在数字五面前发生了惊人的质变，经典的数学法则到了这里就如同经典物理法则到了宇宙发端的奇点一样全部都失效了。我们必须进入另一个未知的世界才能解开五次方程的谜团，科学家们和任何献身创新的人，都总是在不断地给自己出难题，然后自己再来解答的过程中将人类知识和智慧不断推向新的高度的。]

    想到一个小学数学题：

     上面的算式如果采取列举的办法，需要计算512次，很麻烦。在有限的考试时间内，规规矩矩硬算肯定算不了。

     并且，考虑假如把题目改成：

     [选取无穷序列......-15,-13,-11,-9,-7,-5,-3,-1,1,3,5,7,9,11,13,15......，任意三个数相加能不能等于30 呢？ ]

      显然，枚举办法对无穷序列更无能为力，唯一可行的是凭借抽象方法：

       由于： 单数+单数+单数=单数

       所以：任意三个单数相加等于30不成立，是个伪命题。

     类似的，有个叫怀尔斯的数学迷也同样思考能不能凭借抽象思维方法一举攻破费马大定律难题呢？ 核心焦点在于抽象“同构”。

     具体的涉及到谷山-志村猜想：“有理数域上的每条椭圆曲线都有同构的模形式存在。”

  [ E是一个有理数域上的一个椭圆曲线。定义E的方程模p，p是一个素数。除了有限个p值，我们会得到有np个元素的有限域Fp上的一个椭圆曲线E的不变量ap：其中，ap = np − p

ap是个序列。通过傅里叶变换每个模形式也会产生一个数列。如果ap序列和从模形式得到的序列相同，即a_p(E)=a_p(f) ，其中a_p(E)与椭圆曲线E mod p解的个数有关，a_p(f)来自某类称作模形式的全纯函数傅立叶系数，则该椭圆曲线叫做模的。 谷山-志村猜想判断:"所有Q上的椭圆曲线是模的"。]

此前，有人发现费马大定理是谷山-志村猜想的一个特例推论，显示费马大定理与椭圆曲线及模形式的密切关系。怀尔斯在这一特例范围内证明了谷山志村猜想，从而证明了费马大定理。

证明中最重要的是借助了群论的抽象，椭圆曲线上的点全体构成一个加法群， 点与点之间的“加法”运算，如图所示：

    正因为椭圆曲线存在加法结构，所以它包含了很多重要的数论信息。因为椭圆曲线和它的雅可比簇是同构的，所以它上面的“加法”结构实际上来自于它的雅可比簇的自然加法结构。

    其实很早就有人发现费马大定律只需证明n=p（p是奇素数）时成立即可。这里涉及到数论最基本的概念（素数），很多关于素数的结论一证明，合数就搞定了。以费马大定理为例，你证明了n=p，对于n=pm都不用证明了，因为x^p+y^p=z^p不成立，（x^m）^p+（y^m）^p=（z^m）^p肯定不成立嘛。神奇的是，伽罗华群的‘因数分解’也由一串素数p分圆结构组成。前面说过关于最大单群（魔群）的故事，魔群将傅里叶变换和数论，以及弦论连接到一起。同样神奇的，伽罗华群表示将傅里叶变换和数论，以及椭圆曲线、模形式、费马大定理糅合在一起。椭圆曲线属于代数几何领域，模形式属于复变函数领域，本来风马牛不相及八杆子打不到一起的两个不同领域，由群论抽象合而为一。怀尔斯的伟大功绩不仅在于他慧眼识珠不同的领域抽象同构，而且他把这种抽象同构严格证明了。

    怀尔斯的长篇证明中涉及了塞莫群大小的确切上界，相对繁杂。不过一般读者看看简约版本的证明，亦可领会群论在其证明中的意义：https://www.zhihu.com/question/19817376

   丢番图、毕达哥拉斯、费马、热尔曼、柯西、欧拉、希尔伯特、哥德尔、图灵、伽罗瓦、谷山丰、志村五郎、沃尔夫斯凯尔、怀尔斯…… 这些数学史上最伟大的名字，在整个「费马定理大戏」上轮番登场。他们有的奠定了数论基础、有的为提出费马定理铺平道路，有的提出问题却不给解答，有的人尝试了却失败，有的人只能证明部分结论，有的人没有想过证明这个定理却因为自己另一个数学理论创新而成为整个解答的关键，而这个解答却一度被学界不能理解而弃如敝履，有的人在攀登数学高峰的途中逝世，也有的人在面对人生失意决心自尽却因死前无聊看到了这个费马定理而心生兴趣尝试解答最后放弃自杀。整个费马大定理的故事描绘的是人类为了攀登智慧高峰，如何一代一代前赴后继的历程。这不仅仅是一个358年的传奇，更是抽象思维在无穷无尽世界的多重线性异常复杂的高阶张量模型的大放异彩。

    究其根本，在于域扩张是高阶张量结构的基础，而群论在域扩张中如同骨架一般。所以复杂系综特征属性研究中，如同骨架的‘群’分析是核心。基于此，我们有充分理由相信，未来跨越不同领域的通用人工智能不仅仅是“深度学习”，而且还有‘群’骨架特征属性。虽然未来‘群’骨架通用人工智能高智商值得担心，不过好消息是人类也许可以从它‘群’骨架特征中揣摩读懂它的内心深处的心思，而不象现在我们对隐层黑箱知其然不知其所以然。